Решение систем линейных уравнений.
Теорема Кронекера-Капелли
Пусть дана произвольная система m линейных уравнений с n неизвестными

Исчерпывающий ответ на вопрос о совместности этой системы дает теорема Кронекера Капелли.
Теорема 4.1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Примем ее без доказательства.
Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема 4.2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 4.3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Правило решения произвольной системы линейных уравнений
1. Найти ранги основной и расширенной матриц системы. Если r(А) ≠ r( 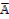 ), то система несовместна.
), то система несовместна.
2. Если r(А) = r( 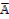 ) = r, система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные n — r неизвестных называют свободными и переносят в правые части уравнений.
) = r, система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные n — r неизвестных называют свободными и переносят в правые части уравнений.
3. Найти выражения главных неизвестных через свободные. Получено общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.
Пример 4.1 . Исследовать на совместность систему

Решение:
A =  , r(A) = 1,
, r(A) = 1,
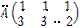 , r(
, r( 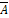 ) = 2
) = 2 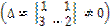
Таким образом, r(А) ≠ r( 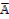 ), следовательно, система несовместна.
), следовательно, система несовместна.
Пример 4. 2. Решить систему
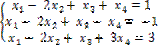
Решение: r(А) = r( 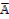 ) = 2. Берем два первых уравнения:
) = 2. Берем два первых уравнения:
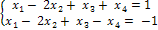
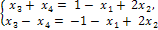
∆ =  = -2 ≠
= -2 ≠
∆1 = 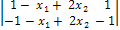 = 2
= 2 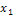 - 4
- 4 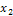
∆1 = 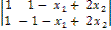 = -2
= -2
Следовательно, х3 = -х1 + 2x2, х4 = 1 — общее решение. Положив, например, x1 = 0, х2 = 0, получаем одно из частных решений: х1 = 0, х2 = 0, х3 = 0, х4 = 1.
Решение невырожденных линейных систем.
Формулы Крамера
Пусть дана система п линейных уравнений с п неизвестными

или в матричной форме А • X = В.
Основная матрица А такой системы квадратная. Определитель этой матрицы . .
∆ = 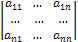
называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.
Найдем решение данной системы уравнений в случае Δ = 0.
Умножив обе части уравнения А • X = В слева на матрицу A-2, получим A-1•А•X = А-1•В.
Поскольку А-1•А = Е и Е • X = X, то
X = A-1 • B
Отыскание решения системы по формуле (4.1) называют матричным способом решения системы.
Матричное равенство (4.1) запишем в виде
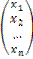 =
= 
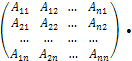
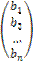 ,
,
то есть
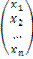 =
= 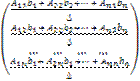
Отсюда следует, что
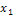 =
= 
……………………………..
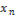 =
= 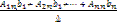
Но А11b1 + А21b2 + … + Аn1bn есть разложение определителя
∆1 = 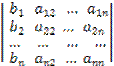
по элементам первого столбца. Определитель Δ1 получается из определителя Δ путем замены первого столбца коэффициентов столбцом из свободных членов.
Итак, x1 = 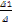
Аналогично: x1 =  где Δ2 получен из Δ путем замены второго столбца коэффициентов столбцом из свободных членов; x3 =
где Δ2 получен из Δ путем замены второго столбца коэффициентов столбцом из свободных членов; x3 =  , … , xn =
, … , xn =  .
.
Формулы
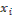 =
=  ,
, 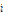 =
= 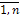
называются формулами Крамера.
Итак, невырожденная система n линейных уравнений с nнеизвестными имеет единственное решение, которое может быть найдено матричным способом (4.1) либо по формулам Крамера (4.2).
Пример 4.3 . Решить систему
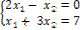
Решение:
∆ = 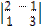 = 7 ≠ 0, ∆1 =
= 7 ≠ 0, ∆1 = 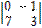 = 7, ∆2 =
= 7, ∆2 = 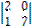 = 14
= 14
Значит, x1 =  = 1, x2 =
= 1, x2 =  = 2
= 2
Дата добавления: 2019-01-14; просмотров: 297; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
