Интегральное исчисление функции»
Цели:
– формирование навыков нахождения неопределенных интегралов методом замены переменной;
– формирование навыков вычисления определенных интегралов методом замены переменной;
– формирование навыков вычисления площади криволинейных фигур с помощью определенного интеграла
Первообразная Неопределенный интеграл и его свойства. Таблица интегралов
| |
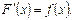 .
.
Свойство первообразной.
Если F1(x) и F2(x) – первообразные для функции f(x) в некотором промежутке Х, то найдется такое число С, что справедливо равенство: 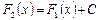 .
Определение. Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается .
Определение. Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается  . .
|
Согласно определению,  .
.
Свойства неопределенного интеграла.
- Производная от неопределенного интеграла равна подынтегральной функции:
 .
. - Дифференциал неопределенного интеграла равен подынтегральному выражению:
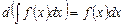 .
. - Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого:
 .
. - Постоянный множитель можно выносить за знак интеграла:
 .
. - Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:
-
 .
.
Таблица интегралов:
 ;
; 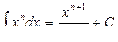 (при п ¹ –1);
(при п ¹ –1); 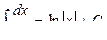 ;
;
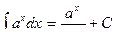 (при а > 0, a ¹ 0);
(при а > 0, a ¹ 0);
|
|
|
 ;
;  ;
;  ;
;
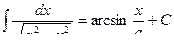 (при
(при 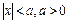 );
);
 (при a ¹ 0);
(при a ¹ 0);
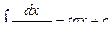
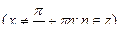 ;
;
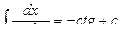
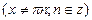 ;
;
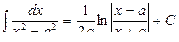 (при a ¹ 0);
(при a ¹ 0); 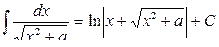 .
.
Приемы интегрирования
Метод непосредственного интегрирования
Метод интегрирования, основанный на применении четвертого и пятого свойств неопределенного интеграла, называется методом разложения или методом непосредственного интегрирования.
Пример. Найдем:
1) 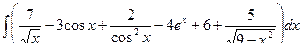 , 2)
, 2) 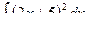 ,
,
3) 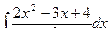 .
.
Решение.
1)Представим интеграл в виде суммы интегралов и, произведя вынесение коэффициентов за знак интеграла, сведем их к табличным:
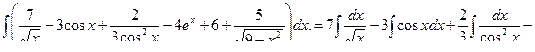
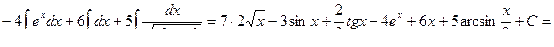
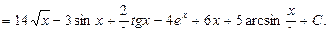
2) Возведя в квадрат подынтегральное выражение, повторим операцию, рассмотренную в предыдущем примере:
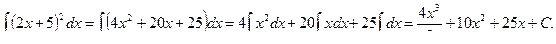
3) Произведя почленное деление подынтегрального выражения на х3, получим:
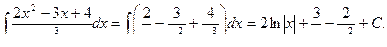
Метод замены переменной
Один из основных методов интегрирования – метод замены переменной (или метод подстановки), описывается следующей формулой:
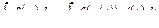 .
.
Однако, новую переменную можно не выписывать явно (в таких случаях говорят о преобразовании функции под знаком дифференциала или о введении постоянных и переменных под знак дифференциала) на основании теоремы:
Теорема. Пусть F(x) – некоторая первообразная для функции f(x). Тогда 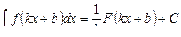 , где k и b – некоторые числа, причем k ¹ 0.
, где k и b – некоторые числа, причем k ¹ 0.
Пример. Найдем 1) 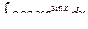 , 2)
, 2) 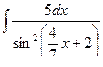
Решение.
|
|
|
1)
|
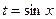 . Тогда
. Тогда 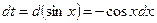
Произведя подстановку, получим:
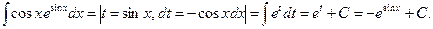
|
2) Так как аргумент подынтегральной функции имеет вид 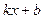 , где
, где 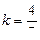 , то, применяя вышеназванную теорему, получим:
, то, применяя вышеназванную теорему, получим:
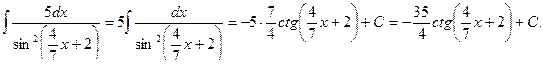
Интегрирование по частям
Формула  называется формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подынтегрального выражения искомого интеграла на два множителя и и dv. При переходе к правой части первый их этих множителей дифференцируется, а второй интегрируется.
называется формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подынтегрального выражения искомого интеграла на два множителя и и dv. При переходе к правой части первый их этих множителей дифференцируется, а второй интегрируется.
Пример. Найдем  .
.
Решение. Применим метод интегрирования по частям.
Положим, что 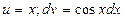 . Тогда
. Тогда 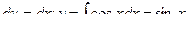 .
.
Подставляя выражения в вышеуказанную формулу, получим:
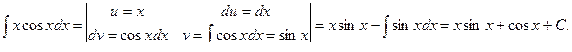
Метод неопределенных коэффициентов
При интегрировании дробно-рациональных функций применяется метод неопределенных коэффициентов. Подынтегральная функция раскладывается на дроби, знаменатели которых представляют собой двучлены первой степени, а числители содержат постоянные: 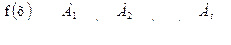 . В качестве элементарной дроби может рассматриваться и дробь следующего вида:
. В качестве элементарной дроби может рассматриваться и дробь следующего вида:  . При этом исходный интеграл сводится к сумме табличных интегралов.
. При этом исходный интеграл сводится к сумме табличных интегралов.
Пример. Найдем 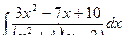 .
.
Решение. Подынтегральная функция разлагается на эламентарные функции вида: 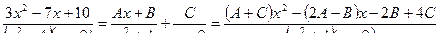 .
.
|
|
|
Приравнивая коэффициенты при равных степенях, получим систему уравнений:
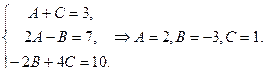
Таким образом, получим:
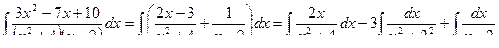
Первый и третий из полученных интегралов решим методом введения новой переменной, приняв в первом случае 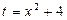 , а во втором
, а во втором 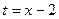 . В итоге получим:
. В итоге получим:
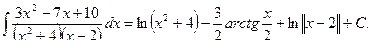
Интегрирование иррациональных функций
Интегралы вида 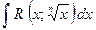 рационализируется заменой переменной
рационализируется заменой переменной 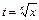 .
.
Интегралы вида 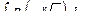 являются частным случаем интегралов от дробно-линейных иррациональностей, т.е. интегралов вида
являются частным случаем интегралов от дробно-линейных иррациональностей, т.е. интегралов вида 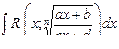 , которые допускают рационализацию посредством замены переменной
, которые допускают рационализацию посредством замены переменной 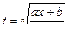 .
.
Пример. Найдем: 1) 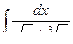 ; 2)
; 2) 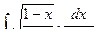 .
.
Решение.
1) Подынтегральная функция содержит радикалы второй и третьей степени. Наименьшее общее кратное равно 6, т. е. данный интеграл рационализируется подстановкой 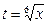 . Тогда
. Тогда 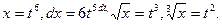 Следовательно, имеем:
Следовательно, имеем:
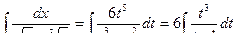
Введите новую переменную, приняв 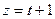 . Проинтегрировав выражение и вернувшись к исходным данным, получим:
. Проинтегрировав выражение и вернувшись к исходным данным, получим:

2) Положим 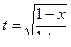 .
.
Тогда  Следовательно,
Следовательно,
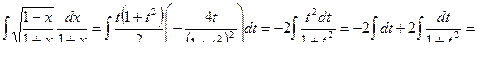
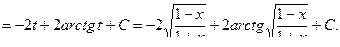
Метод универсальной подстановки
Интегралы от трансцендентных функций вида 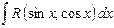 могут быть сведены к интегралам от рациональных функций заменой переменной
могут быть сведены к интегралам от рациональных функций заменой переменной  , где
, где 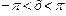 . Тогда, используя выражение синуса и косинуса через тангенс половинного угла и правила дифференцирования, получим:
. Тогда, используя выражение синуса и косинуса через тангенс половинного угла и правила дифференцирования, получим:
|
|
|

| |
 .
.
Решение. Положим 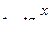 . Используя вышеуказанные замены, найдем:
. Используя вышеуказанные замены, найдем:

Определенный интеграл
Определение. Пусть предел интегральной суммы при стремлении 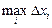 к нулю существует, конечен и не зависит от способа выбора точек х1, х2,… и точек x1, x2,… Тогда этот предел называется определенным интегралом от функции у=f(x) на [a; b], обозначается
к нулю существует, конечен и не зависит от способа выбора точек х1, х2,… и точек x1, x2,… Тогда этот предел называется определенным интегралом от функции у=f(x) на [a; b], обозначается 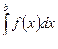 , а сама функция у = f(x) называется интегрируемой на [a; b], т.е.
, а сама функция у = f(x) называется интегрируемой на [a; b], т.е.
 .
.
Свойства определенного интеграла:
1. Постоянный множитель можно выносить за знак интеграла:
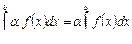 .
.
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: 
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е.
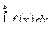

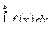 .
.
4. Если на отрезке [a; b] f(x) £ g(x), то и 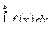 £
£ 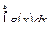 .
.
5. Если функция у = f(x) непрерывна на отрезке [a; b], то найдется такое значение x Î [a; b], что 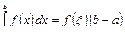 .
.
Формула Ньютона-Лейбница.
Пусть функция у = f(x) непрерывна на отрезке [a; b] и F(x) первообразная функцией для функции f(x) на отрезке [a; b]. Тогда определенный интеграл от функции f(x) на [a; b] равен приращению первообразной на этом отрезке, т.е.  .
.
Пример. Вычислим следующие интегралы:
1) 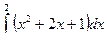 ; 2)
; 2) 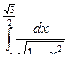 .
.
1) 2) |
Метод замены переменной в определенном интеграле.
Пусть функция 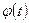 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 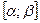 ,
,  ,
, 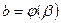 и функция
и функция 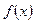 непрерывна в каждой точке вида
непрерывна в каждой точке вида 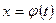 , где
, где 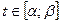 . Тогда справедливо следующее равенство:
. Тогда справедливо следующее равенство: 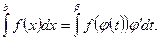
Данная формула называется формулой замены переменной в определенном интеграле. Как видите, использование введения новой переменной в определенном интеграле производится аналогично тому, как это производилось в неопределенном интеграле. Однако в этом случае нет необходимости возвращаться к исходной переменной. Достаточно рассчитать и подставить новые пределы интегрирования.
Пример. Вычислим 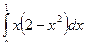 .
.
Решение. Положим 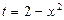 . Тогда
. Тогда  . Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов:
. Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов: 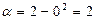 ,
,  . Воспользовавшись формулой замены переменной в определенном интеграле, получим:
. Воспользовавшись формулой замены переменной в определенном интеграле, получим:
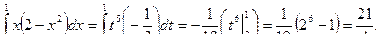
Метод интегрирования по частям в определенном интеграле
Пусть функции  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  . Тогда
. Тогда 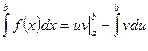 . Эта формула называется формулой интегрирования по частям в определенном интеграле.
. Эта формула называется формулой интегрирования по частям в определенном интеграле.
Пример. Вычислим 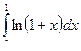 .
.
Решение. Пусть 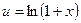 ,
, 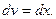
Тогда 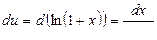 и
и  . Воспользовавшись формулой интегрирования по частям в определенном интеграле, получим:
. Воспользовавшись формулой интегрирования по частям в определенном интеграле, получим:
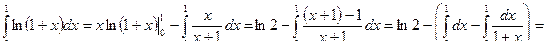
| |
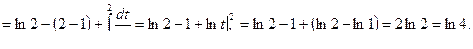
Вы заметили, что при расчете 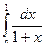 была введена переменная
была введена переменная  .
.
Дата добавления: 2019-01-14; просмотров: 185; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 ;
;