Домашняя на 21 октября: Неравенства
Неравенства, которыми можно пользоваться без доказательства: 
Задача 9. Уравнение 
имеет корень a + b. Доказать, что 
.
Задача 10. 
, если 
.
Задача 11. Найти наименьшее значение выражения 
при положительных x.
Задача 12. Докажите неравенство Коши для четырёх неотрицательных чисел: 
Задача 13. 
, где a, b > 0.
Задача 14 
, где a, b > 0.
Задача 15. Сумма чисел a, b и c равна 0, а их произведение отрицательно. Доказать, что число 
положительно.
Задача 16. Произведение положительных чисел a1, a2, ..., an равно 1. Докажите, что (1 + a1)(1 + a2)...(1 + an) ≥ 2n.
Ссылка на .pdf-версию:
https://www.dropbox.com/s/hnndgxbwt6wyfdr/11%20%D0%BA%D0%BB%D0%B0%D1%81%D1%81%20-%2003%2021.10.pdf?dl=0
Занятие 14 октября: Неравенства
Исходный рубеж
Задача 1.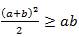 
.
Задача 2.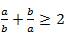 
для любых положительных a и b.
Задача 3.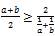 
Основной листок
Задача 1. 
Задача 2. 
, если 
.
Задача 3. 
для положительных a, b.
Задача 4. (a + b)(b + c)(c + a) ≥ 8abc для положительных a, b, c.
Задача 5. 
.
Задача 6. Что больше: 
или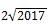 
?
Задача 7. Пусть 
— положительные числа, и 
. Доказать, что 
.
Задача 8. 
Первый листок
Задача 1. , если .
Задача 2.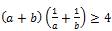 
для положительных a, b.
Задача 3. (a + b)(b + c)(c + a) ≥ 8abc для положительных a, b, c.
Задача 4. .
Задача 5. 
для положительных a, b.
Задача 6. Пусть 
— положительные числа, и 
. Доказать, что 
.
Задача 7. 
Задача 8. Произведение положительных чисел a1, a2, ..., an равно 1. Докажите, что (1 + a1)(1 + a2)...(1 + an) ≥ 2n.
Задача 9. 
Домашняя на 14 октября: Неравенства
|
|
|
Доказать неравенства (для любых действительных переменных, если не указано иное):
Задача 1. 
Задача 2. 
, если .
Задача 3. 
Задача 4. 
Задача 5. Известно, что 
. Доказать, что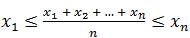 
.
Задача 6. Известно, что 
и 
для всех i. Доказать, что 
.
Задача 7. Известно, что 
. Доказать, что 
.
Задача 8. 
Занятие 7 октября: Неравенства
Доказать неравенства (для любых действительных переменных, если не указано иное):
Задача.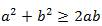 
Задача. 
для любых 
(среднее арифметическое больше либо равно среднего геометрического).
Задача. 
для любых (среднее геометрическое больше либо равно среднего гармонического).
Задача. 
Задача. 
Задача. 
Задача. 
Задача. Известно, что 
. Найти наибольшее возможное значение 
.
Задача. 
для любого натурального k.
Задача. 
Задача. 
Задача. 
Задача. Известно, что 
. Доказать, что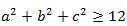 
.
Ссылка на .pdf-версию:
https://www.dropbox.com/s/4felzlu85uu1i7j/11%20%D0%BA%D0%BB%D0%B0%D1%81%D1%81%20-%2002%2007.10.pdf?dl=0
Ссылка на кондуит:
https://docs.google.com/spreadsheets/d/1LVHLkPA9T0UVyfwlHOb6U2SYtKwm_OuN0sW6ez_upmk/
Занятие 30 сентября: регата
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите уравнение: x(x + 1) = 2014*2015.
1.2. Из четырех палочек сложен контур параллелограмма. Обязательно ли из них можно сложить контур треугольника (одна из сторон треугольника складывается из двух палочек)?
|
|
|
1.3. Три пирата нашли клад, состоящий из 240 золотых слитков общей стоимостью 360 долларов. Стоимость каждого слитка известна и выражается целым числом долларов. Может ли оказаться так, что добычу нельзя разделить между пиратами поровну, не переплавляя слитки?
Дата добавления: 2018-11-24; просмотров: 170; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!