Занятие 28 октября: Игры и стратегии

Задача 1. В строчку выписано 100 единиц. Кирилл и Даниил по очереди ставят между какими-нибудь двумя соседними единицами знак плюс или минус. Когда между всеми соседними числами поставлены знаки, вычисляется результат. Если полученное число чётно, то выигрывает Кирилл, в противном случае — Даниил. Кто выиграет, если начинает Кирилл?

Задача 2. Двое красят полоску 1x100. Первый закрашивает по две клеточки подряд, второй — по три клеточки подряд, в произвольном месте ленты. Проигрывает тот, кто не сможет сделать ход. Кто выигрывает при правильной игре? Изменится ли игра, если первый будет закрашивать по три, а второй — по две клеточки?

Задача 3. Имеется шоколадка 6 на 8. За ход разрешается сделать прямолинейный разлом любого куска шоколада вдоль любого из углублений. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

Задача 4. У ромашки а) 14; б) 15 число лепестков. За ход разрешается оторвать любой один или любые два соседних лепестка. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

Задача 5.

a)  На столе лежит 20 комней. За ход можно взять от одного до трёх камней. Проигрывает тот, кто не может сделать ход. Кто из игроков может обеспечить себе выигрыш?

b)  А если конфет 21? А если N?

c)  Тот же вопрос, но взять можно от 2 до 5 камней.

d)  Тот же вопрос, но взять можно 3, 6 или 9 камней.

e)  Тот же вопрос, но взять можно 1, 3 или 4 камня.

Задача 6. Двое играют в такую игру. Они по очереди выкладывают на круглый стол одинаковые монеты. Класть монеты друг на друга нельзя. Проигрывает тот, кому некуда положить очередную монету. Кто из игроков может гарантированно обеспечить себе победу?

Задача 7. В правом нижнем углу шахматной доски стоит хромой король — он может ходить или на клетку влево, или на клетку вверх, или на клетку вверх и влево. Двое игроков по-очереди делают ход королем. Проигрывает тот, кто не может сделать ход. У кого из игроков есть выигрышная стратегия?

 

Домашняя на 28 октября: Неравенства

Напоминаю, что наши основные неравенства:
          

Задача 17.  для положительных a, b.

Задача 18. .

Задача 19. Известно, что ­ . Доказать, что .

Задача 20.  для .

Задача 21. , где .

Задача 22. , где .

Задача 23. Найдите наибольшее значение выражения x²y – y²x, если 0 ≤ x ≤ 1 и 0 ≤ y ≤ 1.

Ссылка на .pdf-версию:

https://www.dropbox.com/s/2b6rwmcq7bd2alm/11%20%D0%BA%D0%BB%D0%B0%D1%81%D1%81%20-%2004%2021.10.pdf?dl=0

Занятие 21 октября: Неравенства

Исходный рубеж

Задача 1.

Задача 2. , где a, b, c > 0.

Задача 3. , где a, b, c > 0.

Листок

Задача 1. Пусть n — натуральное число больше 3. Доказать, что n! ≥ 2ⁿ.

Задача 2. Доказать, что если n – натуральное число больше 1, то .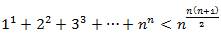

Задача 3. для любых .

Задача 4. , где a, b ≥ 0.

Задача 5. 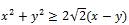, если .

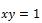Задача 6. , если .

Задача 7. 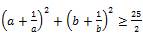, если .

Задача 8. .

Задача 9. Неравенство Коши для трёх неотрицательных чисел: .

---

Дата добавления: 2018-11-24; просмотров: 273; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!