Тема 3. Степінь з натуральним показником
· Поняття про степінь з натуральним показником
· Множення і ділення степенів з однаковими основами
· Степінь добутку та степеня
Виклад теорії
Поняття про степінь з натуральним показником
| Степенем числа a з натуральним показником n, більшим від 1, називають добуток n множників, кожний з яких дорівнює a. Степенем числа a з показником 1 називають саме число a. |
an — степінь з основою a і показником n. Запис «an» читають «a в степені n» або «n-й степінь числа a».
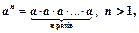a1 = a.
Другий степінь числа a називають квадратом числа a; третій степінь числа a називають кубом числа a.
Приклади.
1. с7 — степінь з основою c і показником 7; читають: «с у сьомому степені» або «сьомий степінь числа c».
2. x2 — степінь з основою x і показником 2; читають: «x у квадраті» або «квадрат числа (виразу, змінної) x».
3. m3 — степінь з основою m і показником 3; читають: «m у кубі» або «куб числа (виразу, змінної) m».
4. За означенням, a5 = a · a · a · a · a; 23 = 2 · 2 · 2 = 8; (a + b)4 = (a + b)(a + b)´
´(a + b)(a + b); (ac)2 = (ac)(ac).
| Натуральний степінь числа 0 дорівнює 0. |
0n = 0.
Приклади.
01 = 0; 02 = 0; 0100 = 0; 01002 = 0.
Натуральним степенем додатного числа є додатне число.
Якщо n — натуральне число, a — додатне, то an — додатне. Дійсно, an =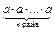 
> 0 як добуток додатних чисел.
Приклади.
1. 53; 
; 0,76; 0,0011001 — додатні числа.
2. Якщо b > 0, то b2 > 0, b5 > 0, b13 > 0, b1002 > 0.
Степінь від’ємного числа з парним показником є додатним числом (як добуток парної кількості від’ємних множників).
|
|
|
Якщо n = 2; 4; 6; 8; …; 2k; …, a — від’ємне, то an — додатне число.
Приклади.
1. (–5)2;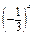 
; (–0,002)8; 
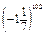— додатні числа.
2. Якщо x < 0, то x2 > 0, x4 > 0, x10 > 0, x104 > 0.
Степінь від’ємного числа з непарним показником є від’ємним числом (як добуток непарної кількості від’ємних множників).
Якщо n = 1; 3; 5; 7; …; 2k + 1; …, a — від’ємне, то an — від’ємне число.
Приклади.
1. (–5)3;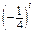 
; (–0,56)7; (–0,001)1001 — від’ємні числа.
2. Якщо x < 0, то x3 < 0, x5 < 0, x11 < 0, x1003 < 0.
| Дію знаходження степеняназивають піднесенням до степеня. | |
| Піднесення до степеня називають дією третього ступеня. Множення і ділення — дії другого ступеня; додавання і віднімання — дії першого ступеня. |
Приклади.
1. Піднести до квадрата:
32 = 3 · 3 = 9;
(–5)2 = (–5) · (–5) = 25;
0,52 = 0,5 · 0,5 = 0,25;
= 
· = 
;
= 
= 
· = 
= 
.
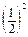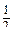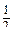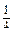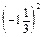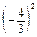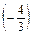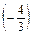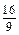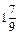2. Піднести до куба:
53 = 5 · 5 · 5 = 125;
(–5)3 = (–5) · (–5) · (–5) = –125;
0,13 = 0,1 · 0,1 · 0,1 = 0,001;
= · · = 
;
= 
= 
· · = 
= 
.
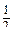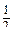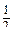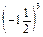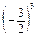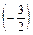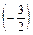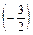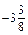3. Піднести до степеня:
24 = 2 · 2 · 2 · 2 = 16;
(–10)4 = (–10) · (–10) · (–10) · (–10) = 10000;
(–0,1)4 = (–0,1) · (–0,1) · (–0,1) · (–0,1) = 0,0001;
= 
· 
· · · = 
.
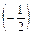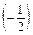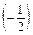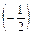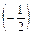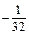Якщо вираз містить дії різних ступенів, то виконують:
· спочатку дії третього ступеня;
· потім дії другого ступеня;
|
|
|
· останніми дії першого ступеня.
Якщо вираз містить дужки, то спочатку виконують дії у дужках.
Приклади.
1. 2 + 7 · 23 = 2 + 7 · 8 = 2 + 56 = 58.
2. 32 + 42 = 9 + 16 = 25.
3. (3 + 4)2 = 72 = 49.
4. 50 – (2 + 5)2 = 50 – 72 = 50 – 49 = 1.
| У процесі словесного читання виразів, які містять степені, дотримують загального правила: |
· першою називають дію, яку виконують останньою.
Приклади.
1. a2 + b2 — сума квадратів чисел (виразів) a та b.
2. a3 – b3 — різниця кубів чисел (виразів) a та b.
3. (a + m)2 — квадрат суми чисел (виразів) a та m.
4. (x – 5)3 — куб різниці чисел (виразів) x та 5.
Дії зі степенями
Множення і ділення степенів з однаковими основами
| Теорема. Добуток степенів будь-якого числа a з показниками m і n дорівнює степеню числа a з показником m + n: |
am · an = am+n.
Щоб помножити степені з однаковими основами, потрібно:
· основу залишити без зміни;
· показники степенів додати.
Приклади.
1. a5 · a8 = a13; b4 · b10 = b14.
2. 74 · 78 = 712;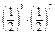 
= 
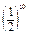; 0,150 · 0,120 = 0,170; 
.
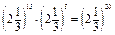Доведення теореми
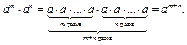
Ілюстрація доведення
| Теорема. Частка степенів будь-якого числа a ¹ 0 з показниками m і n такими, що m > n, дорівнює степеню числа a з показником m – n: |
am : an = am–n.
Щоб поділити степені з однаковими основами, потрібно:
|
|
|
· основу залишити без зміни;
· від показника діленого відняти показник дільника.
Приклади.
1. a8 : a5 = a3; b10 : b2 = b8.
|
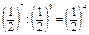; 0,150 : 0,120 = 0,130; 
.
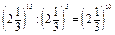Доведення теореми
1. am–n · an = am–n+n = am.
2. Оскільки am–n · an = am, то за означенням ділене am–n є часткою чисел am : an, тобто am : aт = am–n.
Ілюстрація доведення
Оскільки a7 · a3 = a10 за властивістю добутків степенів, то за означенням частки a10 : a7 = a3.
Степінь добутку та степеня
| Теорема. Для будь-яких чисел a і b n-й степінь їх добутку дорівнює добутку n-х степенів цих чисел: |
(a · b)n = an · bn.
Щоб піднести до степеня добуток, можна піднести до цього степеня кожний множник і результати перемножити:
(abc)n = an · bn · cn; (abcd)n = an · bn · cn · dn.
Приклади.
(ax)3 = a3 · x3; (5a)2 = 52 · a2 = 25a2; (10ab)4 = 104 ·a4 · b4 = 10000a4b4; (2ab)3 = 23 · a3 · b3 = 8a3b3.
Доведення теореми
Ілюстрація доведення
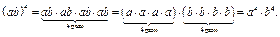
| Теорема. Для будь-якого числа a і довільних чисел m і n справедлива рівність: |
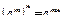
Дата добавления: 2018-10-27; просмотров: 377; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!