Лекция 15. Преобразование сигналов в линейных и нелинейных каналах связи
Содержание лекции:
- переходные и частотные характеристики линейных стационарных систем.Условие физической реализуемости. Спектральный метод. Преобразование случайных сигналов в детерминированных линейных каналах.Воздействие стационарных случайных сигналов на безынерционные нелинейные цепи. Прохождение случайных сигналов с широким спектром через узкополосные цепи.
Цель лекции:
- Систематическое решение задач о прохождении разнообразных сигналов через линейные системы. Показать применение спектрального подхода как к задаче нахождения реакции системы, так и к проблеме числовой оценки выходного сигнала. Исследовать ту связь между статистическими характеристиками процессов X(t) и Y(t), которая может быть найдена на основе математической модели системы.
Физически реализуемая система должна быть, кроме того, устойчивой. Это означает, что ее импульсная характеристика должна удовлетворять условию абсолютной интегрируемости
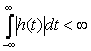. (15.1)
Пусть на входе линейной стационарной системы действует сигнал, изображаемый функцией Хевисайда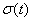 
.Выходную реакцию
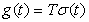(15.2)
принято называть переходной характеристикойсистемы.
Поскольку система стационарна, переходная характеристика инвариантна относительно временного сдвига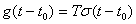 
.
Переходная характеристика физически реализуемой системы отлична от нуля лишь при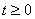 
, в то время, как g (t) = 0 при t < 0.
|
|
|
Между импульсной и переходной характеристиками имеется тесная связь. Действительно, так как δ(t)=dσ/dt, то на основании (14.6)
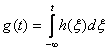. (15.3)
Покажем, что комплексный сигнал uвх(t) =exp (jωt) при любом значении частоты ω есть собственная функция cтaциoнaрнoгo оператора. Для этого воспользуемся интегралом Дюамеля вида (14.8) и вычислим
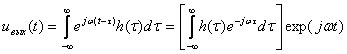. (15.4)
Отсюда видно, что собственным значением системного оператора является комплексное число
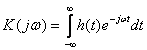, (15.5)
называемое частотным коэффициентом передачи системы.
Формула (15.5) устанавливает принципиально важный факт — частотный коэффициент передачи и импульсная характеристика линейной стационарной системы связаны между собой преобразованием Фурье. Поэтому всегда, зная функцию K ( jω ),можно определить импульсную характеристику
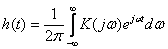. (15.6)
Важнейшее положение теории линейных стационарных систем - любую такую систему можно рассматривать либо во временной области с помощью ее импульсной или переходной характеристик, либо в частотной области, задавая частотный коэффициент передачи. Оба подхода равноценны, и выбор одного из них диктуется удобствами получения исходных данных о системе и простотой вычислений.
Часто пользуются представлением частотного коэффициента передачи в показательной форме
|
|
|
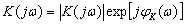. (15.7)
Обе входящие сюда вещественные функции носят специальные названия: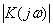 
— амплитудно-частотная характеристика(АЧХ), φK(ω) - фазочастотная характеристика (ФЧХ) системы.
Далеко не каждая функция К ( jω ) может являться частотным коэффициентом передачи физически реализуемой системы. Простейшее ограничениесвязано с тем, что импульсная характеристикаh ( t ) такой системы обязана быть вещественной
K ( jω )= K * (- jω ). (15.8)
В соответствии с формулой (10.13) модуль частотного коэффициента передачи (АЧХ) есть четная, а фазовый угол (ФЧХ) — нечетная функция частоты.
Каким должен быть частотный коэффициент передачи для того, чтобы выполнялись условия физической реализуемости (14.9) и (15.1). Приведем без доказательства окончательный результат, известный под названием критерия Пэли — Винера: частотный коэффициент передачи физически реализуемой системы должен быть таким, чтобы существовал интеграл
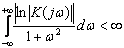. (15.9)
Спектральный метод анализа прохождения радиотехнических сигналов через линейные стационарные системы - целый комплекс математических приемов, в основе которых лежит использование свойств частотного коэффициента передачи системы.
|
|
|
. (15.10)
Этоосновная формуласпектрального метода, свидетельствующая о том, что частотный коэффициент передачи системы служит множителем пропорциональности между спектральными плотностями сигналов на входе и выходе:
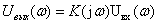. (15.11)
Исследование преобразований случайных процессов при их прохождении через линейные динамические системы (как с регулярными, так и со случайно меняющимися параметрами) связано с решением задач двух типов: определение корреляционной функции (спектральной плотности мощности) отклика Y ( t ) на выходе системы, заданной своими характеристиками, по данной корреляционной функции (или спектральной плотности мощности) входного воздействия X ( t )определение многомерного распределения вероятностей отклика У( t ) на выходе системы по многомерному распределению входного воздействия X ( t ).
В стационарной детерминированной линейной системе с финитной, т.е. ограниченной во времени пределами 0...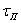 
ИХ g ( t ) отклик
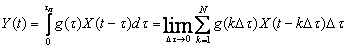. (15.12)
Шаг дискретизации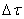 
можно выбрать равным интервалу корреляции входного процесса 1/Fx. Допустим, что входной процесс центрирован 
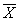( t )=0, тогда центрирован и выходной процесс. Узкая полоса пропускания 
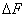означает, что длительность импульсной характеристики τ велика по сравнению с 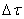. Сечение выходного процесса Y ( t ) в любой момент времени tопределяется согласно (15.12) Nслагаемыми суммы. В эту сумму входит много некоррелированных между собой сечений процесса X ( t ).Распределение вероятностей такой суммы согласно центральной предельной теореме теории вероятности близко к гауссовскому (тем ближе, чем больше N ,определяемое отношением Fx /∆ F ). В предельном случае, если на вход канала воздействует белый шум, у которого ширина спектра бесконечна (не совпадающие во времени отсчёты не коррелированы), а канал имеет ограниченную полосу пропускания, то N 
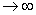и выходной процесс будет строго гауссовским. Отмеченное свойство линейного канала сохраняется и при изменении параметров канала.
|
|
|
ФК выходного стационарного процесса Y ( t )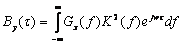 
.
Предположим, что на входе безынерционной нелинейной системы присутствует случайный сигнал x ( t ), являющийся одной из реализаций стационарного случайного процесса X ( t ).Выходной сигнал y ( t ) связан с входным воздействием зависимостью вида y { t )= f [ x { t )];ансамбль реализаций y { t ) задает стационарный случайный процесс Y(t), Ставится задача найти связь между статистическими характеристиками процессов X ( t ) и Y ( t ). При этом возможны два частных подхода:
1) По известной и-мерной плотности вероятности входного случайного процесса рвх(х1, х2,...,х n ; tl , t 2 ,..., tn ) ищут аналогичную функцию рвых(y1, y2 ,..., yn ; tl , t 2 ,..., tn )определяющую выходной сигнал.
2) Исследование проводят в рамках корреляционной теории — ищут математическое ожидание ту и функцию корреляции Ry ( t )выходного случайного процесса. Наряду с функцией корреляции интерес может представлять спектральная плотность мощности Wy(w) выходного сигнала.
Если x1, x2, ..-, х n — случайные значения, наблюдаемые на входе в моменты времени t1, t 2 ,..., tn соответственно, то, учитывая безынерционный характер преобразования, имеем на выходе в те же моменты времени
y1=f(x1), y2=f(x2),…, yn=f(xn). (15.13)
Применив обратную функцию x = g ( y ),получим
x1=g(y1), х 2 =g(y2),.., х n=g(yn). (15.14)
Тогда многомерная плотность вероятности на выходе
рвых(y1, y2 ,..., yn =рвх[g(y1), g ( y 2 ),..,g(yn)]½D½, (15.15)
где D — якобиан преобразования функции (15.13).
Формула (15.15) решает поставленную задачу в самом общем виде.
Простейшая статистическая характеристика стационарного случайного процесса — его среднее значение, получающееся путем усреднения по ансамблю реализаций. Чтобы вычислить среднее значение сигнала после нелинейного безынерционного преобразования, нужно располагать одномерной плотностью вероятности pвых(y). На основании принципа усреднения
my = (15.16)
Спектр колебаний на выходе нелинейного преобразователяразбивается на бесконечную сумму составляющих, каждая из которых отображает индивидуальный узкополосный случайный процесс. Максимумы спектральных плотностей мощности этих составляющих наблюдаются на частотах nwо. Помимо этого в спектре выходного сигнала возникает низкочастотная составляющая в окрестности нулевой частоты, которую можно рассматривать как результат амплитудного детектирования входного сигнала. При различных видах характеристики нелинейного элемента можно ожидать появления тех или иных гармоник центральной частоты входного случайного колебания.
Часто приходится рассматривать воздействие на линейные частотно-избирательные цепи широкополосных случайных сигналов, образованных, например, хаотической последовательностью коротких импульсов. В этом случае если эффективная ширина спектра входного случайного процесса значительно превышает ширину полосы пропускания системы, то реальный случайный процесс можно заменить эквивалентным ему белым шумом с односторонним спектром мощности N0 =Nx (f0), где f 0 ~некоторая точка в пределах полосы пропускания.
Дата добавления: 2018-09-20; просмотров: 450; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!