Лекция 11. Классификация помехоустойчивых кодов. Циклические коды

Содержание лекции:

-классификация помехоустойчивых кодов. Циклические коды. Обнаружение ошибок при циклическом кодировании. Определение места ошибки. Выбор образующего полинома.

Цель лекции:

- получить знания основ помехоустойчивого кодирования.

Помехоустойчивые коды (см. рисунок 11.1) делятся на блочные и непрерывные. К блочным относятся коды, в которых каждому сообщению соответствует блок из п символов (разрядов) или блоки с разным числом символов. Непрерывные коды, к которым относятся рекуррентные (называемые также сверточными), представляют собой непрерывные последовательности единичных элементов, не разделенные на блоки. В таких кодах избыточные разряды помещаются в определенном порядке между информационными. В разделимых кодах элементы информационной и проверочной частей кодовой комбинации всегда стоят на определенных местах. В неразделимых кодах деление на информационные и проверочные разряды отсутствует. К таким кодам относится код с постоянным весом. Код называется линейным, если любая разрешенная кодовая комбинация может быть получена в результате линейной операции над набором k ненулевых линейно-независимых кодовых комбинаций. В систематических кодах проверочные элементы формируются линейным преобразованием информационных.

Циклические коды относятся к классу линейных систематических кодов и обладают всеми их свойствами. Удобно рассматривать кодовые комбинации циклического кода не в виде последовательности нулей и единиц, а в виде полинома некоторой степени. Любое число в любой системе счисления можно представить в общем виде как

, (11.1)

где х — основание системы счисления; a_i - цифры данной системы счисления; п-1, п-2,... — показатель степени, в которую возводится основание, и одновременно порядковые номера, которые занимают разряды, начиная от старшего, кончая нулевым. Для двоичной системы х=2, а a_iлибо «0», либо «1».

Очевидно, что при записи кодовой комбинации в виде многочлена единица в 1-м разряде записывается членом , а нуль вообще не записывается. Представление кодовых многочленов позволяет установить однозначное соответствие между ними и свести действия над комбинациями к действию над многочленами. Так, сложение двоичных многочленов сводится к сложению по модулю 2 коэффициентов при равных степенях переменной x. Например,

Умножение производится по обычному правилу умножения степенных функций, однако полученные коэффициенты при данной степени складываются по модулю 2.

Например,

Деление также осуществляется, как обычное деление многочленов; при этом операция вычитания заменяется операцией сложения по модулю 2*:

Коды названы циклическими потому, что циклический сдвиг а _n _-2, а _n _-3,…, а_2,а_1,а_0,а _n _-1разрешенной комбинации а _n _-1, а _n _-2,…, а_2,а_1,а₀также является разрешенной комбинацией. Такая циклическая перестановка при использовании представления в виде полиномов появляется в результате умножения данного полинома на х. Если , то Чтобы степень многочлена не превышала n -1, член заменяется единицей, поэтому

Например, имеем кодовую комбинацию Сдвинем ее на один разряд. Получим

Очевидно, что

Теория построения циклических кодов базируется на разделах высшей алгебры, изучающей свойства двоичных многочленов. Особую роль в этой теории играют так называемые неприводимыемногочлены, т.е. полиномы, которые не могут быть представлены в виде произведения многочленов низших степеней. Такой многочлен делится только на самого себя и на единицу. Из высшей алгебры известно, что на неприводимый многочлен делится без остатка двучлен х^п+1. В теории кодирования неприводимые многочлены называются образующими полиномами, поскольку они «образуют» разрешенные кодовые комбинации.

Идея построения циклического кода сводится к тому, что полином, представляющий информационную часть кодовой комбинации, нужно преобразовать в полином степени не более п—1, который без остатка делится на образующий полином Р(х). Существенно при этом, что степень последнего соответствует числу разрядов проверочной части кодовой комбинации. В циклических кодах проверочная часть получается сразу, т. е. используется алгоритм .Тогда все разрешенные комбинации циклического кода, представленные в виде полиномов, будут обладать одним признаком: делимостью без остатка на образующий полином Р(х). Построение разрешенной кодовой комбинации сводится к следующему:

1)Представляем информационную часть кодовой комбинации длиной k в виде полинома Q (х).

2) Умножаем Q (х) на одночлен х ^r и получаем Q (х)х ^r , т. е. производим сдвиг k-разрядной кодовой комбинации на г разрядов.

3) Делим многочлен Q (х)х ^rна образующий полином Р(х), степень которого равна r .

В результате умножения Q (х)на х ^r степень каждого одночлена, входящего в Q (х), повышается на r . При делении произведениях ^r Q (х) на образующий полином степени rполучается частное С(х) такой же степени, что и Q (х). Результаты этих операций можно представить в виде

где R (х) — остаток от деления Q (х)х ^r на Р(х). Поскольку С(х) имеет такую же степень, что и Q (х), то С(х) представляет собой кодовую комбинацию того же k-разрядного кода. Степень остатка не может быть, очевидно, больше степени образующего полинома, т. е. его наивысшая степень равна r —1. Следовательно, наибольшее число разрядов остатка не превышает r .Умножив обе части (6.18) на Р(х), получим

F (х) = С(х)Р(х) = Q (х)х ^r + R (х) (11.2)

(знак вычитания заменяется знаком сложения по модулю 2). Очевидно, что F (х)делится на Р(х) без остатка. Полином F (х)представляет собой разрешенную кодовую комбинацию циклического кода. Из (11.2) следует, что разрешенную кодовую комбинацию циклического кода можно получить умножением кодовой комбинации Q (х) простого кода на одночлен х ^r и добавлением к этому произведению остатка R (х), полученного в результате деления произведения на образующий полином Р(х).

Обнаружение ошибок при циклическом кодированиисводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался при кодировании (вид его, разумеется, должен быть известен на приеме). Если ошибок в принятой кодовой комбинации нет (или они такие, что данную передаваемую кодовую комбинацию превращают в другую разрешенную), то деление на образующий полином произведется без остатка. Если при делении получится остаток, то это и свидетельствует о наличии ошибки. Остаток от деления в циклических кодах играет роль синдрома. Остаток от деления — синдром циклического кода, не равный нулю, — свидетельствует о наличии ошибки.В кодах с образующим полиномом степени г остаток представляется в виде полинома, степень которого меньше r. Это означает, что количество различных ненулевых остатков может быть равным . Номер разряда, в котором произошла ошибка, однозначно связан с видом получающегося при этом ненулевого остатка. Это позволяет по виду синдрома (остатка) определить место ошибки. Таким образом, для исправления ошибокнеобходимо обеспечить условие, при котором количество различных ненулевых остатков будет равно количеству элементов п (при исправлении одной, ошибки) или числу комбинаций из п по t _и , где t _и— количество ошибок, исправляемых кодом. Следует подчеркнуть, что не все неприводимые многочлены позволяют формировать 2^r—1 различных остатков. Это присуще только определенному классу многочленов, которые именуются «примитивными». Так, 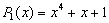удовлетворяет указанному требованию, а— нет, т. е. —примитивный многочлен. Исходя из приведенных соображений, в качестве образующих многочленов используют примитивные многочлены. Их признаком является наличие остатка, равного единице только для х° и х^п, где п — количество элементов в кодовой комбинации. Между n и r для таких полиномов имеется зависимость 2 ^r =п—1. Здесь п — максимальное количество элементов, при котором число различающихся ненулевых остатков равно п—1. Поэтому в таблицах образующих полиномов указываются только примитивные полиномы.

Для определения места ошибки в циклическом коде существует несколько методов, основанных на анализе синдрома Р(х). Принятую кодовую комбинацию F '(х)можно представить в виде , где Е (х) —многочлен ошибки. Остаток от деления принятой кодовой комбинации F '_п(х)на Р(х) равен остатку от деления на Р(х) кодовой комбинации ошибки Е_п(х), если F _п (х) = F '_п(х) Е_п(х). Это условие справедливо, если код способен исправлять количество ошибок t_и, равное или меньшее веса комбинации Е_п(0,1). На основе этого свойства можно заключить, что синдром не зависит от переданной кодовой комбинации, а определяется лишь наличием ошибок. Указанное свойство можно использовать для определения ошибочно принятого элемента. Предположим, что ошибка произошла в старшем разряде переданной кодовой комбинации a _1. В этом случае R ₁ (х) - есть остаток от деления принятой комбинации F _п (х)на Р(х). Такой же остаток R ₁ (х) получается, если разделить на Р(х)комбинацию ошибки, т. е. многочлен х^п-¹. Но такой же остаток получится при ошибке в разряде а₂, еслиF ^/ _п (х) умножить на х. То же будет и при ошибке в разряде а₃, если F _п (х) умножить на х², и т. д.

Дата добавления: 2018-09-20; просмотров: 535; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!