Мгновенная частота ФМ колебания
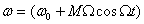. (6.6)
Таким образом, ФМ колебание в разные моменты времени имеет различные мгновенные частоты, отличающиеся от частоты несущего колебания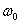 
на величину 
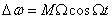, что позволяет рассматривать ФМ колебание как модулированное по частоте.
Наибольшее отклонение частоты ω от ω0 называется девиацией частоты∆ωД. Согласно (6.6)
∆ωд = MΩ или ∆f Д = MF . (6.7)
Частотная модуляциязаключается в пропорциональном первичному сигналуx ( t ) изменении мгновенной частоты переносчика
ω=ω0+ax ( t ), (6.8)
где а —коэффициент пропорциональности. Мгновенная фаза ЧМ колебания: 
.
Аналитическое выражение ЧМ колебания с учетом постоянства амплитуды можно записать в виде: 
. (6.9)
В простейшем случае модуляции гармоническим колебанием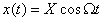 
мгновенная частота 
,где 
—девиация частоты, т. е. максимальное ее отклонение от несущей частоты ω0, вызванное модуляцией. Аналитическое выражение этого ЧМ колебания согласно (6.9)
.
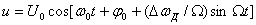Слагаемое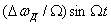 
характеризует изменение фазы, получающееся при ЧМ. Это позволяет рассматривать ЧМ колебание как ФМ колебание с индексом модуляции
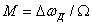, (6.10)
и записать его аналогично (8.9)
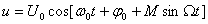. (6.11)
Из сказанного следует, что ФМ и ЧМ колебания имеют много общего. Так колебание вида (8.11) может быть результатом как ФМ, так и ЧМ гармоническим первичным сигналом. Кроме того, ФМ и ЧМ характеризуются одними и теми же параметрами (индексом модуляции М и девиацией частоты ∆ f Д), связанными между собой одинаковыми соотношениями: (6.7) и (6.10).
|
|
|
Наряду с отмеченным сходством частотной и фазовой модуляции между ними имеется и существенное отличие, связанное с различным характером зависимости величин М и ∆ f Д от частоты F первичного сигнала:
- при ФМ индекс модуляции не зависит от частоты F, а девиация частоты согласно (1.23) пропорциональна F;
|
- при ЧМ девиация частоты не зависит от частоты F, а индекс модуляции согласно (6.10) обратно пропорционаленF.
Различие между частотной и фазовой модуляцией особенно заметно, когда модуляция производится сложным сигналом, содержащим большое число компонент с разными частотами. Для иллюстрации сказанного на рисунках 6.2 б,в построены графики ЧМ и ФМ колебаний, соответствующие сигналу x ( t )треугольной формы (см. рисунок 6.2 а). При ЧМ увеличение x ( t )сопровождается возрастанием w и наоборот. При ФМ ∆φ(t) = ax ( t ),a ω= ω0+ adx / dt .Поэтому на участках, где dx / dt >0,мгновенная частота ω больше несущей на величину 
; на участках сdx / dt < 0 частота ФМ колебания меньше ω0 на величину ∆ω. Таким образом, ФМ сигналом x ( t )треугольной формы совпадает с ЧМ сигналом x 1 ( t ) (см. рисунок 8.2 г) прямоугольной формы. И вообще любое-колебание с угловой модуляцией может быть получено как в результате ФМ первичным сигналом x ( t ), так и ЧМ первичным сигналом х1( t )= dx / dt . К сказанному следует добавить, что частотная и фазовая модуляция различаются также способами их осуществления.
|
|
|
Исходным для определения спектровколебаний при гармонической угловой модуляции является выражение (6.11). Примем для упрощения выражений φ0=0 и перепишем (6.11) в виде
. (6.12)
Выражение (6.12) представляет сумму двух квадратурных колебаний частоты ω0, из которых каждое модулировано по амплитуде частотой Ω. Угловую модуляцию принято подразделять на узкополосную (М<0,5 рад) и широкополосную (M>0,5рад). Наибольшее распространение в технике связи имеет широкополосная ЧМ с М>>1.Начнем с определения спектра узкополосной угловой модуляции. Полагая M << l, имеем
, (6.13)
а потому
. (6.14)
Таким образом, спектр узкополосных сигналов угловой модуляции аналогичен спектру простейшего AMколебания, показанному на рисунке 5.2. Он содержит компоненты несущей частоты ω0 и двух боковых частот ω0+Ω и ω0−Ω. Параметром, определяющим амплитуды боковых частот, здесь является индекс модуляции М. Ширина спектра узкополосной угловой модуляции такая же, как и при AM: она равна удвоенной частоте модуляции. Несмотря на идентичность спектров, рассматриваемое колебание отличается от AMколебания, что является следствием различия в знаках (т. е. в сдвиге фаз на 180°) компонент нижней боковой частоты в выражениях (6.14) и (5.5). Это означает возможность преобразования AM колебания в узкополосное ФМ колебание поворотом фазы одной из боковых частот на 180°.
|
|
|
При широкополосной угловой модуляции M >> 1 выражения (5.5) и (6.14) несправедливы. Приходится спектр колебаний определять непосредственно из (6.12). Выражения 
и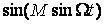 
являются периодическими функциями частоты, а потому они могут быть разложены в ряды Фурье. Первая из этих функций является четной, вторая—нечетной.
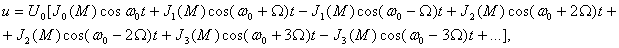
где Jn ( M ) — функция Бесселя первого рода п-гопорядка от аргумента М.Таким образом, спектр ЧМ и ФМ колебаний, модулированных гармоническим сигналом, оказывается дискретным, симметричным относительно ω0 и содержащим бесконечное число боковых частота вида ω0±nΩ с амплитудами An = U 0 Jn ( M ). Для М=4 он построен на рисунке 6.3. При ограничении спектра необходимо учитывать влияние двух противоречивых факторов: в более узкой полосе частот ослабляется влияние помех, но одновременно увеличиваются искажения сигнала из-за отсутствия опускаемых составляющих. На практике выбирают компромиссное решение. Отличие ширины спектра сигналов гармонической угловой модуляции от интервала частот2∆ fд, в пределах которого происходит изменение мгновенной частоты сигнала:
|
|
|
а) теоретическая ширина спектра ∆ f чм, фм=∞;
б) практическое ее значение при М<<1 оказывается ∆ f чм, фм=2F>>2∆ fд, а при M >>1 ∆ f чм, фм несколько превышает 2∆ fд и лишь приближенно считается равной ей (8.17). Рассмотрим влияние параметров модулирующего сигнала x ( t )= XcosΩt на спектры ФМ и ЧМ колебаний, используя (8.17). При изменении амплитуды Хмодулирующего сигнала спектры ФМ и ЧМ колебаний изменяются одинаково. При возрастании Х происходит пропорциональное увеличение индекса модуляции, спектры расширяются за счет увеличения числа спектральных компонент. Изменение частоты Fмодулирующего колебания по-разному влияет на изменение спектров ФМ и ЧМ колебаний. При ФМ изменение F не влияет на величину индекса модуляции, а следовательно, и на число спектральных составляющих (см. рисунки 6.4 а, б).
При ЧМ с уменьшением Fиндекс модуляции увеличивается, что приводит к увеличению числа спектральных компонент (см. рисунки 6.4 в, г). В итоге ширина спектра ЧМ колебания от частоты почти не зависит, а при ФМ изменяется пропорционально F.
Дата добавления: 2018-09-20; просмотров: 744; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!