Лекция 4. Динамическое представление сигналов. Дискретизация сигналов во времени

Содержание лекции:

- принцип динамического представления. Представление непрерывной функции дискретной последовательностью отсчётов её мгновенных значений. Спектральная трактовка дискретизации. Теорема отсчётов. Восстановление непрерывной функции по отсчётам.

Цель лекции:

- установить возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром, исходя из отсчетных значений (выборок), взятых через равные промежутки времени.

Способ получения моделей сигналов состоит в следующем. Реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Если теперь устремить к нулю длительность отдельных элементарных сигналов, то, естественно, в пределе будет получено точное представление исходного сигнала. Будем называть этот способ описания сигналов динамическим представлением, подчеркивая этим развивающийся во времени характер процесса.

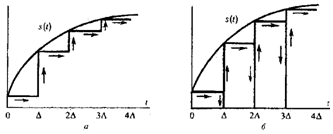
Широкое применение нашли два способа динамического представления. Согласно первому из них, в качестве элементарных сигналов используются ступенчатые функции, возникающие через равные промежутки времени (см. рисунок 4.1 а). Высота каждой ступеньки равна приращению сигнала на интервале времени .

При втором способе элементарными сигналами служат прямоугольные импульсы. Эти импульсы непосредственно примыкают друг к другу и образуют последовательность, вписанную в кривую или описанную вокруг нее (см. рисунок 4.1б).

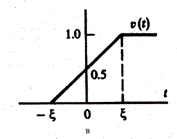
Рассмотрим свойства элементарного сигнала, используемого для динамического представления по первому способу.

Если функция описывает процесс перехода некоторого физического объекта из «нулевого» в «единичное» состояние. Математическая модель предельного сигнала получила название функции включения или функции Хевисайда.

0, t<0,

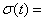½, t=0, (4.1)

1, t>0.

В теоретической радиотехнике функции включения широко используются для описания разрывных, в частности, импульсных сигналов.

s ( t ) = s ₀ ( t )+ (4.2)

Переходя ко второму способу динамического представления сигнала, когда элементами разложения служат короткие импульсы, следует ввести новое важное понятие.

Рассмотрим импульсный сигнал прямоугольной формы, заданный следующим образом

. (4.3)

При любом выборе параметра площадь этого импульса равна единице

Пусть теперь величина стремится к нулю. Импульс, сокращаясь по длительности, сохраняет свою площадь, поэтому его высота должна неограниченно возрастать. Предел последовательности таких функций при 0 носит название дельта-функции, или функции Дирака: (4.4)

Дельта-функция — интересный математический объект. Будучи равной нулю всюду, за исключением точки t = 0 (принято говорить, что она сосредоточена в этой точке), дельта-функция тем не менее обладает единичным интегралом:

. (4.5)

Вернемся к задаче описания аналогового сигнала суммой примыкающих друг к другу прямоугольных импульсов (см. рисунок 4.1,б).

. (4.6)

Итак, если непрерывную функцию умножить на дельта-функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен -импульс. Принято говорить, что в этом состоит фильтрующее свойство дельта-функции.

Для точного представления произвольной непрерывной функции 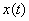на конечном интервале времени необходимо располагать данными о мгновенных значениях (отсчётах) этой функции во всех точках интервала, т.е. непрерывным множеством отсчётов, отстоящих друг от друга на бесконечно малые интервалы. Некоторое приближённое представление о функции 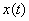можно составить по её отображению в виде дискретной последовательности импульсов, имеющих на интервалах значения , называемых отсчётами.

Рисунок 6.1.

Операция замены непрерывной функции последовательностью отсчётов её мгновенных значений называется дискретизацией. В качестве простейшей физической модели дискретизации рассмотрим коммутационное устройство (см. рисунок 4.2 а).

С помощью ключа Кл обеспечивается периодическое с частотой дискретизации подключение к источнику непрерывного сигнала 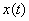(см. рисунок 4.2 б) на время , т.е. производится замена непрерывной функции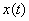последовательностью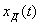на интервалах (см. рисунок 4.2 в).

Дискретный сигнал

В спектральной области произведению функций времени соответствует свёртка их спектров. Пусть спектр функции 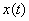финитен и имеет вид, представленный на рисунке 4.3 а, где - верхняя (граничная) частота. Спектр периодической последовательности импульсов дискретизации является линейчатым (см. рисунок 4.3 б); частота дискретизации определяется интервалом дискретизации . Спектры дискретизированного сигнала представлены для случаев, когда (см. рисунок 4.3 в), (см. рисунок 4.3 г) и (см. рисунок 4.3 д). Для неискажённого воспроизведения функции x ( t ) по последовательности отсчётов посредством идеального фильтра низких частот необходимо выбирать частоту дискретизации так, чтобы спектральные компоненты свёртки с каждой и дискретных составляющих периодической функции располагались в не перекрывающихся областях (см. рисунок 4.3). Этому соответствуют значения . При спектральные области перекрываются, в полосу частот дискретизируемого сигнала попадут спектральные компоненты смежных областей и возникнут искажения при восстановлении функции по отсчётам. Для точного воспроизведения непрерывной функции с ограниченным (финитным) спектром достаточно располагать значениями функции (отсчётами) лишь в отдельных точках. Модели сигналов с ограниченным спектром часто используются в технике связи.

Теорема отсчётов Котельникова: непрерывная функция 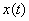, не содержащая частот выше граничной , полностью определяется отсчётами мгновенных значений в точках, отстоящих друг от друга на интервалы . Интервал называется интервалом Котельникова. Эта теорема позволяет представить непрерывную функцию 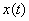в виде ряда

. (4.7)

Из сопоставления ряда (4.7) с общим видом обобщённого ряда Фурье в пространстве Гильберта следует, что элементарными базисными функциями в разложении Котельникова являются отсчетные функции.

. (4.8)

где постоянная вводится с учетом нормировки функций (4.8).

Процедура восстановления непрерывной функции 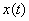по отсчётам её мгновенных значений вытекает непосредственно из (4.7): нужно перемножить значения отсчётов на соответствующие отсчётные функции (4.8) и просуммировать полученные произведения. Эти операции иллюстрирует рисунок 4.4. Спектральная трактовка процесса восстановления 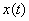следует из рисунка 4.3. Для полного восстановления необходимо просуммировать бесконечное множество членов ряда (4.7). Однако если функция с ограниченным спектром 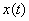рассматривается на конечном интервале Т (см. рисунок 4.4, а), то точное разложение (6.1) можно заменить следующим приближённым разложением

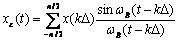. (4.9)

Конечное число отсчётов п, определяющее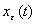, равно (), . Параметр , играющий важную роль в ТЭС, называют базой сигнала.

Дата добавления: 2018-09-20; просмотров: 623; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!