Лекция 12. Спектральный анализ непериодических сигналов. Преобразование Фурье. Спектральные плотности неинтегрируемых сигналов. Энергетические спектры сигналов
Содержание лекции:
- периодическое продолжение импульса. Понятие спектральной плотности сигнала.Обратное преобразование Фурье. Условие существования спектральной плотности сигнала.Связь между длительностью импульса и шириной его спектра.Обобщенная формула Рэлея.Взаимная спектральная плотность сигналов. Энергетический спектр.Корреляционный анализ сигналов.Сравнение сигналов, сдвинутых во времени.
Цель лекции:
- получить спектральные характеристики непериодических (импульсных) сигналов методом обобщения рядов Фурье. Определить требования к ширине полосы пропускания радиотехнического устройства. Представить сигналы посредством их спектральных плотностей. Использовать энергетический спектр для получения различных инженерных оценок. Понять, как возникает потребность в сигналах со специально выбранными свойствами.
Пусть s (t) - одиночный импульсный сигнал конечной длительности. Дополнив его мысленно такими же сигналами, периодически следующими через некоторый интервал времени T, получим изученную ранее периодическую последовательность Sпер ( t ), которая может быть представлена в виде комплексного ряда Фурье
(12.1) с коэффициентами 
. (12.2)
Для того, чтобы вернуться к одиночному импульсному сигналу, устремим к бесконечности период повторения Т. При этом очевидно:
а) частоты соседних гармоник nω1 и (n+ l)ω1 окажутся сколь угодно близкими, так что в формулах (12.1) и (12.2) дискретную переменную nω1можно заменить непрерывной переменной ω — текущей частотой;
|
|
|
б) амплитудные коэффициенты Сnстанут неограниченными малыми из-за наличия величины Т в знаменателе формулы (12.2).
Наша задача состоит теперь в нахождении предельного вида формулы (12.1) при T→∞.
Рассмотрим малый интервал частот Δω, образующий окрестность некоторого выбранного значения частоты ω0. В пределах этого интервала будет содержаться N=Δω/ω1= ΔωT/(2π) отдельных пар спектральных составляющих, частоты которых отличаются сколь угодно мало. Поэтому составляющие можно складывать так, как будто все они имеют одну и ту же частоту и характеризуются одинаковыми комплексными амплитудами 
В результате находим комплексную амплитуду эквивалентного гармонического сигнала, отображающего вклад всех спектральных составляющих, содержащихся внутри интервала Δω
. (12.3)
Функция 
(12.4)
носит название спектральной плотностисигнала s (t). Формула (12.4) осуществляет преобразование Фурье данного сигнала.
Решим обратную задачу спектральной теории сигналов: найдем сигнал по его спектральной плотности, которую будем считать заданной.
|
|
|
.
Поскольку в пределе частотные интервалы между соседними гармониками неограниченно сокращаются, последнюю сумму следует заменить интегралом
. (12.5)
Эта важная формула называется обратным преобразованием Фурье для сигнала s(t).
Сформулируем окончательно фундаментальный результат: сигнал s ( t ) и его спектральная плотность S(ω) взаимно однозначно связаны прямым и обратным преобразованиями Фурье
, (12.6)
.
Спектральное представление сигналов открывает прямой путь к анализу прохождения сигналов через широкий класс радиотехнических цепей, устройств и систем.
Сигналу s(t) можно сопоставить его спектральную плотность s(ω) в том случае, если этот сигнал абсолютно интегрируем, т. е. существует интеграл
.
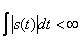Подобное условие значительно сужает класс допустимых сигналов. Так, в указанном классическом смысле невозможно говорить о спектральной плотности гармонического сигнала и (t) =Umcosω0t ,существующего на всей бесконечной оси времени.
Важный вывод: чем меньше длительность импульса, тем шире его спектр.
Под шириной спектра понимают частотный интервал, в пределах которого модуль спектральной плотности не меньше некоторого наперед заданного уровня, например, изменяется в пределах от |S|max, до 0.1|S|max.
|
|
|
Произведение ширины спектра импульса на его длительность есть постоянное число, зависящее только от формы импульса и, как правило, имеющее порядок единицы: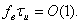 
Чем короче длительность импульса, тем шире должна быть полоса пропускания соответствующего усилителя. Короткие импульсные помехи имеют широкий спектр и поэтому могут ухудшать условия радиоприема в значительной полосе частот.
Математические модели многих сигналов, широко применяемых в радиотехнике, не удовлетворяют условию абсолютной интегрируемости, поэтому метод преобразований Фурье в обычном виде к ним неприменим. Однако можно говорить о спектральных плотностях таких сигналов, если допустить, что эти плотности описываются обобщенными функциями.
Пусть два сигнала и( t ) и v ( t ),в общем случае комплексно-значные, определены своими обратными преобразованиями Фурье.
Найдем скалярное произведение этих сигналов, выразив один из них, например v ( t ),через его спектральную плотность
Полученное соотношение представляет собой обобщенную формулу Рэлея. Легко запоминающаяся трактовка этой формулы такова: скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей. Если сигналы тождественно совпадают, то скалярное произведение становится равным энергии
|
|
|
. (12.7)
Назовем взаимным энергетическим спектромвещественных сигналов u(t) и v(t) функцию
, (12.8)
такую, что
. (4.9)
Нетрудно заметить, что Re Wuv(ω)—четная, а Im Wuv(ω)—нечетная функция частоты. Вклад в интеграл (12.9) дает только вещественная часть, поэтому
. (12.10)
Последняя формула дает возможность проанализировать «тонкую структуру» взаимосвязи сигналов.
Более того, обобщенная формула Рэлея, представленная в виде (12.10), указывает на принципиальный путь, позволяющий уменьшить степень связи между двумя сигналами, добившись в пределе их ортогональности. Для этого один из сигналов необходимо подвергнуть обработке в особой физической системе, называемой частотным фильтром. К этому фильтру предъявляется требование: не пропускать на выход спектральные составляющие, находящиеся в пределах частотного интервала, где вещественная часть взаимного энергетического спектра велика. Частотная зависимость коэффициента передачи такого ортогонализирующего фильтра будет обладать резко выраженным минимумом в пределах указанной области частот.
Спектральное представление энергии сигнала легко получить из обобщенной формулы Рэлея, если в ней сигналы и(t) и v ( t )считать одинаковыми. Формула (12.8), выражающая спектральную плотность энергии, приобретает вид
. (12.11)
Величина Wu(ω) носит название спектральной плотности энергии сигнала и(t), или, короче, его энергетического спектра. Формула (3.2) при этом запишется так
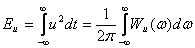. (12.12)
Соотношение (4.12) известно как формула Рэлея(в узком смысле), которая констатирует следующее: энергия любого сигнала есть результат суммирования вкладов от различных интервалов частотной оси.
Изучая сигнал с помощью его энергетического спектра, мы неизбежно теряем информацию, которая заключена в фазовом спектре сигнала, поскольку в соответствии с формулой (4.11) энергетический спектр есть квадрат модуля спектральной плотности и не зависит от ее фазы.
Обратимся к упрощенной идее работы импульсного радиолокатора, предназначенного для измерения дальности до цели. Здесь информация об объекте измерения заложена в величине τ — задержке по времени между зондирующим и принятым сигналами. Формы зондирующего и(t) и принятого и(t-τ) сигналов одинаковы при любых задержках. Структурная схема устройства обработки радиолокационных сигналов, предназначенного для измерения дальности, может выглядеть так, как это изображено на рисунке 12.1.
Рисунок 12.1 - Устройство для измерения времени задержки сигналов
Дата добавления: 2018-09-20; просмотров: 759; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!