Лекция 16. Модель дискретно-непрерывного канала. Критерии качества и правила приема дискретных сообщений. Теория помехоустойчивости систем передачи дискретных сообщений
Содержание лекции:
- модель дискретно-непрерывного канала.Критерий Котельникова. Оптимальные алгоритмы приема при полностью известных сигналах (когерентный прием).
Цель лекции:
- дать математическое описание канала. Синтезировать оптимальный демодулятор.
Дискретно-непрерывный канал с независимыми символами bi, на входе и непрерывным сигналом z ( t ) на выходе описывается априорными вероятностями входных символов P ( bi ) и переходными (условными) плотностями w[z|bi] принимаемой реализации z { t )(на заданном интервале Т) при условии передачи символа bi . Эту плотность называют функцией правдоподобия. Вместо функций правдоподобия дискретно-непрерывный канал можно описать апостериорными вероятностями Р( bi | z ) передачи символа bi; при фиксации на приёме колебанияz ( t ). Согласно формуле Байеса 
,
где плотность принимаемого колебания 
, (16.1)
где P ( bi ) — априорная вероятность передачи символа bi (т.е. та вероятность, которая имеет место до наблюдения и анализа, и определяемая статистикой источника сообщения и правилом кодирования).
Рассмотрим сначала широко распространённыйкритерий Котельникова или критерий идеального наблюдателя, согласно которому качество демодулятора оценивают безусловной (средней) вероятностью правильного приёма символа.
Пусть на вход демодулятора в течение отрезка [0, T] приходит некоторый элемент сигнала z ( t ).Предположим, что демодулятор принимает при этом решение, что передан символ bi, т.е. выдаёт оценку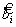 
. Вероятность того, что это решение правильно, очевидно, равна условной вероятности P(bi | z ( t )) того, что действительно передавался символ bi, при условии прихода реализации элемента сигнала z ( t ). Её называютапостериорной вероятностью символа bi (т.е. вероятностью, определённой после опыта, заключающегося в наблюдении и анализе сигнала z ( t )).
|
|
|
Другими словами, критерий идеального наблюдателя обеспечивается решающей схемой, построенной по правилу максимума апостериорной вероятности — решение 
, принимается в том случае, если выполняется система из т -неравенств
. (16.2)
Для двоичной системы сигналов упомянутое правило сводится к проверке неравенства
P (1| z ) > P (0| z ). (16.3)
При выполнении неравенства (16.3) регистрируется символ 1, в противном случае — 0.
Подставив (16.1) в (16.2) и учитывая, что w(z) — безусловная плотность вероятности, не являющаяся функцией i, можно записать правило решения по критерию идеального наблюдателя в следующей форме
Приёмник, реализующий этот алгоритм , называют приёмником Котельникова. Для двоичной системы правило сводится к проверке неравенства
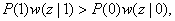(16.4)
при выполнении которого регистрируется символ 1, а при невыполнении — 0.
|
|
|
Для построения решающей схемы по правилу критерия идеального наблюдателя необходимо знать априорные вероятности символов P ( bi ), а также свойства модулятора и канала, определяющие условные плотности w(z|bi),j - функции правдоподобия.
Критерий Котельникова можно записать иначе. Решение о том, что передавался символ bi должно приниматься, если для всех j ≠ iвыполняются т —1 неравенств 
. (16.5)
Отношение в левой части этого неравенства называется отношением правдоподобиядвух гипотез: о том, что передавался символ bi , и о том, что передавался символ bj . Его обозначают Λij,.
В случае, когда все тсимволов передаются равновероятно, т.е. P ( bi ) = 1/m, правило (16.5) упрощается
Λ ij >1, i 
. (16.6)
Иногда вводят в рассмотрение помимо т гипотез о передаче символов 
ещё дополнительную ("шумовую") гипотезу о том, что никакой сигнал не передавался, т.е. z ( t ) == n ( t ) — чистая помеха. Отношение правдоподобия 
обычно обозначают просто Λi. Тогда правило (16.6) можно записать так
Λi > Λjпри всех j ≠ i. (16.7)
Такое правило максимума правдоподобия реализует критерий идеального наблюдателя при том условии, что все символы передаются равновероятно.
|
|
|
Для двоичной системы правило (16.7) сводится к проверке неравенства
Λ1>Λ0. (16.8)
В технике связи преимущественно применяют правило максимального правдоподобия (16.7), (16.8). В том случае, когда все символы передаются равновероятно, правило максимального правдоподобия реализует критерий идеального наблюдателя. Однако очень часто это правило решения применяют и при неизвестных или известных, но не одинаковых априорных вероятностях символов. Конечно, оно не обеспечивает в этих случаях максимума вероятности правильного приёма. Изменив решающую схему на схему, построенную по правилу максимальной апостериорной вероятности (16.3), реализующему критерий идеального наблюдателя, можно было бы уменьшить вероятность ошибок. При этом, очевидно, пришлось бы сократить области приёма маловероятных и расширить области высоковероятных символов. В результате редко передаваемые символы принимались бы менее надёжно, нежели часто передаваемые. Но редкие символы несут больше информации, чем частые. Поэтому переход от правила максимального правдоподобия к правилу максимальной апостериорной вероятности, хотя и уменьшает безусловную вероятность ошибки, может привести к увеличению потери информации при демодуляции.
|
|
|
Предположим, что все искажения в канале строго детерминированы и случайным является только гауссовский аддитивный шумn ( t ), который вначале полагаем белым, со спектральной плотностью N 0 .Это значит, что при передаче символа bi (i=0,1,…,m-1) принимаемое колебание можно описать моделью:
z(t)=si(t)+n(t), 0 ≤ t ≤T, (16.9)
где все si ( t )= γf ( t - τ - kT , bk ( i ) ) = γui(t-τ) известны.
Определим в этих условиях алгоритм работы оптимального (т.е. основанного на правиле максимального правдоподобия) демодулятора, анализирующего сигнал на тактовом интервале О...T. Для этого необходимо найти отношения правдоподобия для всех твозможных сигналов относительно нулевой гипотезы ( z ( t )= n ( t )). Задача затрудняется тем, что ширина спектра сигнала бесконечна (поскольку он финитный), а поэтому пространство сигналов бесконечномерное L 2 ( T ). Для таких сигналов (или бесконечномерных векторов) не существуют плотности вероятностей. Однако существуют n-мерные плотности вероятностей для любых п сечений сигнала.
Заменим вначале белый шум квазибелым, имеющим ту же одностороннюю спектральную плотность мощности N 0 , но только в некоторой полосе частот F = п/2Т,где n>>1. Рассмотрим дополнительную гипотезу, т.е. будем считать, что z ( t ) -стационарный шум с нулевым МО. Возьмём на тактовом интервале п равноотстоящих сечений через Δt=1/2F=T/n.Отсчёты Z 1 ,..., Zn в этих сечениях для квазибелого гауссовского шума независимы. При гипотезе, что передавался символ bi, согласно (16.9) n ( t )= z ( t )- si ( t ).
Вернёмся к исходной задаче для белого шума. Для этого будем расширять полосу F, тогда число сечений пстремится к бесконечности, а Δt — к нулю. Правило приёма сводится к проверке системы неравенств
, (16.10)
где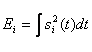 
—энергия ожидаемого сигнала Si ( t ).Выражение (16.10) определяет те операции (алгоритм приёма), которые должен совершать оптимальный приёмник над входным колебанием. Для двоичной системы алгоритм (16.10) сводится к проверке одного неравенства
(16.11)
При выполнении неравенства (16.11) регистрируется символ "1", в противном случае "0".
Устройство, непосредственно вычисляющее скалярное произведение (или корреляционный интеграл) 
, (16.12)
называют активным фильтром или коррелятором,поэтому приёмник, реализующий алгоритм (16.10), называют корреляционным.
На рисунке 16.1 показана структурная схема приёмного устройства, работающего в
| |
соответствии с (16.11).
Если сигналы ui ( t )выбраны таким образом, что все их реализации (а следовательно, и все реализации si ( t )) имеют одинаковые энергии (Ei =const), алгоритм приёма (16.10) (и соответственно его реализация) упрощается (отпадает необходимость в вычитающих устройствах) и принимает вид
. (16.13)
Из (16.13) видно, что правило решения не изменится, если сигнал z ( t ),поступающий на вход демодулятора, умножить на любое число. Поэтому система, в которой все реализации сигнала имеют равную энергию, отличается тем, что оптимальный алгоритм приёма в ней не требует знания "масштаба" приходящего сигнала или, другими словами, знания коэффициента передачи γ канала. Эта особенность обусловила широкое распространение систем сигналов с равной энергией, что важно для каналов с замираниями, в которых коэффициент передачи флуктуирует. Заметим, что для двоичной системы неравенство (13.11) можно представить в более простом виде
, (16.14)
где sΔ(t)=s1(t)-s0(t) —разностный сигнал;
λ = 0,5(E1-E0) — пороговый уровень.
Дата добавления: 2018-09-20; просмотров: 405; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!