Лекция 18. Помехоустойчивость оптимального когерентного приема. Теоремы Шеннона

Содержание лекции:

- помехоустойчивость оптимального когерентного приема. Теоремы Шеннона.

Цель лекции:

- определить потенциальную помехоустойчивость для двоичной системы с аддитивным БГШ в канале, когда при приёме точно известны оба ожидаемых сигнала: s ₁ ( t ) иs ₀ ( t ), полагая, что априорные вероятности этих сигналов одинаковы.

Приходящий сигнал z ( t )является случайным, так как, во-первых, заранее не известна реализация передаваемого сигнала, во-вторых, он содержит случайную помеху N ( t )

В этом случае согласно (5.26) алгоритм оптимального приёма

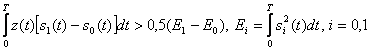. (18.1)

При выполнении неравенства (18.1) оптимальный приёмник регистрирует символ 1, соответствующий сигналу s ₁ ( t ), в противном случае — символ 0, соответствующий сигналу S ₀ ( t ).Если действительно передаётся символ 1, то z ( t ) = s ₁ ( t ) + N ( t ). При этом вероятность ошибки определяется вероятностью того, что неравенство (18.1) не выполнено, т.е. вероятностью выполнения обратного неравенства.

Если N ( t ) -нормальный белый стационарный шум с нулевым средним и односторонней спектральной плотностью мощности N ₀ , то вероятность ошибки через Q-функцию можно записать в виде

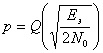. (18.2)

Функция табулирована и называется дополнительной функцией ошибок. При заданной интенсивности помехи NQпотенциальная помехоустойчивость двоичной системы зависит только от так называемой эквивалентной энергии сигналов

, (18.3)

которая равна квадрату расстояния между сигнальными точками в пространстве Гильберта. Помехоустойчивость выше (вероятность ошибки меньше) у той системы, у которой больше эквивалентная энергия используемых сигналов независимо от формы используемых сигналов. Последние, в частности, могут быть как простыми (отрезками синусоиды с малой базой), так и сложными (шумоподобными, с большой базой).

На рисунке 18.1 в двумерном пространстве показаны точки сигналов для двоичной системы: рисунок 18.1 а - AM при s ₀ ( t )=0,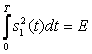;рисунок 18.1 б —ЧМ с ортогональными сигналами , ; рисунок 18.1 в — ФМ с противоположными сигналами s ₁ ( t )=- s ₀ ( t ).

Из рисунка видно, что по сравнению с двоичной AM для двоичной ЧМ

Рисунок 18.1 - К определению эквивалентной энергии двоичных систем AM, ЧМ, ФМ

эквивалентная энергия сигнала E_э=||s₁- s₀||² в 2 раза больше, а для двоичной ФМ - в 4 раза больше.

Соотношение (18.3) позволяет осуществлять оптимальный выбор сигналов s ₁ ( t ) и S ₀ ( t ) или соответственноu ₁ ( t ) и У₀(t), обеспечивающих максимально возможную помехоустойчивость при заданной энергии сигналов Е.

Интеграл принимает только неотрицательные значения, поэтому его минимум равен нулю и достигается при условии s ₁ ( t )=- s ₀ ( t ), в двоичном канале с постоянными параметрами и аддитивным БГШ оптимальной оказывается система с противоположными сигналами. Этому условию удовлетворяют, например, двуполярные импульсы, сигналы двоичной фазовой модуляции (ФМ), если разность фаз сигналов Δφ=π и.т.п.

Для всех таких систем Е_э = 4Е и вероятность ошибки

, (18.4)

где отношение энергии сигнала на входе демодулятора к спектральной плотности мощности флуктуационной помехи.

Для системы с ортогональными сигналами равной энергии (например, при известных условиях для системы двоичной ЧМ), когда 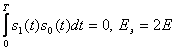и минимальная вероятность ошибки

p = Q ( h ). (18.5)

Сравнивая (18.5) и (18.4), приходим к выводу, что переход от системы с ортогональными сигналами к системе с оптимальными (противоположными) сигналами позволяет в рассматриваемом канале обеспечить неизменное качество связи (вероятность ошибки) при понижении средней мощности передатчика в 2 раза, т.е. даёт энергетический выигрыш в 2 раза (или на 3 дБ). Этот вывод следует также из рисунка 18.1.

В двоичной системе с пассивной паузой, полагая s ₀ ( t )=0 и 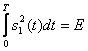, получаем для минимальной вероятности ошибки

. (18.6)

Отсюда видно, что при переходе от системы AM к системе ЧМ энергетический выигрыш по максимальной мощности равен 2, а при переходе к системе ФМ - 4. Если же сравнение вести не по пиковой, а по средней мощности, то переход от AM к ЧМ не даёт энергетического выигрыша, поскольку при ЧМ средняя мощность равна максимальной, а при AM - вдвое меньше максимальной (если s₁ и s₀передаются с одинаковой вероятностью).

Система ФМ, как и другие системы с противоположными сигналами, обеспечивает максимальную для двоичной системы потенциальную помехоустойчивость. Однако реализация демодулятора для когерентного приёма ФМ встречает определённые трудности. При построении демодулятора с активным фильтром возникает проблема поддержания равенства фаз опорного генератора и приходящего сигнала. Если пытаться строить его на основе согласованного фильтра (см. рисунок 17.2), то возникает не менее трудная задача взятия когерентного отсчёта. Возникает так называемое явление обратной работы,вследствие которого практическое внедрение системы с двоичной фазовой модуляцией оказалось затруднительным.

Эффективный метод устранения этого явления был найден путём перехода к относительным методам модуляции,предложенным Н.Т. Петровичем. Они сводятся к модуляции информационного параметра передаваемой посылки элемента сигнала относительно того же параметра предшествующей посылки. При относительной фазовой манипуляции(ОФМ) сообщение содержится не в абсолютном значении фазы элемента сигнала, а в разности фаз двух соседних элементов, при этом символ 1 передаётся повторением той реализации сигнала, которая имела место в качестве предыдущего элемента, а символ 0 — реализацией с обратной фазой, либо наоборот.

Сигналы ОФМ могут приниматься различными методами. Рассмотрим квазикогерентный приём сигналов ОФМ (называемый методом сравнения полярностей).

Определим вероятность ошибки в системе ОФМ при учёте флуктуационной помехи в канале при когерентном приёме. Очевидно, что ошибочная регистрация символа при приёме методом сравнения полярностей возможна в результате одного из двух несовместных событий:

а) знак данного элемента принят ошибочно, а знак предыдущего - верно;

б) знак данного элемента принят верно, а знак предыдущего - ошибочно.

Каждое из этих событий имеет вероятность p _ФМ(1-p _ФМ)- Таким образом, в нормальных условиях эксплуатации, когда требуется p _ФМ<<1,p _ОФМ =2 p _ФМ =2 Q [ ].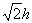

Таким образом, "платой" за устранение обратной работы является удвоение вероятности ошибки, обусловленной шумом в канале.

Очевидно, что при рассматриваемом методе приёма сигналов ОФМ образующийся дискретный канал является марковским. Вероятность ошибки в нём зависит от того, правильно или ошибочно приняты предыдущие символы. Подавляющее большинство ошибок группируется по две.

Для систем равновероятных ортогональных сигналов равной энергии канал симметричен, и можно оценить вероятность ошибки простым неравенством

. (18.7)

Теорема 1. О кодировании источника.

Существует способ кодирования, при котором средняя длина последовательности канальных символов п , приходящаяся на один символ источника сообщений,

. (18.8)

Не существует способа кодирования, при котором меньше, чем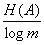

Теорема 2. Основная теорема Шеннона.

Если производительность источника H ¢ ( A ) меньше пропускной способности С ¢ в единицу времени дискретного канала с помехами, то при любом d > 0 существует способ кодирования и декодирования источника и канала, при котором сообщения передаются получателю с вероятностью ошибки меньшей, чем d , и в среднем без растущих задержек во времени. Если H ¢ ( A ) > С ¢ , то такого способа кодирования не существует.

Не всегда следует использовать как канальное кодирование, так и кодирование источника. Последнее для достижения заметного эффекта может оказаться нереализуемо сложным.

Дата добавления: 2018-09-20; просмотров: 997; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 10 11 12 13 14 15 161718 19 Следующая ⇒

Мы поможем в написании ваших работ!