Дифференциальные уравнения в полных дифференциалах

1º. Основные понятия

Рассмотрим ОДУ в дифференциальной форме

M(x, y)dx + N(x, y)dy = 0, (1)

Считаем, что функции M(x, y), N(x, y) — непрерывные по обеим переменным в некоторой односвязной области D плоскости XOY, причём

M²(x, y) + N²(x, y) ¹ 0.

Определение 1. ОДУ (1) называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции двух переменных.

Таким образом, если (1) — уравнение в полных дифференциалах, то существует функция u(x, y), такая что

du(x, y) = M(x, y)dx + N(x, y)dy.

Тогда ОДУ (1) можно записать в виде

du(x, y) = 0.

Автоматически следует, что общий интеграл этого уравнения

u(x, y) = C.

Пример 1. ydx + xdy = 0.

Левая часть уравнения есть полный дифференциал функции u(x, y) = xy.

Действительно,

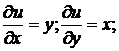
поэтому полный дифференциал имеет вид d(xy) = ydx + xdy Þ d(xy) = 0

И общий интеграл этого уравнения xy = C.

На практике, чтобы использовать этот метод интегрирования, нужно решить две задачи:

1). Каким образом можно отличить дифференциальное уравнение в полных дифференциалах от остальных.

2). Как найти функцию двух переменных, если известен её полный дифференциал.

Этим мы и будем заниматься.

2º. Признак уравнения в полных дифференциалах

Теорема 1. Пусть функции M(x, y), N(x, y) — непрерывно дифференцируемые в отмеченной области D. Уравнение (1) будет уравнением в полных дифференциалах, тогда и только тогда, когда для функций M(x, y), N(x, y) выполняется условие Эйлера

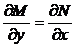" (x, y) Î D. (2)

Доказательство. Необходимость. Считаем, что существует функция u(x, y), что

du(x, y) = M(x, y)dx + N(x, y)dy.

С другой стороны

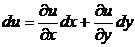поэтому имеем тождество

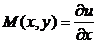, (3)

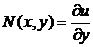. (4)

Дифференцируем (3) по y, (4) по x:

, .

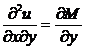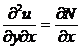Так как частные производные функций M(x, y), N(x, y) непрерывные по условию, поэтому будут непрерывными смешанные производные функции u(x, y). А это значит, они равны между собой, тогда выполняется условие Эйлера

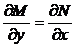Достаточность. Считаем, что выполняется условие Эйлера (2). Нужно показать, что существует функция u(x, y), для которой выполняются равенства (3), (4).

Доказательство конструктивное— функция u(x, y) строится.

Сначала рассмотрим формулу (3) как уравнение относительно неизвестной функции u(x, y)

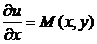. (3¢)

Фиксируем точку (x₀, y₀) Î D, которая принадлежит D вместе с некоторой окрестностью.

В этой же окрестности рассмотрим подвижную точку (x, y).

Из (3¢) найдём выражение для функции u(x, y) интегрированием по x на прамежутке от x₀ до x:

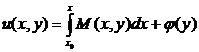. (5)

Интеграл имеет смысл, т.к. M(x, y) – непрерывная. Здесь j(y) — любая функция, дифференцируемая по y, т.к. производная 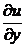должна существовать.

Найдём выражение для производной по y

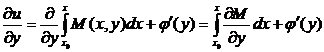Поднесение знака дифференцирования под знак интеграла возможно, т.к. функция M(x, y) и её производная 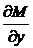непрерывные по обеим переменным.

С другой стороны, из равенства (4) имеем

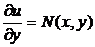, (4¢)

поэтому

N(x, y) = .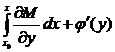

Воспользовавшись формулой Эйлера (2)

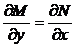делаем замену функции под интегралом

N(x, y) = 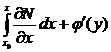. (6)

Интегрируем

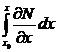= N(x, y) – N(x₀, y).

Из (6) получаем

N(x, y) = N(x, y) – N(x₀, y) + j¢(y).

Тогда j¢(y) = N(x₀, y) и

j(y) = 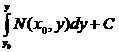, (7)

где C — произвольная константа.

Из (5) и (7) получаем формулу для функции u(x, y)

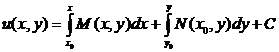Нам нужна одна функция, а мы получили семейство функций. Считаем C = 0 и

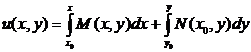Теорема доказательствоана.

Замечание. Достаточность условия Эйлера в теореме можно доказательствоать, используя криволинейный интеграл. При таком подходе функция u(x, y) определяется криволинейным интегралом от дифференциальной формы

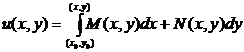
Так как дифференциальная форма является полным дифференциалом, то значение интеграла не зависит от пути интегрирования, а только от начальной и конечнойточек.

3º. Метод нахождения общего интеграла

Метод интегрирования уравнения в полных дифференциалах фактически определяется доказательствоательством достаточности в теореме. Формула общего интеграла имеет вид

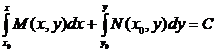
нужно отметить, что доказательство достаточности можно было бы начать с интегрирования формулы

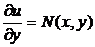, (4¢)

тогда бы получили формулу

.

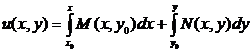Соответственно общий интеграл

.

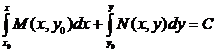Формулы равнозначные.

Пример 2. (y³ – 2xy) dx+ (3xy² – x²) dy= 0.

Это не уравнение с разделяющимися переменными.

Проверяемем условие Эйлера

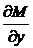= 3y² – 2x, 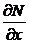= 3y² – 2x.

Выполняется. Воспользуемся первой формулой

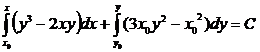В качестве точки (x₀, y₀) возьмём начало координат (0, 0)

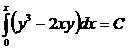Получаем общий интеграл

y³x – x²y = C.

4º. Интегрирующий множитель

Часто уравнение в дифференциальной форме

M(x, y)dx + N(x, y)dy = 0, (1)

уравнением в полных дифференциалах не является, но его можно свести к уравнению в полных дифференциалах с помощью умножения на некоторую функцию.

Определение 2. Интегрирующий множитель — это функция m(x, y), которая уравнение

M(x, y)dx + N(x, y)dy = 0

приводит к уравнению в полных дифференциалах

m(x, y)M(x, y)dx + m(x, y)N(x, y)dy = 0. (8)

Поскольку (8) — уравнение в полных дифференциалах, то должно выполняться условие Эйлера. Тогда

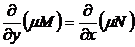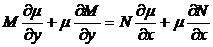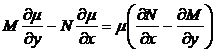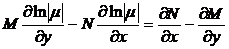Последнее уравнение — уравнение в частных производных, и, вообще говоря, более сложное, чем исходное. Но есть частные случаи.

Пример 3. Проверить, что для уравнения

(3x + 2y + y²)dx + (x + 4xy + 5y²)dy = 0

интегрирующий множитель имеет вид m(x, y) = x + y².

(x + y²)(3x + 2y + y²) = 2y(3x + 2y + y²) + (x + y²)(2 + 2y) = 2x + 8xy + 6y² +4y³

(x + y²)(x + 4xy + 5y²) = (x + 4xy + 5y²) + (x + y²)(1 + 4y) = 2x + 8xy + 6y² + 4y³

Формула Эйлера выполняется.

Одним из частных случаев существованя интегрирующего множителя является уравнение с разделяющимися переменными (§ 6)

M₁(x)N₁(y)dx + M₂(x)N₂(y)dy = 0. (9)

Делением на N₁(y)M₂(x) (умножением на 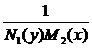) мы приводили его к уравнению с разделёнными переменными

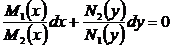Если проверить формулу Эйлера:

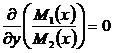и ,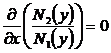

то получается, что уравнение с разделёнными переменными, есть уравнение в полных дифференциалах, а для уравнения (9) интегрирующий множитель имеет вид

m(x, y) = .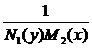

Дата добавления: 2018-08-06; просмотров: 526; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!