Дифференциальные уравнения с разделяющимися переменными
1º. Уравнения с разделёнными переменными
Рассмотрим ОДУ, записанное в дифференциальной форме
M(x, y)dx + N(x, y)dy = 0,
когда функции M(x, y) и N(x, y) имеют специальный вид:
M(x, y) = M(x), N(x, y) = N(y).
Определение 1. Уравнение вида
M(x)dx + N(y)dy = 0, (1)
где M(x) и N(y) – непрерывные функции называется дифференциальным уравнением с разделенными переменными.
Замечание 1. Разделённость переменных заключается в том, что возле dx находится функция зависящая только от x, а возле dy — функция зависящая только от y.
Такие уравнения легко разрешимы. Так как неизвестная функция y зависит от x, то нужно сначала разделить уравнение на dx и взять неопределённый интеграл по x:
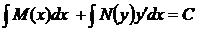 , или
, или 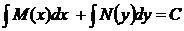 ,
,
где C — произвольная константа.
Таким образом, каждое слагаемое левой части можно интегрировать по своей переменной.
Пример 1. ex dx– y dy= 0.
Это уравнение с разделёнными переменными. Проинтегрируем обе части уравнения, получим
 , или ex –
, или ex – 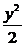 = C.
= C.
2º. Уравнение с разделяющимися переменными
Определение 2. Уравнение вида
M1(x)N1(y)dx + M2(x)N2(y)dy = 0 (2)
с непрерывными функциями M1(x), M2(x), N1(y), N2(y) называется дифференциальным уравнением с разделяющимися переменными.
Уравнение (2) сводится куравнению вида (1). Для этого выделяем те функции, которые мешают интегрированию — это N1(y) окло dx и M2(x) около dy. Разделим обе части уравнения на произведение N1(y) M2(x):
|
|
|
M1(x)N1(y)dx + M2(x)N2(y)dy = 0 | 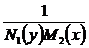 .
.
Врезультате получим уравнение с разделёнными переменными
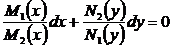
Далее его нужно проинтегрировать, как в п. 1º.
Замечание 2. При преобразовании уравнения (2) мы дзелили на произведение N1(y)M2(x). Но это возможно, если N1(y)M2(x) ¹ 0.
Но, если функциянальные уравнения
N1(y) = 0, M2(x) = 0
имеют числовые решения, например,
N1(y0) = 0, M2(x0) = 0,
то постоянные функции y = y0 и x0 = x0 также являются решениями уравнения (2). Чтобы эти решения не потерять нужно:
1) найти числовые решения уравнений N1(y) = 0, M2(x) = 0;
2) если их можно получить из общего решения при некоторойм значении постоянной С, то они входят в общее решение ДУ. В противном случае эти решения являются особыми решениями, их нужно добавить к общему решению уравнения (общему интегралу).
Пример 2. ydx – xdy = 0.
Разделим обе части уранения на произведение xy, при этом считаем, что x ¹ 0, y ¹ 0 (!).
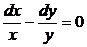
Интегрируем
ln|x| – ln|y| = C.
Воспользуемся свойствами логарифма и изменим форму произвольной константы C= ln|C1|, C1 ¹ 0, получим
ln|x/y| = ln|C1|, C1 ¹ 0,
потенцируем и получаем общий интеграл
x/y = C1, C1 ¹ 0.
Вернёмся к числовым уравнениям (!). Они имеют решения:x = 0 и y = 0, причём можно убедиться, что эти функции являются решениями дифференциального уравнения. Проверим, входят ли они в общий интеграл.
|
|
|
Функция x = 0 не входит в общий интеграл. Расширяем множество значений произвольной константы C1 Î(–µ, +µ) и добавляем функцию x = 0 в формулу общего интеграла.
Функция y = 0 не входит в общий интеграл. Её нужно дописать.
Вывод. Все решения описываются формулами
x/y = C, y = 0.
Пример 3. x(2 + y2)dx – y(2 + x2)dy = 0.
Делим уравнение на произведение (2 + y2)(2 + x2).
Считаем, что (2 + y2)(2 + x2) ¹ 0 (!).
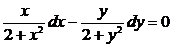 ,
,
 ,
,
 ,
,
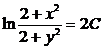 , 2C = ln|C1|, C1¹ 0,
, 2C = ln|C1|, C1¹ 0,
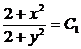 , C1 ¹ 0.
, C1 ¹ 0.
(!) Проверка показывает, что уравнения (2 + y2) = 0, (2 + x2) = 0 не имеют решений.
Замечание 3. Дифференциальное уравнение вида
y¢ = f1(x)f2(y) (3)
также называеся дифференциальным уравнением с разделяющимися переменными.
Можно показать, что это частный случай уравнения вида (2).
3º. Уравнения, которые приводятся к уравнениям вида (3)
К уравнениям вида (3) можно свести дифференциальные уравнения вида
y¢ = f(ax + by + c). (4)
Рассмотрим частные случаи
1). Случай b = 0. Уравнение имеет вид
y¢ = f(ax + c).
Это частный случай уравнения (3), оно разрешимо непосредственным интегрированием.
|
|
|
2) Случай a = 0. Уравнение имеет вид
y¢ = f(by + c).
Это частный случай уравнения (3) с разделяющимися переменными.
3). Случай ab ¹ 0. Делаем подстановку
u = ax + by + c,
где u — новая неизвестная функция от x.
Дифференцируем по x
u¢ = a + by¢
и находим выражение для производной y¢:
y¢ =  (u¢ – a).
(u¢ – a).
Подставляем в (4)
 (u¢ – a) = f(u), или u¢ = b (f(u) + a)
(u¢ – a) = f(u), или u¢ = b (f(u) + a)
Последнее уравнение есть частный случай уравнения (3) с разделяющимися переменными.
Пример 4.  .
.
Уравнение определено во всей плоскости XOY за исключением линии x = y.
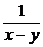 + 1 = f(x – y ) Þ a = 1, b = –1, c = 0 (третий случай).
+ 1 = f(x – y ) Þ a = 1, b = –1, c = 0 (третий случай).
Подстановка u = x – y, u¢ = 1 – y¢, y¢ = 1 – u¢.
Получаем уравнение
1 – u¢ = 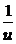 + 1, или
+ 1, или 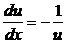 .
.
Пераводзим в дифференциальную форму и раздзяляем зменныя множаннем на u
udu + dx = 0.
Интегрируем
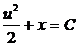 ,
,
возвращаемся к переменной y и получаем общий интеграл
 .
.
Дата добавления: 2018-08-06; просмотров: 341; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
