Линейные дифференцыяльные уравнения n–го порядка

Теорема. Если функции p₁(x), p₂(x), … , p_n(x), f(x) непрерывные на отрезке I = [a, b], тогда для любых начальных условий (2), где x₀ Î [a, b], существует единственное решение задачи Коши (1), (2).

Обозначим через

L(y) º y⁽ⁿ⁾ + p₁(x)y^{(n – 1)} + p₂(x)y^{(n – 2)} +… + p_{n – 1}(x)y¢ + p_n(x)y

левую часть ЛОДУ n–го порядка, тогда само ЛОДУ можно записать

L(y) = 0                                                          (1)

Замечаниею Оператор (функция) обладает свойством линейности, т.е.

L(C₁y₁ + C₂y₂) = C₁L(y₁) + C₂L(y₂)

Теорема 1. Если функции y₁, y₂, … , y_m являются решениями ЛОДУ (1), тогда линейная комбинация

C₁y₁ + C₂y₂ + ... + C_my_m,

где C₁, C₂, … , C_m Î R, также решение ЛОДУ (1).

Для описания пространства решений ЛОДУ (1) нам понадобится

Определение. Система (набор) функций u₁(x), u₂(x), … , u_m(x) называется линейна зависимой на отрезке [a, b], если для " x Î [a, b] одна из функций является линейной комбинацией остальных.

Линейная зависимость системы функций u₁(x), u₂(x), … , u_m(x) означает, что существуют такие числа a₁, a₂, ... , a_m, из которых хотя бы одно не равно нулю, такия, что на отрезке [a, b] выполняется равенство

a₁u₁(x) + a₂u₂(x) + … + a_mu_m(x) = 0.                                         (2)

Понятно, если одна из функций системы является нулевой ( º 0 на отрезке [a, b]), система функций будет линейно зависимой.

Определение. Если тождество (2) выполняется на отрезке [a, b] только в случае, когда все a_k , k = 1, 2, …, m, равны нулю, тогда система функций u₁(x), u₂(x), … , u_m(x) называется линейна независимой на отрезке [a, b].

Пример 1. Система функций 1, x, x², ... , x^m  линейно независимая на любом отрезке.

Действительно, соотношение вида (2) для данной системы функций имеет вид a₁ + a₂x + a₂x² +… + a_mx^m = 0.

На любом отрезке соотношение не может выполняться тождественно, если не все a_k , k = 1, 2, …, m, равны нулю, так как это многочлен степени невыше m, который может иметь не более m различных корней.

Теорема 2 (неабходимое условие линейной зависимости).Если функции u₁(x), u₂(x), … , u_m(x), определённые на отрезке [a, b], имеющие производные до порядка (m – 1) включительно, образуют линейно зависимую систему функций на отрезке [a, b], тогда на отрезке [a, b] тождественно равен нулю определитель

 º 0.

Без доказательства.

Определение. Определетель вида

W(x) º W[u₁, u₂, … , u_m] º

называется определителем Вронского или Вронскианом.

Вывод (достаточное условие линейной независимости). Если определетель Вронского системы функций u₁, u₂, … , u_m не ревен нулю хатя бы в одной точке отрезка [a, b], то система функций является линейно независимой.

Пример 2. Докажем снова, что на любом отрезке система функций

1, x, x², ... , x^m линейно независимая с помощью достаточного условия.

Покажем, что W[1, x, x², ... , x^m] ¹ 0.

W[1, x, x², ... , x^m] =  = 1×1×2!×3!×... ×m! ¹ 0, " x Î R.

Пример 3. Покажем, что функции  с разными действительными числами k₁, k₂, … , k_m образует линейно независимую на R систему функций.

Действительно,

W[ ] =  =

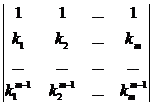= ×  ¹ 0, " x Î R.

Последний определитель называется определителем Вандермонда.

Определитель Вандермонда не равен нулю, если числа k₁, k₂, … , k_m не равны между собой.

Замечание. Равенство W(x) = 0 на отрезке не является достаточным условием для линейной зависимости системы функций.

Рассмотрим, например, систему функций

,    ,

для которой носители ненулевых значений не пересекаются.

На отрезке [0, 2] имеем равенство , так как на отрезке [0, 1] первый столбик W(x) равен нулю, а на отрезке [1, 2] — второй столбик.

Но система u₁(x), u₂(x) линейно зависимой не является, так как нет неравных нулю чисел a₁, a₂, таких, чтобы на отрезке [0, 2] выполнялосьтождество

a₁u₁(x) + a₂u₂(x) = 0.

Равенство нулю определителя Вронского на отрезке является достаточным условием для линейной зависимости системы n решений ЛОДУ n–го порядка.

Теорема 3 (критерий линейной независимости системы решений ЛОДУ).

Для того, чтобы система n решений y₁, y₂, ... , y_n ЛОДУ n–го порядка

L(y) = 0                                                          (1)

с непрерывными на [a, b] коэффициентами была линейно независимой на [a, b], необходимо и достаточно, чтобы

W[u₁, u₂, … , u_m] ¹ 0 " x Î [a, b].

Теорема 4. Если коэффициенты ЛОДУ n–го порядка

L(y) = 0,                                                         (1)

непрерывные на [a, b] функции, тогда существует линейно независимая на [a, b] система n решений ЛОДУ

Доказателбство. Фиксируем x₀ Î [a, b].

Сначала ЛОДУ (1) задаём начальные условия вида

y(x₀) = 1, y¢(x₀) = 0, ... , y^{(n – 1)}(x₀) = 0.                                       (6)

По теореме п. 2º § 12 существует единственное решение y₁(x) задачи Коши (1), (6).

Потом задаем другие начальные условия

y(x₀) = 0, y¢(x₀) = 1, ... , y^{(n – 1)}(x₀) = 0.                                       (7)

Пусть y₂(x) — единственное решение задачи Коши (1), (7).

Аналогично строим другие решения ЛОДУ (1).

y_n(x) — последние решение задачи Коши с начальными условиями

y(x₀) = 0, y¢(x₀) = 0, ... , y^{(n – 1)}(x₀) = 1.

Получили n решений ЛОДУ (1). Для этих решений

W(x₀) =  = 1 ¹ 0,

значит построенная система решений линейно независимая по выаоду из теоремы 2.

Теорема доказана.

Определение. Любая линейно независимая система n решений ЛОДУ (1) с непрерывными коэффициентами называется фундаментальной системой решений ЛОДУ (1).

Теорема 5. Общее решение ЛОДУ (1) с непрерывными коэффициентами имеет вид

y = C₁y₁ + C₂y₂ + ... + C_ny_n,                                  (8)

где y₁, y₂, ... , y_n — фундаментальная система решений ЛОДУ (1);

C₁, C₂, … , C_n — произвольные постоянные.

Доказательство. Проверим определение общего решения (§ 10).

Очевидно, что функция (8) меет непрерывные частные производные по x до порядка n включительно, и при любых C₁, C₂, … , C_n  функция (8) является решением линейного уравнения (1).

Покажем, что для любого набора x₀, y₀,  можно найти значения констант C₁, C₂, … , C_n.

Диффернцируем (8), подставляем набор значений и получаем систему

.

Определитель системы W(x₀) ¹ 0, поэтому существует нетривиальное решение C₁, C₂, … , C_n.

Вывод. Максимальное число линейно независимых решений ЛОДУ равно его порядку.

Свойства ЛНДУ n–го порядка

Теорема 1. (Структура общего решения ЛНДУ) Общее решение ЛНДУ

L(y) = f(x),                                                      (1)

с непрерывными коэффициентами есть сумма частного решения ЛНДУ (1) и общего решения соответствующего ЛОДУ.