Также рассматривают эквивалентные уравнения
| dy-f(x,y)dx=0, | (3) | |
| M(x,y)dx+N(x,y)dy=0. | (4) |
Заметим, что уравнение (4) получается из (3), если (3) умножить на некоторую функцию N(x,y)¹0. Будем считать, что коэффициенты M(x,y) и N(x,y) являются функциями, непрерывными в некоторой области. От уравнений (2) и (2') можно всегда перейти к (4) и наоборот.
Говорят, что если дифференциальные уравнения имеют вид (4), то они заданы в дифференциальной форме.
Рассматривают и уравнения в симметричной форме:
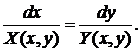
| (3') |
В случае, когда правая часть уравнения (2) не содержит у, то получаем дифференциальное уравнение вида:
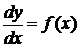 . .
| (5) |
Если функция f(x) определена и непрерывна на промежутке I, то любая первообразная функции f(x) на I является решением уравнения (5) и других решений нет.
Из мат. анализа известно, что при любом x0ÎI и произвольной постоянной С все первообразные содержатся в формуле
у(х)= 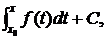 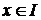
| (6) |
и поэтму решение уравнения (5) имеет вид (6).
Замечание. Если в качестве первообразной 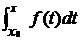 взять
взять 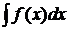 , то решение можно записать в виде
, то решение можно записать в виде
y(x)= 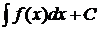 , ,
| (7) |
где под символом 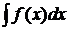 неабходимо понимать не множество всех перво-образных функций f(x), а одну какую-либо фиксированную первообразную этой функции.
неабходимо понимать не множество всех перво-образных функций f(x), а одну какую-либо фиксированную первообразную этой функции.
Таким образом, ДУ первого порядка (5) имеет бесконечно много решений вида
у= 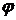 (х,С). (х,С).
| (8) |
Решение вида (8) называют общим решением уравнения (5).
Далее покажим, что для уравнения (2) при довольно общих рассуждениях относительно функции f(x,y) существует бясконое множество решений
|
|
|
у= 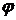 (х,С), (х,С),
| (9) |
где С – произвольная постоянная из некоторой области изменения (С), которое называют общим решением уравнения (2).
Решение, которое получено из общего решения (9) при конкретном значении С называется частным решением.
Решение, которое нельзя получить из общего решения ни при каком значении С, называют особым решением.
Соотношение вида Ф(x,y,C)=0, которое неявно определяет общее решение, называется общим интегралом дифференциального уравнения первого порядка (2).
Пример 1. Показать, что функция у2-х2-Су=0 является общим решением дифференциального уравнения у'(х2+у2) -2ху=0.
Решение.Найдём производную по х данной функции, заданой неявно. Таким образом получим:
2уу'-2х-Су'=0, у'(2у-С)=2х, 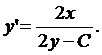
Из уравнения у2-х2-Су=0 находим С= (у2-х2)/у. Подставим значение С в формулу для вычисления у':
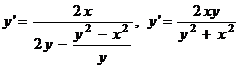 .
.
Тогда из уравнения у'(х2+у2) -2ху=0 и формулы для вычисления у' получим:
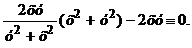
Таким образом, функция, заданная неявно у2-х2-Су=0, и зависящая от одной произвольной постоянной С, является решением дифференциального уравнения, т.е. является общим решением данного уравнения.
Пример 2.Найти дифференциальное уравнение семейства кривых у=Сх3.
|
|
|
Решение. Найдём производную данной функции, получим у'=3Сх2. Т.к. у=Сх3, то С=у/х3. Таким образом, находим дифференциальное уравнение
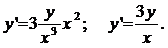
Часто требуется найти только решения, удовлетворяющие некоторым дополнительным условиям, например, найти решение уравнения (2) у=у(х), для которого у0=у(х0), где х0 и у0 заданные числа, называемые начальными значениями, условие у(х0)=у0 – начальное условие. Такая задача имеет специальное название – задачи Коши, т.е. задача Коши – это система, состоящая из ДУ и начального условия 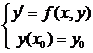 .
.
С геометрической точки зрения задача Коши означает: найти интегральную кривую, которая проходт через данную точку (х0,у0).
Пример 3.На плоскости хOу найти кривую, которая в каждой точке имеет касательную, угловой коэффициент которой равен удвоенной абсциссе точки касания.
Решение.Пусть у(х) – функция, графиком которой является искомая кривая. Известно, что угловой коэффициент касательной в точке М(х,у(х)) равен у'(х), с учётом условия задачи он равен 2х, то есть у'(х)=2х. Отсюда следует, что искомая функция является решением дифференциального уравнения у'=2х. Найдём интеграл этого уравнения. Множество всех решений дифференциального уравнения у'=2х является множеством всех первообразных для функции 2х, поэтому оно задается следующей формулой: у=х2+С, где С – произвольная постоянная. Графиком этих решений будут параболы. Их целое семейство. Задача решена. Выделим теперь из полученного семейства ту параболу, которая праходит через точку (1;2). Будем считать, что х=1, у=2. Тогда получим: 2=1+С, С=1. Значение С=1, которое нашли, падставим в уравнение у=х2+С. Таким образом получим, что у=х2+1 – уравнение искомой параболы.
|
|
|
Замечание.Мы рассмотрели одну геометрическую задачу, которая приводит к ДУ.
Возникает вопрос: при каких условиях задача Коши имеет решение и когда такое решение только одно.
Дата добавления: 2018-08-06; просмотров: 227; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
