Будем рассматривать вопрос существования и единственности решения
у= 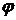 (х,С) (х,С)
| (8) |
|
|
с начальными значениями х=х0 и у=у0. Условие единственности означает следующее: если у1(х) и у2(х) – решения (2), которые определены на интервалах I 1 и I 2 соответственно, и которые удовлетворяют начальным условиям у1(х0)=у2(х0)=у0, тогда у1(х)=у2(х) на пересечении интервалов I 1 и I 2. С геометричной точки зрения это означает, что через каждую точку соответствующей области проходит интегральная кривая и причём только одна (см. рисунок).
§ 3. Существование и единственность решения
дифференциального уравнения первого порядка
Первое доказательствоательство существования и единственности решения дифференциального уравнения при заданных начальных условиях принадлежит Коши, которое он получил в 1820–1830 гг.
Теорема Пикара. Пусть дано уравнение
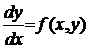
| (1) |
и начальные значэния х0, у0. Если функция f(x,y) удовлетворяет условиям:
1) является непрерывной по двум переменным в замкнутой области D. Тогда из свойства непрерывной в замкнутой области функции следует её ограниченность, т.е.  М>0, что |f(x,y)|
М>0, что |f(x,y)|  M
M 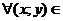 D;
D;
2) удовлетворяет в области D условию Липшица по переменной у, т.е 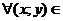 D выполняется неравенство|f(x,y1 )-f(x,y2 )|
D выполняется неравенство|f(x,y1 )-f(x,y2 )|  L|y1-y2|, где L– постоянная Липшица.
L|y1-y2|, где L– постоянная Липшица.
Тогда существует единственное решение у(х), которое удовлетворяет начальному условию
| у(х0)=у0 | (2) |
причём функция у(х) непрерывно дифференцируемая для всех х из отрезка
|x-x0 |  h, где h=min{a; b/M}, где а,b некоторые известные положительные числа, определяемые областью V Í D (см. док-во, 1 этап) и график у(х) принадлежит D для этих х.
h, где h=min{a; b/M}, где а,b некоторые известные положительные числа, определяемые областью V Í D (см. док-во, 1 этап) и график у(х) принадлежит D для этих х.
|
|
|
Лемма. Если функция f(x, y) в области D имеет ограниченную частную производную по у, то она удовлетворяет условия Липшица по второй переменной.
Доказательствоательство. По теореме Лагранжа
f(x, y1) – f(x, y2) = f¢y(x, y2 + q(y1 – y2))(y1 – y2), где 0< 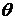 <1.
<1.
по условию леммы |f¢y(x, y)| £ L, " (x, y) Î D, тогда " (x, y1) Î D, " (x, y2) Î D имеем |f(x, y1) – f(x, y2)| £ L |y1 – y2|.
Доказательствоательство теоремы Пикара
Идея доказательствоательства. Доказательствоательство проведём в несколько этапов:
1) Построим вспомогательное интегральное уравнение.
2) Построим специальную последовательность функций, которые называют приближёнными решениями, и докажем их свойства.
3) Найдём предел последовательности приближённых решений с помощью признака Вейерштрасса равномерной сходимости функционального ряда.
 4) Покажем, что предел последовательности приближённых решений является решением задачи Коши.
4) Покажем, что предел последовательности приближённых решений является решением задачи Коши.
5) Докажем единственность найденного решения.
1). Сузим область D. Будем рас-сматривать ДУ (1) в замкнутой области V Í D, где
V = {(x,y)||x-x0|  a, |y-y0|
a, |y-y0|  b}( а,b некоторые известные положительные числа) – прямоугольник с центром в точке (x0, y0).
b}( а,b некоторые известные положительные числа) – прямоугольник с центром в точке (x0, y0).
|
|
|
Решение задачи Коши сводится к решению эквивалентного интеграль-ного уравнения
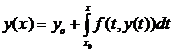 . (3)
. (3)
Действительно, уравнение (3) получается из (1) если его проинтегри-ровать по x на промежутке от x0 до x (|x – x0| £ a)
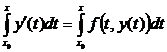 ,
,
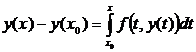
и воспользоваться начальным условием (2), то из
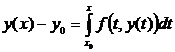
получаем уравнение (3).
Из интегрального уравнения (3) уравнение (1) получается при диффе-ренцировании его по x, а начальное условие (2) — подстановкой x = x0.
2). Построим последовательность функций
y0(x), y1(x), y2(x) … (4)
заданных на отрезке x0 – a £ x £ x0 + a, по следующему правилу
y0(x) º y0,
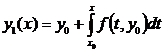 ,
,
 ,
,
...
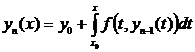 ,
,
...
Определение.Функции последовательности (4) называются приближёнными значениями задачи Коши (1), (2).
Выясним, какими свойствами обладают функции последовательности (4). В области V функция f(x, y) непрерывная, поэтому  M Î R, что|f(x, y)| £ M.
M Î R, что|f(x, y)| £ M.
Будем считать, что
x Î I = { |x – x0| £ h, дзе h = min{a, 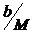 } }
} }
Покажем, что " x Î I, " i = 1, 2, … справедливы утверждения:
а) функции yi(x) непрерывные;
б) yi(x0) = y0;
в) |yi(x) – y0| £ b. (5)
Действительно:
|
|
|
а) функция y0(x) º y0 — непрерывная,  функция
функция 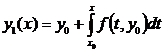 непрерывная, как сумма и композиция непрерывных функций и т.д.
непрерывная, как сумма и композиция непрерывных функций и т.д.
б) равенство yi(x0) = y0; получаем непосредственно подстановкой x = x0 в выражения для yi(x)
в) функция y0(x) очевидно удовлетворяет неравенству (5), далее используем метод математической индукции.
Для i = 1 из формулы для y1(x) имеем
|y1(x) – y0| = 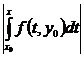 £
£ 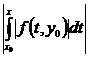 £
£
£ M 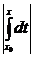 = M|x – x0| £
= M|x – x0| £ 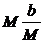 = b Þ (5)
= b Þ (5)
Предположим, что неравенство (5) выполняется для i = n – 1
|yn – 1(x) – y0| £ b (5¢)
Покажем справедливость (5) для i = n
|yn(x) – y0| = 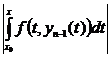 £ Ä
£ Ä
т.к. неравенство (5¢) выполняется, и точка (t, yn – 1(t)) при t Î I принадлежит области V, где функция f(x, y) ограниченная. Поэтому
Ä £ M 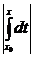 = M|x – x0| £
= M|x – x0| £ 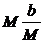 = b Þ (5)
= b Þ (5)
3). Покажем, что существует предел последовательности (4), причём последовательность сходится равномерно на I = { |x – x0| £ h }.
Построим функциональный ряд
y0(x) + [y1(x) – y0(x)] + [y2(x) – y1(x)] + … + [yn(x) – yn – 1(x)] + … (6)
последовательность частичных сумм которого — Sn(x) = yn(x).
Докажем что (6) сходится равномерно, тогда по определению равномерно сходящегося ряда последовательность {Sn(x)}, а значит и последовательность (4) будут равномерно сходящимися.
Оценим члены ряда (6): [y1(x) – y0(x)] мы уже рассматривали:
|
|
|
|y1(x) – y0(x)| £ 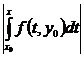 £ M|x – x0| (7)
£ M|x – x0| (7)
Для следующего члена (6) получаем
|y2(x) – y1(x)| = 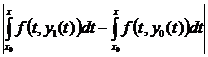 £
£
£  £ | воспользуемся условием Липшица | £
£ | воспользуемся условием Липшица | £
£  £ | используем (7) | £
£ | используем (7) | £
£  =
=  (8)
(8)
Аналогично
|y3(x) – y2(x)| = 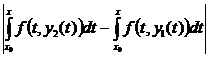 £ | условие Липшица | £
£ | условие Липшица | £
£ 
 £
£
£  =
=  .
.
По гипотезе математической индукции, пусть верно
|yn –1 (x) – yn – 2(x)| £ 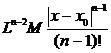 . (9)
. (9)
Тогда
|yn(x) – yn – 1(x)| = 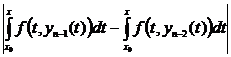 £ | условие Липшица | £
£ | условие Липшица | £
£ 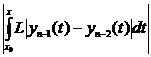
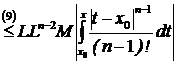 =
= 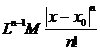 (10)
(10)
Таким образом, "x Î I = { |x – x0| £ h} получили последовательность оценок
(7) Þ |y1(x) – y0(x)| £ Mh
(8) Þ |y2(x) – y1(x)| £ 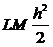
(9) Þ |yn –1 (x) – yn – 2(x)| £  .
.
(10) Þ |yn(x) – yn – 1(x)| £ 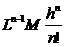
Тогда члены функционального ряда (6) не превосходят соответствующие члены знакоположительного числового ряда
y0 + Mh + 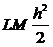 + ... +
+ ... +  +
+  + ... (11)
+ ... (11)
По признаку Д’Аламбера ряд (11) сходится
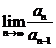 =
=  =
= 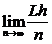 = 0 < 1
= 0 < 1  (11) – мажорантный
(11) – мажорантный 
 (по признаку Вейерштрассе) (6) сходится равномерно, а значит
(по признаку Вейерштрассе) (6) сходится равномерно, а значит  функция
функция
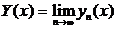 ,
,
причём Y(x) непрерывная на I (т.к. члены ряда – непрерывные).
Замечание. 1). Функция Y(x) удовлетворяет начальному условию (2).
Действительно,
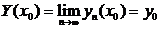 .
.
2). График функции Y(x) принадлежит области V.
Действительно, переходя в неравенстве (5) к пределу, при n ® ¥ получаем
|yi(x) – y0| £ b Þ |Y(x) – y0| £ b
4). Покажем, что функция Y(x) является решением уравнения (3).
По определению
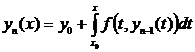 (12)
(12)
Считаем, что n ® ¥, тогда слева в (12)
 .
.
Пкажем, что справа в (12)
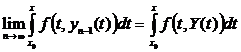 ,
,
это эквивалентно
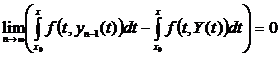 . (13)
. (13)
Распишем  по определению по Коши:
по определению по Коши:
"e > 0, $N(e) Î N ,`"n ³ N(e), "xÎ I Þ |yn(x) – Y(x)| < e. (*)
Пусть n – 1 ³ N(e), оценим модуль разности

(используем условие Липшица)
 . (14)
. (14)
Тогда "e1 > 0 можно найти e = e1/Lh и из (*) найти N(e)Î N такое, что (14) будет выполняться "n ³ N(e), "xÎ I 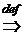 (13).
(13).
Таким образом, предельный переход в (12), при n ® ¥, приводит к равенству
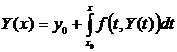 , (15)
, (15)
причём функция Y(x) является непрерывно диффернцируемой по х.
5). Единственность докажем методом от противного.
Пусть существуют два решения задачи Коши Y(x) и Z(x), которые не совпадают ни в какой окрестноститочки x0 , т.е. Y(x) ¹ Z(x).
Рассмотрим 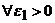 и e>0 такое, что [x0, x0 + e]
и e>0 такое, что [x0, x0 + e] 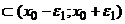 . Всилу непрерывности функций Y(x) и Z(x) на отрезке [x0, x0 + e] существует точка x1, что
. Всилу непрерывности функций Y(x) и Z(x) на отрезке [x0, x0 + e] существует точка x1, что
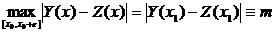 .
.
Тогда
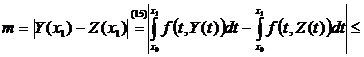
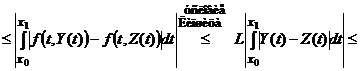
 .
.
Получили неравенство
m £ Lme Þ 1 £ Le. (16)
Но e — произвольное положительное число, поэтому неравенство (16) выполняется не всегда.
Теорема доказательствоана.
Метод изоклин
1º. Поле направлений ОДУ первого порядка.
Рассмотрим геометрическую интерпритацию ОДУ первого порядка
y¢ = f(x, y) (1)
Считаем, что правая часть f(x, y) задана в некоторой области D плоскости XOY. Это означает, что в каждой точке (x, y) Î D функция f(x, y) определена и имеет значение.
Сдругой стороны из (1) следует, что значение функции f(x, y) есть значение производной решения (функции у(х)) в точке x. Геометрически значение y¢ есть угловой коэффициент касательной к графику решения (интегральной кривой) относительно оси OX или направление. На плоскости направление можно обозначать небольшой чертой или стрелкой. В каждой точке области — своё направление.
Таким образом ОДУ задаёт на координатной плоскости поле направлений.
2º. Понятце изоклины.
Если поле направлений построено, то интегральная кривая — это кривая, которая в каждой точке области D имеет касательную с направлением, совпадающим с направлением поля в этой точке.
Строить поле направлений можно несколькими способами (вручную, с помощью компьютера).
В первом случае используют так называемые изоклины.
Определение. Изоклина — это кривая в поле направлений со следующим свойством: во всех точках кривой поле имеет одно и тоже направление.
Для ОДУ y¢ = f(x, y) фиксированое значение направления — это фиксированое значение производной y¢ = k. Таким образом, изоклину задаёт равенство k = f(x, y).
Отсюда следует, что изоклины ОДУ y¢ = f(x, y) — это линии уровня функции f(x, y).
Обычно с помощью изоклин строят поле направлений, а потом строят интегральные кривые.
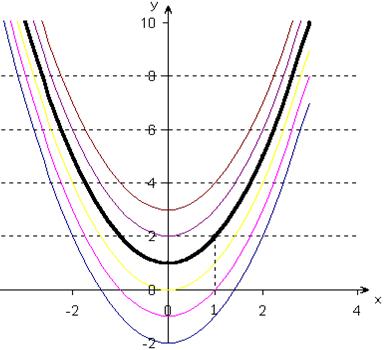
Пример. Построить с помощью изоклин поле направлений, которое задаёт ДУ 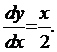
Решение. Уравнение семейства изоклин данного ДУ имеет вид k=x/2, или х=2k (прямые параллельные оси Оу).
Построим несколько изоклин. Для этого строим таблицу значений угла j (где j=arctg k) и уравнений изоклин для соответствующего k:
| k=x/2 | x=2k | 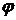 =arctgk =arctgk
|
| k=0 | x=0 | 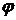 =0 =0
|
| k=1 | x=2 | 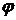 =π/4 =π/4
|
| k=-1 | x=-2 | 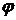 =-π/4 =-π/4
|
Чтобы найти интегральную кривую, надо взять какую-нибудь точку (х0,у0) на плоскости и провести через неё кривую таким образом, чтобы направление в каждой точке кривой совпадало с направлением поля. Получим семейство кривых (парабол) у=х2/4+С.
Дата добавления: 2018-08-06; просмотров: 250; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!