Дифференциальные уравнения первого порядка
Основные понятия. Примеры
В интегральном исчислении решалась задача о нахождении функции по её производной, т.е. найти функцию у(х), которая удовлетворяет на некотором промежутке I уравнению у'=f(x), где f – заданная функция.
Сформулируем более общую задачу: пусть F – заданная функция (n+2) переменных, и требуется найти функцию у(х), которая на некотором промежутке I удовлетворяет уравнению F( x, y(x), y'(x),…, y(n)(x))=0.
Определение 1.Уравнение, которое связывает неизвестную функцию с её независимыми переменными и с её производными называется дифференциальным уравнением (ДУ). Если неизвестная функция является функцией одной переменной (мы будем рассматривать случай действительной переменной), то такое ДУ назывется обыкновенным дифференциальным уравнением (ОДУ), т.е. ОДУназывается соотношение вида
| F(x,y(x),y'(x),…,y(n)(x))=0, | (1) |
где F – известная функция, х – независимая переменная, у(х) – неизвестная функция.
Замечание. Уравнение, в котором неизвестная функция является функцией нескольких переменных, называется уравнением с частными производными.
Определение 2.Порядком дифференциального уравнения называется порядок старшей производной неизвестной функции у= у(х), входящей в уравнение.
Пример 1. Определить порядок дифференциального уравнения:
1) y"-3у' +2y - 4=0;
2) x (1+x) y'-(1+2x) y-(1+2x)=0;
3) y(4)-16y"=0.
Решение.Первое уравнение является ДУ порядка, т.к. наивысший порядок производной неизвестной функции равен ; второе уравнение – порядка, последнее уравнение является уравнением порядка, т.к. наивысший порядок производной неизвестной функции равен
|
|
|
Определение 3.Функция у(х) называется решением дифференциаль-ного уравнения, если она n раз непрерывно дифференцируемая на некотором промежутке I и, если хОI, то функция у(х) удовлетворяет уравнению (1).
Пример 2.Показать, что функция y=sinx является решением дифферен-циального уравнения у"+у = 0 на множестве действительных чисел R.
Решение. Найдём производную второго порядка функции y=sinx:
y'=cosx, y"=-sinx, где хОR.
Подставим выражения для y и у" в дифференциальное уравнение,
у"+у=-sinx+sinx=0. Это значит, что функция у=sinx является решением данного дифференциального уравнения. Можно показать, что данное дифференциальное уравнение на множестве R имеет ещё решение y=cosx. А также, что решением данного дифференциального уравнения является любая функция, определяемая формулой:
у=C1sinx+C2cosx, где С1 и С2 некоторые произвольные постоянные.
Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.
Определение 4. График решения дифференциального уравнения называется интегральной кривой этого уравнения.
|
|
|
Многие задачи естествознания приводят к решению дифференциальных уравнений. Рассмотрим некоторые из них.
Задача о движении материальной точки массы m под действием внешних сил.
Это движение описывается вторым законом Ньютона: ma=F.
Пусть точка движется по оси Ох и x(t) – её абсцисса в момент времени t. Тогда функция x(t) удовлетворяет дифференциальному уравнению второго порядка
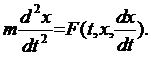
| (2) |
Если точка движется в трёхмерном пространстве и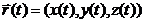 
– её радиус-вектор, то
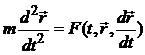
Это соотношение – система трёх обыкновенных дифференциальных уравнений с тремя неизвестными функциями x(t), y(t), z(t).
Чтобы найти положение точки в момент времени t необходимо, как известно из механики, знать её положение и скорость в некоторый начальный момент времени t0. Поэтому, чтобы найти решение уравнения Ньютана (2) неабходимо задать начальные условия
| x(t0)=x0, | 
|
Замечание.Когда задачу нахождения всех решений дифференциаль-ного уравнения удается свести к вычислению конечного числа интегралов и производных от известных функций, а также к алгебраическим операциям над ними, то говорят, что уравнение интегрируется в квадратурах. Класс этих функций очень узок.
|
|
|
Например, уравнение (2) интегрируется в квадратурах только если правая часть уравнения – функция F, зависит только от одной переменной:
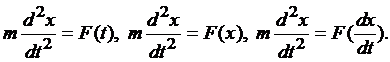
Пример 3. Является ли дифференциальное уравнение у'=sinx/x интегрируемым в квадратурах.
Решение.Множество всех решений данного дифференциального уравнения задается формулой 
где С – произвольная постоянная. Получили, что данное уравнение интегрируется в квадратурах.
Пример 4.ДУ y¢ = x2 + y2 не интегрируется в квадратурах.
Задачей теории обыкновенных дифференциальных уравнений является нахождение решений дифференциальных уравнений, исследование общих свойств решений и развитие точных, асимптотических и численных методов интегрирования дифференциальных уравнений.
Дифференциальные уравнения первого порядка
Общий вид ДУ первого порядка
| F(x,y,y')=0 . | (1) |
Частным случаем уравнения (1) является уравнение
 ,
| (2) |
где действительная функция f(x,y) задана в некоторой области D(х,у). Тогда говорят, что дифференциальное уравнение (2) задано в области D(х,у). Дифференциальное уравнение (2) – это уравнение разрешимое относительно производной.
Если в окрестности точки (х,у) функция f(х,у) обращается в бесконечность, то наравне с уравнением (2) рассматривают уравнение вида
|
|
|
 .
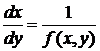| (2’) |
Кроме того уравнение (2’) целесообразно рассматривать, если оно легче разрешимо, чем ДУ (2).
Дата добавления: 2018-08-06; просмотров: 197; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!