Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами

1º. Характеристическое уравнение

Рассмотрим ЛОДУ n-го порядка с постоянными действительными коэффициентами

y⁽ⁿ⁾ + p₁y⁽ⁿ^{– 1}⁾ + p₂y⁽ⁿ^{– 2}⁾ +… + p_n_{– 1}y¢ + p_ny = 0 " x Î R.                     (1)

Для нахождения общего решения ЛОДУ (1) надо найти систему n линейно независимых решений (1).

Обычно решения ЛОДУ (1) находят в форме

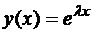,                                                            (2)

где l — неизвестная константа.

Если подставить (2) в (1), получаем

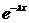lⁿe^l^x + p₁lⁿ^{– 1} + p₂lⁿ^{– 2} +… + p_n_{– 1}l + p_n = 0,   | ¹ 0

lⁿ + p₁lⁿ^{– 1} + p₂lⁿ^{– 2} +… + p_n_{– 1}l + p_n = 0.                               (3)

Очевидно, что имеет место

Лемма 1. Для того, чтобы функция (2) была решением ЛОДУ (1) неабходимо и достаточно, чтобы l было корнем уравнения (3).

Определение. Уравнение (3) называется характеристическим уравнением (ХР) ЛОДУ (1).

Рассмотрим подробно ЛОДУ 2-го порядка с постоянными действительными коэффициентами

L(y) º y² + py¢ + qу = 0.                                          (4)

Для ЛОДУ (4) ХР будет иметь иметь вид

l² + pl + q = 0.                                                     (5)

Выводы, полученные для ЛОДУ (4), можно перенести на ЛОДУ (1) n-го порядка.

Известно, что уравнение (5) имеет два корня с учётом кратности.

Рассмотрим всевозможные случаи:

1) корни действительные и различные,

2) корни комплексные,

3) корень действительный, кратности 2.

2º. Случай различных действительных корней

Пусть l₁, l₂ Î R корни ХР (5) и l₁ ¹ l₂.

Тогда решения ЛОДУ (4) имеют вид

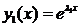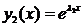, .                                            (6)

Они линейно независимые (§ 13, п. 2º,пример 3), поэтому образуют линейно независимую систему функций, т. е. фундаментальную систему решений (4).

Тогда общее решение ЛОДУ (4) имеет вид

.

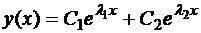Замечание. Аналогичный (6) вид имеют решения ЛОДУ (1) n-го порядка в случае различных действительных корней ХР.

3º. Случай комплексных корней

Пусть l₁ = a + ib — комплексный корень ХР (5).

Поскольку коэффициенты ХР — действительные числа, ХР должно иметь второй комплексный сопряжённый корень l₂ = a – ib.

Таким образом ЛОДУ (4) должно иметь два комплексных решения

, .

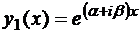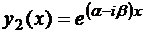Убедимся в этом.

Определение. Фукция z(x) = u(x) + iv(x), где u(x) и v(x) — действительные функции от действительной переменной x, называется комплексной функцией от действительной переменной.

u(x) — называется действительной частью z(x), v(x) — мнимой частью, 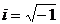– мнимая единица.

Имеет место

Лемма 2. Если в формуле z(x) = u(x) + iv(x)

функции u(x) и v(x) действительные и n раз дифференцируемые, тогда

z⁽ⁿ⁾(x) = u⁽ⁿ⁾(x) + iv⁽ⁿ⁾(x).                                       (7)

Без доказательства.

Найдём действительную и мнимую части комплексных функций y₁, y₂. Для этого воспользуемся формулой Эйлера, которая определяет e в комплексной степени

e^ix = cos x + isin x.                                                 (8)

Тогда

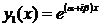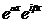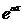= = (cosbx + isinbx) = 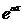cosbx + i 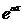sinbx = u(x) + iv(x),

где u(x) = 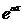cosbx, v(x) = 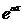sinbx.

Аналагично

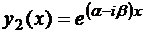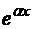= cosbx – i 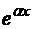sinbx.

Лемма 3. При любом комплексном a имеет место формула

(e^ax)¢ = ae^ax.

Без доказательства.

Легко убедиться, что функции

, .

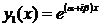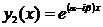являются рашениями ЛОДУ (4), причём являются комплексными сопряжёнными функциями.

Найдём соответствующие действительные решения ЛОДУ (4).

Имеет место

Теорема 1. Если ЛОДУ (4) с действительными коэффициентами имеет комплексный корень z(x) = u(x) + iv(x), тогда действительная и мнимая части этого решения являются решениями (4).

Доказательство. Воспользуемся линейностью оператора L. Пусть

L(z) = 0. Тогда L(z) = L(u + iv) = L(u) + iL(v) = 0, отсюда следует, што

L(u) = 0, L(v) = 0.

Теорема доказана.

Решения y₁, y₂ имеют практически одинаковую действительную и мнимую части, поэтому паре комплексных сопряжённых решений (4)

,

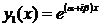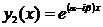
соответствует пара действительных решений

u(x) = 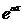cosbx, v(x) = 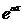sinbx.                                       (9)

Лемма 4. Функции u(x) = 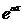cosbx, v(x) = 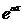sinbx образуют линейно независимую систему.

Доказательство. Надо определиться с подбором постоянных a₁, a₂ в равенстве a₁ 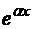cosbx + a₂ 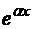sinbx = 0.

Поскольку 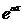¹ 0, то это равенство равносильно

a₁cosbx + a₂sinbx = 0.

Таким образом, линейная независимость системы функций 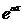cosax, 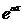sinbx эквивалентна линейной независимости системы функций cosax, sinbx.

Строим вронскиан = b ¹ 0.

Лемма доказана.

Общее решение ЛОДУ (4) в данном случае имеет вид

y(x) = 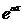(C₁cosbx + C₂sinbx).

Замечания

1). Если корни ХР (5) имеют вид l_1,2 = ±ib (a = 0), то общее решение имеет вид y(x) = C₁cosbx + C₂sinbx.

2). Аналагичный (9) вид имеют решения ЛОДУ (1) n-го порядка в случае комплексных корней кратности 1.

4º. Случай кратного действительного корня

Теорема 2. Если l — корень ХР (5) кратности 2, тогда функции

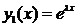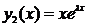,                                              (10)

являются фундаментальной системой решений ЛОДУ (4).

Доказательство. Функция 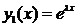является решением (4) по Лемме 1.

Покажем (самостоятельно), что функция 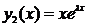— также решение (4).

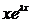Проверяем линейную независимость. Надо определиться с постоянными a₁, a₂ в равенстве a₁ + a₂ = 0.

Поскольку ¹ 0, то это равенство равносильно равенству

a₁×1 + a₂×x = 0,

а линейную независимость системы функций 1, x мы доказали (§ 13, п. 1º, пример 2).

Теорема доказана.

В рассматриваемом случае общее решение ЛОДУ (4) имеет вид

y(x) = C₁ 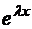+ C₂ .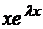

Замечания

1). Если ХР ЛОДУ (1) n-го порядка имеет действительный корень l кратности k , то этому корню соответствуют k решений ЛОДУ вида

, , ... , .

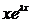2). Если ХР ЛОДУ (1) n-го порядка имеет комплексный корень

l = a + ib кратности k, то этому и сопряжённому корням соответствуют 2k решений ЛОДУ вида

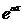cosbx, 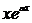cosbx, ... , 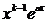cosbx,

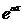sinbx, 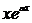sinbx, ... , 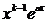sinbx.

Дата добавления: 2018-08-06; просмотров: 244; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 6 7 8910 11 Следующая ⇒

Мы поможем в написании ваших работ!