Дифференциальные уравнения n–ого порядка
1º. Основные определения
Обыкновенные дифференциальные уравнения n–ого порядка записываются в виде
F(x, y(x), y¢(x), …, y(n)(x)) = 0, x Î I. (1)
Чаще всего встречаются ДУ разрешённые относительно старшей производной
y(n) = f(x, y, y¢, …, y(n–1)), x Î I (2)
Определение 1. Решением ОДУ(2) на промежутке Iназывается функция, которая непрерывно дифференцируемая n раз на этом промежутке и удовлетворяет на нём уравнению (2).
Для уравнения (2) задача Коши задаётся с помощью нескольких начальных условий
y(x0) = y0
y¢( x0) =  (3)
(3)
…
y(n – 1)( x0) = 
где y0,  , …,
, …,  — начальные значения решения.
— начальные значения решения.
Теорема существования и единственности решения (достаточное условие). Пусть дана задача Коши (2), (3), и функция f(x, y, y¢, …, y(n–1)) определенная в некоторой замкнутой области D пространства Rn+1 с точками (x, y, y¢, …, y(n–1)), и область D содержит точку (x0, y0,  , …,
, …,  ).
).
Если в области D функция f(x, y, y¢, …, y(n–1)) непрерывная по всем аргументам и имеет ограниченные производные по y, y¢, …, y(n–1), тогда задача Коши (2), (3) имеет на некотором промежутке по x единственное решение.
Без доказательства.
2º. Виды решений и интегралов
Определение. Общим решением ОДУ (2) называется функция
y = j(x, C1, C2, ... , Cn), (4)
|
|
|
которая определена в некоторой области измянения аргументов, имеет непрерывные частковыя производные по x до порядка n включительно, причём
1) система уравнений
 (5)
(5)
разрешима относительно C1, C2, ... , Cn , т.е. существует система уравнений
 (6)
(6)
2) во всех точках (x, y, y¢, …, y(n–1)) области D система (6) определяет значэнния C1, C2, ... , Cn (включая ±¥), при которых функция (4) является решением ОДУ (2).
Определение. Общим интегралом ОДУ (2) называется соотношение вида F(x, y, C1, C2, ... , Cn) = 0, которое неявно задаёт общее решение ОДУ (2).
Определение. Частныминтегралом ОДУ (2) называется выражение для общего интеграла с конкретными значениями произсвободных констант.
Дифференцыяльные уравнения, допускающие понижение порядка
1º. Уравнения, допускающие непосредственное интегрирование
Рассмотрим ОДУ n-го порядка вида
y(n) = f(x). (1)
Правая часть зависит только от переменной x.
Чтобы найти общее решение, нужно только проинтегрировать n раз.
Пример 1. y²¢ = cos x.
Имеем y² = sin x + C1,
|
|
|
y¢ = –cos x + C1x + C2,
y = –sin x + C1x2 + C2x + C3.
2º. Уравнения, не содержащие явно искомую функцию у
Рассмотрим ОДУ второго порядка общего вида
F(x, y¢, y²) = 0. (2)
Порядок уравнения можна понизить подстановкой
y¢(x) = z(x),
где z(x) — новая неизвестная функция.
Так как y² = z¢, то после подстановки имеем
F(x, z, z¢) = 0.
Это уравнение первого порядка и нужно найти общее решение
z = j(x, C1).
Потом подстановка y¢(x) = z(x) рассматривается как уравнение
y¢(x) = j(x, C1),
из которого находим общее решение уравнения (2).
Аналогично, порядок ОДУ вида
F(x, y(k), y(k+1), …, y(n)) = 0
можно понизить подстановкой
y(k)(x) = z(x).
Пример 2. y²(x2 + 1) = 2xy¢.
Подстановка y¢(x) = z(x), поэтому y² = z¢ и имеем уравнение
z¢(x2 + 1) = 2xz.
 , z ¹ 0 (!)
, z ¹ 0 (!)
ln|z| = ln|x2 + 1| + ln|C1|, C1 ¹ 0
z = C1(x2 + 1), C1 ¹ 0
но (!) z = 0 — решение, поэтому добавим C1 = 0.
Строим новое уравнение
y¢ = C1(x2 + 1)
Непосредственным интегрированием получаем общее решение
 .
.
3º. Уравнения, не содержащие явно независимую переменную х
Рассмотрим ОДУ второго порядка общего вида
F(y, y¢, y²) = 0. (3)
Порядок уравнения можно понизить подстановкой
y¢ = z(y),
|
|
|
где z(y) — новая неизвестная функция.
Находим выражения для
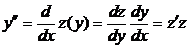 .
.
После подстановки имеем
F(y, z, z¢z) = 0.
Это уравнение первого порядка, где y независимая переменная, а z — искомая функция. Находим его общее решение
z = j(y, C1),
из подстановки строим новое уравнение
y¢ = j(y, C1),
из которого находим общее решение исходного уравнения.
Аналогично можно понизить на единицу порядок уравнений вида
F(y, y¢, …, y(n)) = 0.
Пример 3. yy² – (y¢)2 = 0.
Используем замену
y¢ = z(y), y² = z¢z :
yz¢z – z2 = 0,
 , y ¹ 0, z ¹ 0 (!)
, y ¹ 0, z ¹ 0 (!)
ln|z| = ln|y| + ln|C1|, C1 ¹ 0
z = C1y, C1 ¹ 0,
но (!) z = 0 — решение, поэтому добавляем C1 = 0.
z = C1y,
Возвращаемся к переменной y
y¢ = C1y, 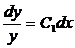 ,
,
ln|y| = C1x + ln|C2|, C2 ¹ 0,
 , C2 ¹ 0,
, C2 ¹ 0,
но (!)y = 0 — решение, поэтому добавляем C2 = 0.
Вывод:  ,
, 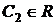
Дата добавления: 2018-08-06; просмотров: 439; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
