Вопрос 19. Метод наименьших квадратов (МНК). Свойства оценок МНК.

Для того, чтобы полученные методом наименьших квадратов оценки обладали желательными свойствами делаются следующие предположения об отклонениях ε_i:

1. Величина ε_i – случайная переменная;

2. Математическое ожидание ε_i равно 0;

3. Дисперсия ε_i постоянна для всех i-тых ε;

4. Значения ε_i не зависимы между собой.

Известно, что если условия (1-4) выполняются, то оценки, вычисляемые с помощью МНК (метода наименьших квадратов) обладают следующими свойствами:

1. Оценки являются несмещенными, то есть математическое ожидание оценки каждого параметра равно его истинному значению. Это вытекает из того, что математическое ожидание ошибки равно 0 и говорит об отсутствии системной ошибки в определении положения линии регрессии.

2. Оценки состоятельны, так как дисперсия оценок параметров при росте числа наблюдений стремится к 0. Иначе говоря, если n достаточно велико, то практически наверняка растет надежность оценки параметров а_j.

3. Оценки эффективны, то есть имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров.

Перечисленные свойства не зависят от конкретного вида распределения величины e, тем не менее, обычно предполагается, что они распределены нормально. Эта предпосылка необходима для проверки статистической значимости сделанных оценок и определения для них доверительных интервалов. При ее выполнении оценки МНК имеют наименьшую дисперсию не только среди линейных, но и среди всех несмещенных оценок.

Возможны разные виды уравнений множественной регрессии: линейные и нелинейные.

Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. В линейной множественной регрессии

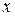параметры при называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Рассмотрим линейную модель множественной регрессии . (2.1)

Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного

признака от расчетных минимальна:

. (2.2)

Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю. Имеем функцию аргумента:

.

Находим частные производные первого порядка:

После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии (2.1):

Для двухфакторной модели данная система будет иметь вид:

Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:

(2.4)

где 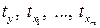– стандартизированные переменные: , , 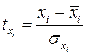для которых среднее значение равно нулю: , а среднее квадратическое отклонение равно единице: ; – стандартизированные коэффициенты регрессии.

Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии можно сравнивать между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой. Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида

(2.5)

где и – коэффициенты парной и межфакторной корреляции.

Коэффициенты «чистой» регрессии 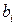связаны со стандартизованными коэффициентами регрессии следующим образом:

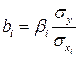. (2.6)

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (2.4) к уравнению регрессии в натуральном масштабе переменных (2.1), при этом параметр определяется как

.

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением .

На основе линейного уравнения множественной регрессии

(2.7) могут быть найдены частные уравнения регрессии:

(2.8)

т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором при закреплении остальных факторов на среднем уровне. В развернутом виде систему (2.8) можно переписать в виде:

При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем

(2.9)

где

В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:

, (2.10)

где 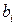– коэффициент регрессии для фактора в уравнении множественной регрессии, – частное уравнение регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности:

, (2.11)

которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

Вопрос 20. Методы оценивания линейной модели множественной регрессии в Excel.

(*)

Модель (*) – линейная эконометрическая модель в виде изолированных уравнений с несколькими объясняющими переменными или моделями линейной множественной регрессии.

В этой модели две экзогенные переменные x1, x2 и одна эндогенная переменная y. Спецификация (*) содержит четыре параметра:

Пусть известны значения экзогенных и эндогенных переменных модели (*): при t=1, 2, …, n.

Порядок оценивания модели (*) состоит из следующих шагов.

Шаг 1. В столбце А листа Excel с первой строчки расположить значения эндогенной переменной y. В столбцах B и C, начиная с первой строчки, записать значения экзогенных переменных соответственно и .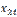

	A	B	C	D	E	F	G
	y1	X11	X21
	Y2	X12	X22
…	…	…	…
n	yn	X1n	X2n
n+1
n+2
n+3
n+4
n+5

Шаг 2. Активировать ячейку с адресом А(n+1) и на стандартной панели инструментов щелкнуть мышью кнопку вставки функций (f_x).

Шаг 3. В диалоговом окне «Категория» выбрать «Статистические»; в диалоговом окне «Выберите функцию» - «Линейн»; щелкнуть мышью по кнопке ОК.

Шаг 4. В строчке «Известные_значения_y» диалогового окна указать (латиницей!) адрес А1:Аn диапазона значений эндогенной переменной y_t, а в строчке «Известные_значения_х» - адрес B1:Cn диапазона известных значений предопределенных переменных x₁,x₂.

Шаг 5. В строчку «Конст» диалогового окна занести (кириллицей!) слово «истина», либо цифру 1.

Шаг 6. В строчку «Статистика» диалогового окна занести слово «истина» или цифру 1 и щелкнуть мышью по кнопке ОК.

Шаг 7. Выделить мышью диапазон ячеек A(n+1):C(n+5).

Шаг 8. Щелкнуть мышью по строке формул.

Шаг 9. Нажать клавиши Ctrl + Shift + Enter.

В итоге в выделенном диапазоне ячеек появятся результаты оценивания модели (*).

	A	B	C	D	E	F	G
	y1	X11	X21
	Y2	X12	X22
…	…	…	…
n	Yn	X1n	X2n
n+1
n+2
n+3			# Н/Д
n+4	F		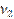# Н/Д
n+5			# Н/Д

Итак, модель будет выглядеть:

---

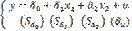
Дата добавления: 2018-08-06; просмотров: 2013; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!