T-статистика значимости оценки параметра регрессионной модели: формула, параметры для определения критического значения.

⇐ ПредыдущаяСтр 2 из 18Следующая ⇒

Спомощью метода наименьших квадратов мы получили лишь оценки параметров уравнения регрессии. Важной задачей на начальном этапе статистического анализа построенной модели является проверка значимости параметров регрессии. Чтобы проверить, значимы ли эти параметры (т.е. значительно ли они отличаются от нуля в «истинном» уравнении регрессии

y = a x + b), используют статистические методы проверки гипотез.

Предположим, что в качестве основной гипотезы Н₀ выдвигается гипотеза о незначимом отличии от нуля «истинного» коэффициента регрессии a: Н₀ = {a = 0}; альтернативной гипотезой Н₁ при этом является гипотеза о значимости данного коэффициента: Н₁ = {a ¹ 0}. Для проверки гипотезы Н₀ используется статистика

, (2.25)

Которая при справедливости Н₀ имеет распределение Стьюдента с (n – 2) степенями свободы (теорема 2.2). Следовательно, нулевая гипотеза Н₀: a = 0 отклоняется на основании t-критерия Стьюдента и принимается гипотеза о значимости коэффициента регрессии, если

Где a – требуемый уровень значимости, t_1–a/2(n – 2) – квантиль порядка (1–a/2) распределения Стьюдента с (n – 2) степенями свободы. При невыполнении данного неравенства считается, что нет оснований для отклонения Н₀.

По аналогичной схеме проверяется гипотеза о значимости свободного члена b. Для этого используется статистика

(2.26)

которая при справедливости нулевой гипотезы Н₀: b = 0 имеет распределение Стьюдента с (n – 2) степенями свободы (теорема 2.2). Следовательно, Н₀ отклоняется на основании t-критерия Стьюдента и принимается гипотеза о значимости свободного члена уравнения регрессии, если

где a – требуемый уровень значимости.

Замечание 2.2.При оценке значимости параметров линейной регрессии на начальном этапе можно использовать следующее грубое правило, позволяющее не прибегать к таблицам:

· если , то коэффициент регрессии a (свободный член b) не может быть признан значимым, так как соответствующая надежность составит менее 0,7;

· если , то параметр регрессии может рассматриваться как относительно (слабо) значимый: надежность в этом случае лежит между значениями 0,7 и 0,95;

· если , то это свидетельствует о значимости параметра регрессии: надежность в этом случае колеблется от 0,95 до 0,99;

· наконец, если , то это почти полная гарантия значимости параметра регрессии. 3

2.5.2. Оценка значимости уравнения регрессии

После проверки значимости каждого параметра модели обычно проверяется общее качество уравнения регрессии, которое оценивается по тому, насколько хорошо согласуется уравнение регрессии со статистическими данными. Проверить значимость уравнения регрессии – это значит установить, соответствует ли эконометрическая модель, выражающая зависимость между переменными, экспериментальным данным.

Мерой соответствия уравнения регрессии статистическим данным является коэффициент детерминации R², определяемый по формуле

(2.27)

Величина R² показывает, какая часть (доля) вариации (изменения относительно среднего значения) зависимой переменной объясняется уравнением регрессии, а, следовательно, и вариацией объясняющей переменной.

Исходя из определения (2.27), можно показать, что 0 £ R²£ 1.

Чем ближе R² к единице, тем теснее точки корреляционного поля примыкают к линии регрессии, тем лучше регрессия аппроксимирует эмпирические данные. Если R² = 1, то эмпирические точки (x_i, y_i), i = 1,2,…, n, лежат на линии регрессии и между переменными X и Y существует линейная функциональная зависимость: Y = aX + b , a ¹ 0. При ослаблении зависимости между переменными величина R² приближается к нулю. Если R² = 0, то вариация зависимой переменной полностью обусловлена воздействием случайных факторов, и линия регрессии параллельна оси абсцисс:

Однако не следует абсолютизировать высокое значение R². Коэффициент детерминации может быть близким к единице просто в силу того, что обе исследуемые величины X и Y имеют выраженный, например, временной тренд (т.е. зависимость от времени), не связанный с их причинно-следственной зависимостью. В экономике обычно такой тренд имеют объемные показатели (ВНП, ВВП, доход, потребление и т.п.). Поэтому при оценивании регрессий по временным рядам объемных показателей (например, зависимость потребления от дохода или спроса от цены) величина R² может быть весьма близкой к единице. Но это не обязательно свидетельствует о наличии значимой линейной связи между исследуемымипоказателями, а может означать лишь то, что поведение зависимой переменной нельзя описать уравнением

Проверка значимости (или адекватности эмпирическим данным) уравнения регрессии осуществляется с помощью F-статистики

. (2.28)

Если справедлива нулевая гипотеза Н₀ об отсутствии линейной зависимости между переменными X и Y, то статистика (2.28) имеет F-распределение Фишера с n₁ = 1 и n₂ = n –2 степенями свободы. Следовательно, на основании F-критерия Фишера с надежностью g = 1 – a принимается конкурирующая гипотеза Н₁ о наличии значимой линейной зависимости между переменными X и Y, если выполняется неравенство

где – квантиль порядка (1 – a) F-распределение Фишера с n₁ = 1 и n₂ = n – 2 степенями свободы.

Пример 2.4. По данным примера 2.2 оценить с надежностью 0,95 значимость параметров и уравнения построенной регрессии.

Решение. По формулам (2.25) и (2.26), используя результаты примеров 2.2 и 2.3, вычислим t-статистики:

Уровень значимости a = 1 – 0,95 = 0,05, табличное значение квантиля порядка 1 – a/2 = 0,975 равно t_{1 – a/2}(n – 2) = t_{0, 975}(10) = 2,228.

Поскольку (24,132 > 2,228), то нулевая гипотеза Н₀: a = 0 должна быть отвергнута в пользу альтернативной на уровне значимости 0,05. Это подтверждает статистическую значимость коэффициента регрессии.

Так как (0,76 < 2,228), то гипотеза о статистической незначимости коэффициента b не отклоняется. Это означает, что в данном случае свободным членом уравнения регрессии можно пренебречь, рассматривая регрессию как y = ax.

Рассчитаем коэффициент детерминации по формуле (2.27). Для этого нам понадобится значение (из примера 2.3). Кроме того, нам потребуется величина , которую вычислим аналогично тому, как нашли в примере 2.3:

Здесь мы воспользовались табл. 2.2. Тогда, в силу (2.27), имеем:

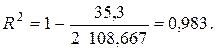
По формуле (2.28) вычисляем значение F-статистики:

По таблице 3 Приложения квантилей F-распределения находим

F_{1 – a}(1, n – 2) = F_0,95(1,10) = 4,96. Так как F > F_0,95(1,10) (291,596 > 4,96), то построенное уравнение регрессии значимо.

Отметим, что большое значение коэффициента детерминации (следовательно, и F-статистики) свидетельствует о высоком общем качестве построенной модели зависимости переменных X и Y. g

Замечание 2.3.Для коэффициента детерминации R² можно получить другое полезное представление:

. (2.29)

Формула (2.29) вытекает из (2.27), если воспользоваться важным в дисперсионном анализе разложением вариации (суммы квадратов отклонений от средних) зависимой переменной на вариацию, обусловленную линейным воздействием независимой переменной (т.е. уравнением регрессии), и вариацию, обусловленную случайным возмущением:

. 3

Дата добавления: 2018-08-06; просмотров: 6718; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!