Матричная форма метода наименьших квадратов: спецификация парной регрессионной модели в матричной форме.
Уравнение парной регрессии в матричной форме:
Y = X·A + ε ,
где Y – вектор-столбец (nx1) наблюдаемых значений зависимой переменной;
X – матрица (nx2) значений факторов;
A – вектор-столбец (2x1) неизвестных коэффициентов регрессии;
ε – вектор-столбец (nx1) ошибок наблюдений
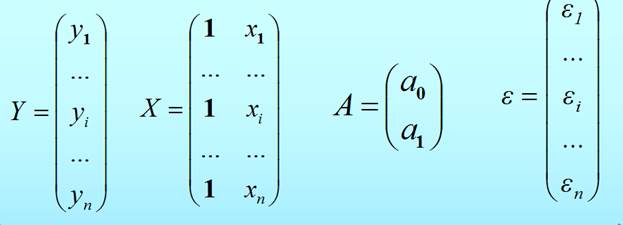
Параметры системы нормальных уравнений находятся с помощью МНК по формуле:
A = (X’·X)-1·X’·Y
Для расчета вектора A необходимо:
1. Транспонировать матрицу X => [ ТРАНСП];
2. Умножить транспонированную матрицу на исходную (X’X) => [МУМНОЖ];
3. Вычислить обратную матрицу (X’X)-1 => [МОБР];
4. Умножить обратную матрицу на транспонированную (X’·X)-1·X’ => [МУМНОЖ];
5. Умножить исходную матрицу на Y (X’·X)-1·X’·Y => [МУМНОЖ]
Матричный метод МНК.
Понятие статистической процедуры оценивания параметров эконометрической модели. Требования к наилучшей статистической процедуре: несмещённость и минимальные дисперсии оценок параметров.
Оценкой ân параметра a называют всякую функцию результатов наблюдений над случайной величиной X (иначе — статистику), с помощью которой судят о значениях параметра a.
Статистические проверки параметров регрессии основаны на непроверяемых предпосылках распределения случайной величины. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям: быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.
|
|
|
В отличие от параметра, его оценка ã n — величина случайная. «Наилучшая оценка» ã n должна обладать наименьшим рассеянием относительно оцениваемого параметра a, например, наименьшей величиной математического ожидания квадрата отклонения оценки от оцениваемого параметра М(ã - a)2.
Оценка â n параметра a называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. М(ã) = a.
В противном случае оценка называется смещенной.
Если это равенство не выполняется, то оценка ã , полученная по разным выборкам, будет в среднем либо завышать значение a (если М(ã) > a , либо занижать его (если М(ã) < 0). Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
Оценка â n параметра a называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:
|
|
|
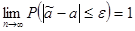
В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки.
Несмещенная оценка ã n параметра a называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра a, вычисленных по выборкам одного и того же объема n.
Так как для несмещенной оценки M(ã n - a)2 есть ее дисперсия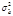 
, то эффективность является решающим свойством, определяющим качество оценки.
Для нахождения оценок параметров (характеристик) генеральной совокупности используется ряд методов.
Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания.
Дата добавления: 2018-08-06; просмотров: 2017; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!