Приведение формулы Букингэма к критериальному виду.
Численное решение уравнения (4.21) можно быстро выполнить только при наличии ЭВМ или, по меньшей мере, программируемых микрокалькуляторов. Гродде предложил оригинальный метод решения уравнения Букингэма с привлечением вспомогательного графика.
Обозначим po/p через  b и разделим обе части уравнения (4.20) на Q :
b и разделим обе части уравнения (4.20) на Q :

Это выражение можно представить и так:
 .
.
Умножим и разделим правую часть на po:
 .
.
Если выразить Q через v и сечение канала трубы, перейти oт R к диаметру d, а также выразить po по формуле (4.6), то получим выражение:
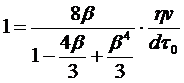 .
.
Разделим обе части на (ηv/τd):
 .
.
Правая часть не имеет размерности, так как b - относительная величина. Следовательно, и левая часть - величина безразмерная и известна под названием "критерий Сен-Венана - Ильюшина":
 . (4.22)
. (4.22)
В результате получаем:
 . (4.23)
. (4.23)
Функцию b = f(Sen) по этому уравнению Гродде представил в виде графика в полулогарифмических координатах. Порядок вычислений при этом следующий. Вначале вычисляют для рассматриваемого случая Sen по формуле (4.22). Затем по специальному вспомогательному графику функции (4.23) находят величину b. Искомую величину потерь давления р определяют из соотношения
 . (4.24)
. (4.24)
Упомянутый график функции b = f(Sen) можно найти в книге: Е. Г. Леонов, В. И. Исаев. Гидроаэромеханика в бурении. - М.: Недра, 1987. - С. 72.
Методика расчета потерь давления при ламинарном режиме движения вязкопластичных и вязких жидкостей в трубах.
Анализ уравнения Букингэма. Формула Бингама.
При po=0 уравнение (4.20) превращается в известную формулу Пуазейля-Гагена. При ро/р=0,5 третий член уравнения
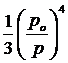
равен 0,0208. Это означает, что его роль едва превышает 2%. Очевидно, при p > 2po третьим членом уравнения Букингэма можно пренебречь и представить его в "усеченном" виде:
 . (5.1)
. (5.1)
Заменим ро на выражение (4.6):
 .
.
Выразим р через другие параметры:
 .
.
Заменим R на диаметр канала труб d:
 . (5.2)
. (5.2)
Эта формула носит имя Бингама.
Если вместо Q пользоваться средней скоростью v, то получим вариант формулы Бингама:
 , (5.3)
, (5.3)
где первый член формулы подставляет собой формулу Пуазейля-Гагена.
Точность формул (5.2) и (5.3), а, следовательно, их применимость, как указано выше, полностью зависит от величины соотношения ро/р.
В табл. 5.1 приведены результаты расчетов по точной (с использованием метода Гродде) и приближенной формулам для случая структурного режима течения в трубах. Анализируя изменение b и р, можно заметить, что:
- на всем диапазоне изменения расхода (от малых значений до критических) величина b не опускается ниже 0,55, причем с увеличением tо минимально достижимое значение возрастает; это означает, что на практике очень редки случаи, когда b £ 0,5;
- погрешность формулы Бингама всегда имеет положительный знак; это означает, что формула Бингама дает всегда завышенный результат (от 3...5 до 18…22%);
- то обстоятельство, что с приближением Q к нулю возрастает уровень завышенности результата расчета, создает с технологической точки зрения некоторый "запас прочности" в расчетах и в некоторой степени как бы учитывает влияние нестационарности в реологическом поведении жидкостей в скважине.
Всё сказанное позволяет уверенно рекомендовать формулу Бингама для использования в практических расчетах, особенно при отсутствии программ для ЭВМ.
Таблица 5.1.
Расчетные значения потерь давления при структурном режиме движения вязкопластичной жидкости по трубе с внутренним диаметром 0,107 м и длиной 1000 м
| Реологические параметры | Расход жидкости, м3/с | Точное решение | Приближенное решение Бингама | Погрешность, % | |
| b | р, Па | р*, Па | |||
| t0 = 4Па h =0,02 Па*с | 0,001 0,002 0,004 0,006 0,013* | 0,860 0,0805 0,730 0,675 0,550 | 173875 185870 204839 221530 271878 | 205594 211810 224243 236677 280193 | 18,24 13,96 9,47 6,84 3,06 |
| tо =8 Па h =0,02 Па*с | 0,001 0,002 0,006 0,0183 | 0,900 0,860 0,764 0,6105 | 332295 347751 391447 489870 | 404971 411187 436064 512518 | 21,87 18,24 11,40 4,62 |
*) Расход, равный критическому, при котором структурный режим течения переходит в турбулентный.
Дата добавления: 2018-06-27; просмотров: 487; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

