Гидравлические сопротивления при движении буровых промывочных жидкостей в скважине.
Напомним, что в задаче о движении жидкостей по трубопроводу различают два вида сопротивлений: линейные и местные. Первые при всех прочих равных условиях пропорциональны длине трубопровода, а вторые отличаются тем, что приурочены к определенному месту и зависят от геометрических особенностей канала в этом месте. Сказанное является справедливым и для циркуляционной системы скважины (рис. 3.6).
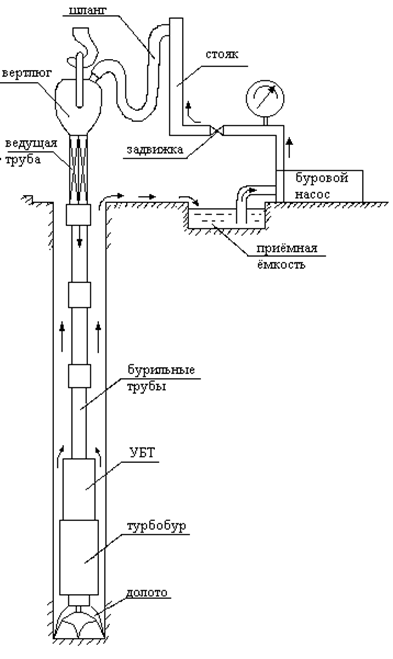
Рис. 3.6. Циркуляционная система скважины.
В колонне труб, спущенных в скважину, можно выделить участки с постоянным живым сечением, например, участки равнопроходного сечения между соединениями труб. Гидравлические сопротивления на таких участках, ecтественно, являются типично линейными. Сопротивления в заколонном пространстве на участках между соединениями также являются по своей природе линейными, пропорциональными длине труб. Что касается мест соединений, то они являются источниками местных сопротивлений.
Итак, для скважины:
pн = Spл + Spм
где pл - линейные сопротивления,
pм - местные сопротивления.
Приведенная формула справедлива для случая, когда все сопротивления располагаются последовательно, друг за другом.
Рассмотрим типичный вариант колонны для турбинного бурения (рис.3.6).
Двигаясь вместе с жидкостью, мы встречаем следующие гидравлические сопротивления:
1) в наземной обвязке буровых насосов (манифольде) на участке от насоса до бурового шланга, которые состоят из местных сопротивлений при прохождении задвижек и линейных сопротивлений по трубам обвязки, а также местных сопротивлении на соединениях труб с буровым шлангом, на изгибах (коленах) труб манифольда;
|
|
|
2) в буровом шланге, где преобладают линейные сопротивления;
3) в вертлюге, где имеют место преимущественно местныесопротивления (повороты, сужения потока, участки с резким его расширением),
4) 
в ведущей трубе (рабочей трубе) - и линейные и местные (в замках);
5) в бурильных и утяжеленных бурильных трубах - линейные (между соединениями труб) и местные - в соединениях;
6) в турбобуре, где перепад давления складывается из перепада давления на лопатках турбины и местных потерь деления всоединенияхмежду секциями турбобура;
7) в промывочных отверстиях долот - это типичные местные сопротивления;
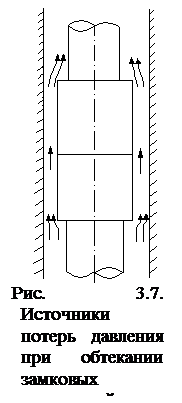
8) в кольцевом пространстве, где сопротивления представлены набором линейных сопротивлений и местных, связанных с наличием резких сужений и резких расширений потока при прохождении замковых (муфтовых) соединений и каверн в скважине; на каждом замковом соединении (рис. 3.7) мы наблюдем три разновидности: линейное сопротивление рмл, местное на входе в узкую часть кольцевого пространства рмси местное сопротивление на выходе из узкой части рмр (потери при резком расширении); влиянием каверн на потери давления обычно пренебрегают.
|
|
|
Подчеркнем ещё раз, что давление на насосах (насосе) определяется как сумма всех давлений pi , затраченных напреодоление всехупомянутых нами сопротивлений.
4. Уравнение расхода для структурного режима движения вязкопластичной
жидкости в круглой трубе.
Уравнения скорости потока жидкости в круглой трубе.
Основное уравнение равномерного движения.
Равномерное движение - основная разновидность движения буровой промывочной жидкости в круглых трубах (бурильных, обсадных или насосно-компрессорных). Дело в том, что подача насосов, как правило, постоянна, а сечение труб по их длинетоже не может меняться (заисключением соединений труб).
Рассмотрим состояние динамического равновесия цилиндрического объёма жидкости, двигающегося равномерно по трубе под действием перепада давления р=р1–р2 (рис. 4.1). Сила внешняя, поддерживающая движение жидкого цилиндра длиной l и радиусом у, равна py2r.Сила сопротивления сосредоточена на внешней поверхности цилиндра и является результатом возникновения касательных напряжений из-за разницы скоростей движения различных слоев на радиусе y. Величина этой силы равна произведению поверхности цилиндра на его длину: 2pylt.
|
|
|
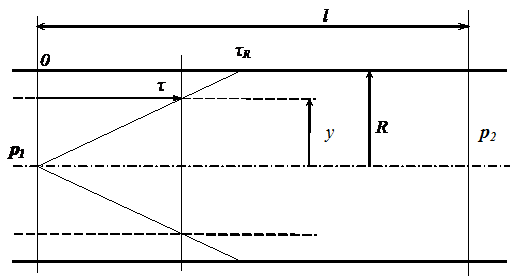
Рис. 4.1. Эпюра напряжений в круглой трубе.
При равномерном движенииобе силы равны:
py2p = 2pylt,
yp = 2lt,
p = 2pylt . (4.1)
При y = R (на стенке трубы) t =tR. Тогда
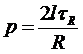. (4.2)
Из уравнения (2.1.) следует,что
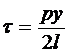. (4.3)
При y = 0 t = 0, а при y = R t = tR. Из формулы (4.3.) следует, что зависимость касательных напряжении от расстояния y имеет линейный характер, причем, на самой оси напряжение равно нулю. Эпюра напряжений для круглых труб показана на рис. 4.1. Из неё видно, что справедливо соотношение
.
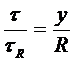Следовательно,
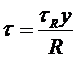(4.4)
или
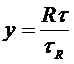. (4.5.)
Если бы существовали методы определения tR (касательных напряжений на стенке трубы), то по формуле (4.2) можно было бы вычислить линейные потери давления при ламинарном движении любой жидкости в круглых трубах. К сожалению, такое невозможно, что вынуждает нас продолжить поиск расчетной формулы.
|
|
|
Дата добавления: 2018-06-27; просмотров: 1389; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!