Вывод уравнения профиля скоростей для случая движения вязкопластичной жидкости в круглой трубе при структурном режиме движения.

Подставим в уравнение (4.10) реологическую функцию (4.9):

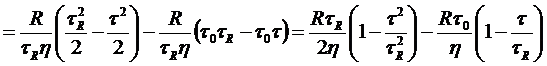Чтобы избавиться от t_R , вспомним уравнение (4.2), из которого следует:

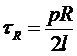. (4.11)

Подставим (4.11) в последний результат и одновременно заменим t /t_R на y/R в соответствии с (4.4):

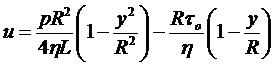Окончательно:

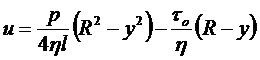. (4.12)

Ранее было показано (см. раздел 4.1.2), что при y = r_o u = u_o , где u_o скорость движения "твердого" структурного ядра. Следовательно,

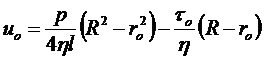. (4.13)

Выразим p в последнем уравнении через остальные:

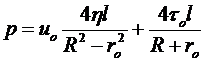. (4.14)

На первый взгляд может показаться, что искомая формула для определения линейных потерь давления p для случая структурного движения ВПЖ в трубах найдена. Но это не так. Дело в том, что измерить или каким-то косвенным методом вычислить u_o , r_o практически невозможно. Формула (2.14) не имеет практического значения, но имеют конкретное значение уравнения (4.12) и (4.13), в чем мы убедимся, если познакомимся с материалом следующего подраздела.

Формула Букингэма (уравнение расхода вязкопластичной жидкости).

Вывод формулы Букингэма.

Нашей целью является получение такой формулы для определения p , в которой использовались бы параметры, нахождение которых не вызывало бы затруднений. Вместо переменной скорости u по сечению предпочтительнее пользоваться средней скоростью v или расходом Q.

Вместо неопределенного радиуса r_о лучше иметь дело с радиусом трубы R или диаметром d.

Расход потока ВПЖ при структурном режиме Q можно определить, если просуммировать (проинтегрировать) расходы элементарных кольцевых струек с толщиной dy по всему сечению потока (рис. 4. 4). В градиентном слое расход струйки dQ_Г выражается уравнением

dQ_Г = 2pydyu .                                     (4.15)

В ядре

dQ_o = 2pydyu_o .                                    (4.16)

Тогда общий расход Q:

.

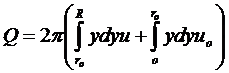Заменим u и u_o на их выражения из формул (2.12) и (2.13):

.

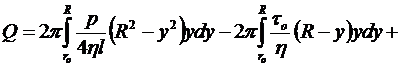
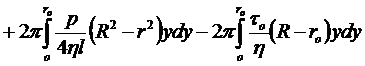Интегрирование этого выражения дает результат:

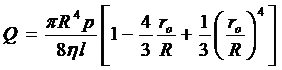.                  (4.17)

Докажем, что r_o/R   можно заменить на p_o/p, где p_o - начальное давление, определяемое по формуле (4.6):

.

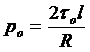Из условия динамического равновесия движущегося структурного ядра следует, что

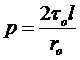.                                             (4.18)

Отсюда:

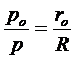.                                              (4.19)

В результате уравнение (4.17) приобретает вид, вполне пригодный для выполнения практических расчетов:

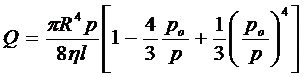.                  (4.20)

Это уравнение носит имя Букингэма, и было получено им в 1921 году.

Вэтом уравнении искомая величина потерь давления p не может быть в явном виде выражена через другие. Если задаваться расходом Q и другими параметрами (l, R, h, t_o ), то величину p можно вычислить численным методом. В уравнении (4.20) величина p_o   определяется предварительно по формуле (4.6). Если подставить (4.6) в уравнение (4.20), то получим:

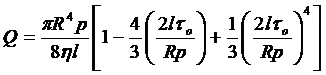.            (4.21)

Решение, полученное Букингэмом, называют точным. Но при этом следует добавить: при условии, что реологическое уравнение полностью соответствует уравнению

.

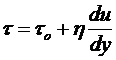Это значит, что при изменении du/dy от нуля до любых действительных значений в пределах структурного и ламинарного движения реограмма не должна отклоняться от прямой, что, как было ранее показано, не всегда бывает, например, в модели Шведова (с начальным криволинейным участком).

Отношение p_o /p близко к единице при Q, близких к нулю. При расходах, характерных для процесса бурения скважины (как при роторном, так и турбинном бурении), p_o/p может существенно отличаться от 1 и приближаться к 0,5.

Дата добавления: 2018-06-27; просмотров: 622; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!