Приведение уравнения Бингама к критериальному виду.

⇐ ПредыдущаяСтр 11 из 26Следующая ⇒

В практических руководствах по гидравлическим расчетам в бурении очень часто при любых режимах течения рекомендуется пользоваться формулой Дарси-Вейсбаха. Такой традиционный подход сохраняется и для структурного режима течения ВПЖ в трубах круглого сечения, хотя было показано, в предыдущем подразделе, цель достигается проще при использовании формулы Бингама.

В такой целевой постановке задача сводится к выводу формулы для коэффициента гидравлических сопротивлении l.

Возьмем формулу Бингама в форме (5.3):

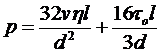Очевидно, результат расчета по этой формуле должен численно совпасть с результатом расчета по формуле Дарси-Вейсбаха:

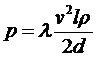. (5.4)

Если правые части уравнений равны, то

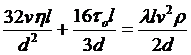Выразим l из этого уравнения:

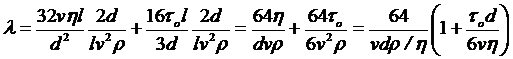Выражение в знаменателе

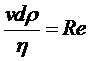Как нам уже известно,

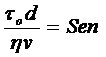Следовательно,

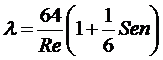. (5.5)

Напрашивается аналогия этой формулы с известной формулой

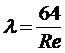Формулу (5.5) можно преобразовать к традиционной, если ввести обозначение

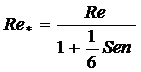. (5.6)

Тогда можно утверждать, что формула Дарси-Вейсбаха даст точно тот же результат, что и формула Бингама, если

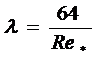. (5.7)

5.3. Расчёт линейных потерь давления при ламинарном
движении вязких жидкостей в трубах.

При промывке скважины водой существование ламинарного режима в любoм из элементов циркуляционной системы практически невозможно, если иметь в виду реальные расходы Q. Вместе с тем применение вязких нефтей при освоении скважин или специальных жидкостей, например, при цементировании, делает существование ламинарного режима движения в трубах вполне возможным.

Если в уравнение (4.10) подставить реологическую функцию φ(τ)=τ/η, то получится решение:

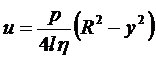. (5.8)

Подставив это уравнение в выражение (2.15) и проинтегрировав его в пределах изменения y от 0 до R , получим известное решение Пуазейля-Гагена

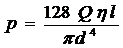(5.9)

или, выразив расход через среднюю скорость, формулу

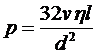. (5.10)

Решение будет таким же, если воспользоваться формулой Дарси-Вейсбаха:

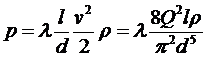, (5.11)

где

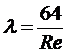. (5.12)

Иначе говоря, формулы (5.11) и (5.12) являются критериальной формой решения Пуазейля-Гагена, пригодной для определения потерь давления в круглой трубе при течении вязкой жидкости в ламинарном режиме.

Комментарий к разделам 4 и 5.

Обращаю внимание уважаемого студента (или читателя) на то, каким образом (в какой логической последовательности) были получены формулы для расчета линейных потерь давления в трубах при структурном режиме движения.

Сначала (раздел 4.1.1) было установлено, что при равномерном движении жидкостей в трубах внутренние касательные напряжения меняются линейно в зависимости от расстояния oт оси трубы, причем на самой оси напряжение равно нулю. Попутно было доказано существование структурного ядра потока (раздел 4.1.2).

Надо заметить, что линейная зависимость напряжения от радиуса - это особенность только круглой трубы.

Стало очевидным, что одним и тем же потерям (в одной и той жетрубе с известной длиной) соответствует одна и та же эпюра напряжений, которая "устанавливается" как бы автоматически, независимо от жидкости. Достаточно, чтобы при этом режим движения был ламинарным или структурным. Становится ясным, что жидкость так "приспосабливается" к эпюре напряжений, создает такую эпюру скоростей в трубе, чтобы градиенты скоростей по радиусу автоматически "воссоздавали" линейный характер зависимости касательных напряжении (между слоями потока) от расстояния от оси грубы.

Представим теперь, что две разные жидкости, одна из которых вязкая (ньютоновская), а другая - вязкопластичная, двигаясь по одной и той же трубе, вызывают одни и те же потери давления р. Режим движения, предположим, при этом соответственно ламинарный и структурный. Первая жидкость "образует" эпюру скоростей по сечению в виде параболы, параметры которой будут точно соответствовать эпюре напряжений по уравнению τ =py/(2l). Вторая жидкость (вязкопластичная) тоже "сформирует" свою эпюру (теперь мы уже знаем, что она будет состоять из структурного ядра, двигающегося со скоростью u_o и градиентного слоя, где скорость меняется от до u_o по закону, близкому к параболическому). Но, что особенно важно подчеркнуть, эпюра напряжений, несмотря на различие в эпюрах скоростей, будет та же, что и в первом случае, поскольку перепад давления p тот же самый (те же потери давления). Различие в эпюрах скоростей при идентичности эпюры напряжении является следствием различия в реологической модели. Влияние модели жидкости на эпюру скоростей было рассмотрено (для общего случая) в разделе 4.1.3.

Полученное в этом разделе уравнение (4.10) было решено в разделе 4.1.4 для конкретного случая вязкопластичной жидкости. В результате были получены уравнения (4.12) и (4.13), описывающие эпюру скоростей в круглой трубе.

Наконец, в разделе 4.2, основываясь на полученных уравнениях (4.12) и (4.13), методом суммирования (интегрирования) расходов элементарных кольцевых струек в трубе (при известной теперь уже эпюре скоростей) получено уравнение расхода, носящее имя Букингэма. Предложены методы решения этого уравнения и исследованы возможности упрощения уравнения (формула Бингама).

Итак, базируясь на линейном характере эпюры напряжений и выбирая конкретную реологическую модель жидкости, сугубо аналитически получены расчетные формулы для определения линейных потерь давления в трубах при структурном режиме движения вязкопластичной жидкости, соответствующей бингамовской реологической модели. Теперь смело можно утверждать, что мы умеем вычислять потери давления на внутреннее трение при напорном движении вязкопластичной жидкости в круглой трубе, если оно происходит при структурном режиме.

6. Турбулентный режим движениявязких и вязкопластичных
жидкостей в трубах.

6.1. Кризис структурного режима движения в трубах.
Определение критических скорости и расхода.

В отличие от вязких (ньютоновских) жидкостей, которые "входят" в турбулентный режим при достижении одного и то же критического числа Re, равного 2320, вязкопластичные жидкости такого единственного и универсального числа Re не имеют. Более того, как показали эксперименты, кризис структурного режима с последующим переходом в турбулентный режим может начаться при различных значениях Re_кр в зависимости от конкретных значений величин t_о, h, d и r.

После обработки многочисленного экспериментального материала Е.М. Соловьев получил формулу для Re_кр :

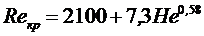, (6.1)

где

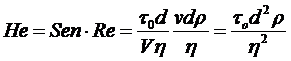(6.2)

называется числом (критерием) Хёдстрема.

Зная Re_кр , нетрудно найти v_кр и Q_кр:

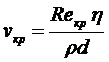, (6.3)

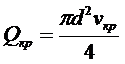, (6.4)

При τ_o > 5 Па можно воспользоваться менее точной формулой, впервые предложенной Б.С. Филатовым:

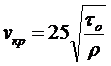. (6.5)

Таким образом, предлагаются две методики прогнозирования начала турбулентного движения.

Предпочтение следует отдавать, разумеется, более строгой методике Е.М. Соловьева.

Полезно заметить, что Не есть величина, не зависящая oт скорости или расхода, а только от диаметра трубы и параметров жидкости. Это обстоятельство делает формулу (6.1) более универсальной.

6.2. Профиль скоростей при турбулентном режиме движения
в трубах и его роль при замещении одной жидкости другой.

Турбулентное движение неньютоновских жидкостей в трубах изучено слабо, поэтому будем придерживаться рабочей гипотезы о сходстве между турбулентными потоками вязкой и вязкопластичной жидкостей.

Экспериментальное и теоретические исследования (полуэмпирические теории Прандтля или Альтшуля) показывают, что в переходной области (до достижения квадратичной области движения, которую иногда называют вполне шероховатым течением или автомодельным, не зависящим от Re) профиль скорости явно зависит от числа Re. Считается, что профиль скорости может быть описан степенным уравнением (аппроксимация более строгого решения):

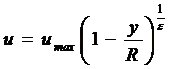, (6.6)

где u_max - максимальная скорость в центре потока (рис. 6.1);

u – скорость на радиусе у;

ε – величина, зависящая от Re, изменяется в пределах от 6 до 10.

При Re<10⁵ величину ε можно принять равной 7 (отсюда выражение "закон одной седьмой").

На рис. 6.1показаны типичные эпюры скоростей, возникающих при движении бурового раствора в нефтепромысловых трубах.

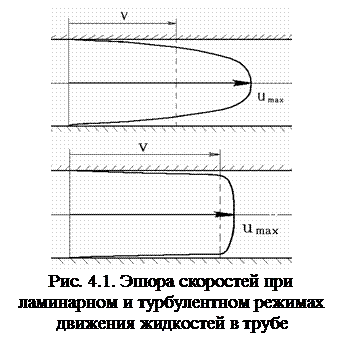При промывке скважины вязкими жидкостями в ламинарной области или вязкопластичными жидкостями при расходах, близких к Q_кр , возникает представляющая собой параболу. Этот вариант движения крайне невыгоден при замещении в трубах одной жидкости другой, поскольку центральная часть вытесняющего потека сильно отличается от скоростей у стенки труб и "внедряется" в вытесняемый поток. В результате с течением времени создается зона смешения с переменной концентрацией вытесняющей жидкости по длине зоны. В сравнении с ламинарным движением турбулентный режим выглядит более предпочтительным, так как обеспечивает несравненно более выравненную эпюру скоростей по радиусу трубы , соответствующую формуле (6.6). Только у стенки трубы наблюдается резкое уменьшение скорости u. Следовательно, при турбулентном движении достигается хорошее вытеснение с минимальной длиной зоны смешения. С течением времени длина зоны смещения будет нарастать кратно медленнее, чем в предыдущем случае. Иначе говоря, если есть реальная возможность с помощью насосов поддерживать расход Q, превышающий Q_кр, то следует процесс замещения проводить при турбулентном режиме, а не при ламинарном.

К сожалению, при строительстве скважины далеко не всегда имеется техническая и технологическая возможность "добраться" до турбулентного режима. Например, при цементировании обсадных колонн диметром 245, 324 или 426 мм, как правило, не только на стадии затворения цементного раствора, но и при его продавке, невозможно обеспечить подачу насосов с превышением критических расходов для трубного и - тем более - затрубного пространства. В подобных ситуациях необходимо перейти на так называемый "пробковый" режим с эпюрой скоростей типа 1 на рис. 4.3. Необходимо уменьшить расход Q до величин, при которых радиус структурного ядра r_о будет, по возможности, больше. Чрезмерное уменьшение Q затянет время цементирования колонны, но увеличение Q , как было показано в разделе 4.1.2, уменьшает радиус ядра. Для улучшения условий замещения жидкости необходимо увеличивать радиус ядра, иначе говоря, уменьшать Q. С другой стороны, увеличить r_о можно некоторым увеличением структурной прочности жидкости.

6.3. Расчет линейных потерь давления при турбулентном
режиме движения в трубах.

В случае вязких жидкостей рекомендуется воспользоваться решением А.Д. Альтшуля, который предложил формулу для коэффициента гидравлических сопротивлений l:

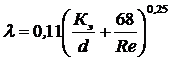, (6.7)

где К_э - эквивалентная шероховатость.

Эта формула справедлива как в переходной, так и в квадратичной области, поскольку при больших Re она практически превращается в формулу Шифринсона (ввиду малости второго слагаемого в скобках):

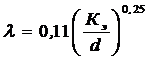. (6.8)

Лабораторные и натурные исследования показали, что при турбулентном движении вязкопластичных жидкостей в трубах потери давления определяются по формуле Дарси-Вейсбаха, при этом сначала вычисляют Sen по формуле (4.22), затем Re и Re_* по формуле (5.6), а коэффициент l - по формуле:

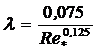. (6.9)

Формула рекомендуется для интервала изменения Re_* от 4000 до 50000.

Если Re_* > 50000, то для практических расчетов l можно считать постоянным и равным 0,02.

7. Линейные потери давления при движении псевдопластичной ("степенной") жидкости в трубах.

Дата добавления: 2018-06-27; просмотров: 549; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Мы поможем в написании ваших работ!