Распределение скоростей по сечению потока.

Речь идет о закономерности распределения скорости вдоль радиуса трубы, в сечении, проведенным перпендикулярно потоку.

В осесимметричных каналах распределение скоростей можно изобразить эпюрой скоростей. В центре потока скорость u_o максимальна, а на границе со стенками (вследствие гидрофильности жидкости) скорость равна нулю. Эпюра скоростей при ламинарном течении вязкой жидкости (pиc. 3.1) существенно отличается от таковой при турбулентном движении (рис. 3.2).

Рис. 3.1. Эпюра скоростей при ламинарном движении вязкой жидкости.

Рис. 3.2. Эпюра скоростей при турбулентном движении вязкой жидкости.

Средняя скорость потока v.

В расчетной практике удобнее иметь дело не со скоростями, переменными по сечении (эпюрой скоростей), а со средней по сечению скоростью. Нетрудно догадаться, что средняя скорость v равна длине образующей цилиндра, объем которого равен объему тела вращения, образованного эпюрой скоростей.

Чтобы измерить среднюю скорость потока, необходимо объем жидкости, прошедшей через данное сечение в единицу времени, Q разделить на площадь поперечного сечения потока (основания пространственной эпюры скоростей) f:

v = Q / f . (3.2)

Уравнение неразрывности. Если жидкость движется по трубопроводу сплошным потоком, без образования разрывов и пустот, то для такого потока всегда справедливо условие

Q = const. (3.3)

Это, в частности, означает, что v обратно пропорционально сечению, или

v_i f_i = const (3.4)

Напорное и безнапорное течение. Если жидкость, двигаясь по трубе, заполняет все сечение, то такое течение называют напорным.

При безнапорном (русловом) течении сечение потока меньше сечения трубы. В бурении такое течение наблюдается в желобах.

Смоченный периметр χ. Это та часть периметра живого сечения, по которой происходит соприкосновение жидкости с ограничивающими её стенками.

Для случая, показанного на рис. 3.3:

χ = pD,

Для варианта, изображенного на рис. 3.4:

χ = 2h + в,

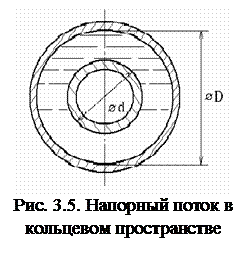
Для кольцевого канала (рис. 3.5):

χ = p(D+d).

Гидравлический радиус. Отношение живого сечения потока к смоченному периметру χ называется гидравлическим радиусом R_Г:

. (3.5.)

Дляслучая на рис. 3.3:

. (3.6)

Для кольцевого канала (рис. 3.5):

. (3.7)

Понятие о гидравлическом радиусе широко используется в гидравлике буровых растворов.

Из сравнения формул (3.6) и (3.7) следует, что условием совпадения гидравлических радиусов труб и кольцевого пространства является равенство:

d_в = D – d_н.

Рассмотрим теперь циркуляционную систему скважины. В сущности, это трубопровод, но только составленный из каналов различной геометрической формы. Вначале жидкость движется вниз по трубам, а поднимается вверх по каналу, образованному двумя трубами – по кольцевому (заколонному) пространству. Жидкость возвращается туда, откуда начала своё движение (см. рис. 3.6).

Составим уравнение Бернулли для потока, ограниченного начальным сечением 1-l, проведенном на уровне начального сечения манифольда и конечным сечением 2-2 заколонного пространства на устье скважины:

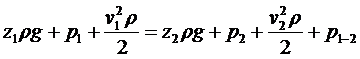, (3.8)

где p_1-2 - потери давления, затрачиваемые на поддержание движения на участке между сечениями 1 - 1 и 2 - 2.

По условию z₁=z₂, а p₂= 0 , поскольку выходящий из скважины поток изливается в желоб, где давление равно атмосферному.

Давление p₁ - это деление на насосах при промывкеp_н.Следовательно, p₁=p_н.

Гидродинамическими составляющими v₁²/r и v₂²/r можно пренебречь ввиду их малости по сравнению с p_н.

В результате уравнение Бернулли превратится в равенство

p_н = p_1-2 . (3.9)

Это означает, что давление на буровых насосах при промывке скважины численно равно потерям давления в циркуляционной системе от насоса до устья скважины.

Получается, что для определения ожидаемого давления на насосах достаточно вычислить и просуммировать все потери давления в скважине, Сказанное справедливо только в том случае, когда плотность бурового раствора на всех участках циркуляционной системы одна и та же.

Дата добавления: 2018-06-27; просмотров: 1824; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!