Уравнения гидростатики буровых жидкостей.

Дифференциальное уравнение гидростатики.

Выделим внутри покоящейся жидкости (рис. 1.1) параллелепипед с ребрами, расположенными параллельно координатным осям Ох, Оу и Oz равным соответственно dx, dy, dz. Составим уравнение равновесия этого параллелепипеда.                                                               

Рис. 1.1. К выводу основного дифференциального уравнения гидростатики.

 

Условия равновесия: проекция всех сил (поверхностных и массовых) на оси координат поочередно равны нулю.

dP=p∙dy∙dz и dP'=p'∙dy∙dz,

где р и р' – гидростатические давления на элементарных площадках ABCD и A'B'C'D'; Р и Р' – силы, действующие на эти площадки.

Основываясь на тезисе о непрерывности и однородности среды, принимаем, что гидростатическое давление является непрерывной функцией координат.

Это означает, в частности, что справедливо уравнение:

,

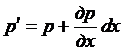поскольку при переходе от площадки ABCD к площадке A'B'C'D' по направлению оси Ох меняется только координата х. Тогда

.

В параллелепипеде заключена масса жидкости dm=ρ∙dx∙dy∙dz, на которую в общем случае может действовать сила . Здесь  – вектор, результирующей массовой силы, а 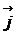 – вектор ускорения, полученный в результате действия этой силы. Проекция силы на ось будет равна:

F_x=dm∙j_x=ρ∙dx∙dy∙dz∙j_x.

Условие равновесия тогда запишется уравнением:

Р – Р^'+F_x=0;

;

;

.

Аналогично можно получить уравнение равновесия по проекциям сил на оси Оу и Oz. В результате получим систему уравнений:

;

;

.

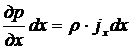Сложим левые и правые части:

.

Левая часть уравнения – это полный дифференциал функции. В результате:

dp=ρ(j_xdx+ j_ydy+ j_zdz ).                                  (1.1)

Это уравнение называется основным дифференциальным уравнением гидростатики.

Основные уравнения гидростатики.

Рассмотрим несколько частных случаев решения полученного уравнения применительно к задачам буровой гидравлики.

Поместим в скважину, заполненную вязкой жидкостью (например, глинистым раствором) так, как показано на рис. 1.2. Ось скважины направлена вертикально и параллельно оси Oz. Ось Ох направим, следовательно, горизонтально.

Жидкость в точке М в герметичной скважине с координатой z будет находиться в покое в поле земного тяготения. При выбранных нами направлениях координатных осей массовая сила – сила веса будет направлена вдоль оси Оz. Следовательно, проекции массовой силы на другие оси будут равны нулю. Это значит, что в уравнении (1.1) j_x и j_y соответственно будут равны нулю, а j_z= – g.

dp=-ρgdz.

Знак "-" появляется от того, что направление оси Oz не совпадает с направлением силы тяжести.

Проинтегрируем, помня о том, что для жидкости ρ=const:

dp+ρgdz=0,

.

Это означает, что в общем случае

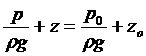,                                 (1.2)

где р_o и z_o – известное давление в точке с заданной координатой z­_o.

Рис. 1.2. К выводу основного уравнения гидростатики.

 

Решение (1.2) называется основным уравнением гидростатики, которое чаще представляют в виде:

р=р_o+ρg(z_o-z )                                           (1.3)

или

р=р_o+ρgh,                                               (1.4)

где h – глубина погружения под уровень жидкости, где давление известно.

В скважине, в отличии от многих гидротехнических задач, не всегда р_o и z_o – это соответственно давление и координата свободной поверхности, где давление равно атмосферному. В закрытой, но герметичной скважине р_o и z_o – могут быть информацией на любой глубине. Нередко приходится определять давление жидкости на меньшей глубине, пользуясь данными о давлении на значительно большей глубине. Поэтому при решении задач по гидростатике буровой жидкости лучше пользоваться либо уравнением (1.2), либо понятием о положительной (z_o<z) и отрицательной (z_o>z) глубине.

Примечание: при использовании уравнения (1.2) надо всегда помнить, что при его выводе ось Oz не совпадала по направлению с направлением силы тяжести.

Уравнение (1.4) – это уравнение прямой. Это значит, изменение давления в скважине зависит только от глубины при ρ=const, независимо от того, открытая скважина или находится под давлением.

Рис. 1.3. Изменение гидростатического давления с глубиной в открытой скважине.

 

 

На рис. 1.3 показана эпюра (график) давлений в открытой скважине, а на рис. 1.4 – в закрытой с избыточным давлением р_у на устье скважины. В последнем случае давление на любой глубине l (в буровой литературе вместо h обычнопишут l):

р=р_у+ρgl,                                                (1.5)

так как р_o=р_у, а h=l.

 

Рис. 1.4. Изменение давления с глубиной в скважине
с избыточным давлением на устье.

 

 

Рис. 1.5. Эпюра давления при проявлении из скважины.

 

 

Еще один пример. Найти давление на устье скважины, если известны пластовое давление р_пл и глубина проявляющего пласта l_пл (рис. 1.5). Из рисунка видно, что в данном случае l_пл – величина отрицательная, так как известно давление на большей глубине, а необходимо найти давление на устье скважины.

Рис. 1.6. Эпюра давлений при частичном замещении бурового раствора в скважине нефтью.

 

Следовательно,

р=р_пл,     l=l_пл,

а искомое давление р_у:

р_у=р_пл – ρgl_пл.                                          (1.6)

Несколько усложним задачу. Представим себе, что в проявляющей скважине (при избыточном давлении на устье) находятся две жидкости – нефть и буровой раствор – соответственно с плотностью ρ_н и ρ_р причем высота столба их в скважине равна соответственно h_н­ и  h_р. Нетрудно доказать, что в данном случае устьевое давление определяется по формуле:

р_у=р_пл–(ρ_н∙g∙h_н+ρ_р∙g∙h_р).                                     (1.7)

Эпюра давлений в скважине показана на рис.1.6.

---

Дата добавления: 2018-06-27; просмотров: 375; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!