Давление на стенки наклонно направленной скважины.

⇐ ПредыдущаяСтр 5 из 26Следующая ⇒

Наклонно направленная скважина, которая заполнена жидкостью, находящейся в покое в поле земного тяготения, показана на рис. 2.5.

Когда массовые внешние силы представлены только силами тяжести, к жидкости, независимо от ее вида (вязкая или ВПЖ), можно применить основное уравнение гидростатики, в котором, как хорошо известно, нет координат x и y. Для точек (уровней) z_о и z (в точке М) это уравнение запишется в виде:

или

р=р_о+ρg(z_о-z)=p_о+ρgh_в,

где h_в – погружение точки (уровня) М по вертикали.

Вывод: давление столба жидкости на стенки наклонно направленной скважины зависит только от плотности жидкости и глубины скважины по вертикали. Пространственное положение ствола, следовательно, значения не имеет.

Совсем иное дело, когда решается задача о "пусковых" давлениях на насосах и задача о "сифонах" или опорожнении труб при спуске.

Совершенно очевидно, что величины θ и τ_о не зависят от координат, следовательно, силы сопротивления в жидкости также не зависят от того, вертикальная скважина или наклонная. Нетрудно доказать, что величины р_о и р_ост для наклонно направленной скважины определяются по формулам, аналогичным формулам (2.3) - (2.5), если под l_i и L_к понимать действительные длины секций и колонны в наклонно направленной скважине. Точно так же при расчете высоты подъема жидкости или опорожнения труб при спуске следует воспользоваться формулой (2.8), подставляя вместо L_к фактическую длину колонны L_кн (рис. 2.5).

Вывод: при расчетах пусковых давлений или остаточных давлений на насосах, определении глубины снижения уровня вязко-пластичной жидкости при спуске колонны или высоты подъема жидкости в трубах (подъем с "сифоном") расчеты следует вести, пользуясь фактическими длинами труб по стволу скважины.

Дегазация бурового раствора.

Известно, что для очистки скважины от газа, поступившего в раствор из пласта, используются вакуумные дегазаторы, роль которых сводится к тому, чтобы путем уменьшения давления создать условия для интенсивного всплытия газовых пузырьков из находящейся в покое буровой промывочной жидкости.

Уменьшение давления в дегазаторе сопровождается расширением газовых пузырьков с последующим их всплытием.

Предположим, что в дегазатор поступил газовый пузырек с диаметром d_о.г, стремящийся всплыть под действием архимедовой силы F_а (рис. 2.6), которой противодействуют силы "поверхностные", связанные с наличием структурной прочности жидкости, оцениваемой статическим напряжением сдвига q. В первом приближении пузырек газа можно уподобить шарообразной твердой частице с плотностью, равной нулю. Силы сопротивления среды всплытию F_q будут располагаться на поверхности шара и будут ей пропорциональны. Состояние предельного статического равновесия газа в вязкопластичной жидкости описывается уравнением:

, (2.9)

где ρ - плотность жидкости,

К_ф - коэффициент формы, величина которого для шарообразных тел можно принять равной 2,5.

Следовательно, пузырек газа начнет всплывать при наступлении неравенства:

. (2.10)

С практической точки зрения интересно ответить на два вопроса:

- какого начального диаметра d_а газовые пузырьки могут всплывать в дегазаторе, в котором поддерживается заданный вакуум p_вк и находится жидкость с известными ρ и q;

- какова должна быть величина вакуума, если известны ρ и q и размер пузырьков d_о.г.

Ответ на первый вопрос. Предположим, что при атмосферном давлении p_а из скважины выходит буровой раствор, в котором содержится газ с размерами пузырьков d_а, которые не могут "самостоятельно" всплывать в атмосферных условиях из-за несоблюдение условия (2.10). Попав в дегазатор, где абсолютное давление (р_а – р_вк), газ расширится и, если достигнет размера по формуле (2.10), отделится от жидкости, то есть начнется процесс дегазации.

Расширение газа будет происходить в изотермических условиях, следовательно, по уравнению:

Тогда диаметр пузырьков в дегазаторе можно определится по формуле:

. (2.11)

Всплытие газа в дегазаторе начнется тогда, если левая часть будет больше диаметра, найденного по формуле (2.10). Следовательно, если d_г приравнять к правой части выражения (2.10), то получится формула для определения начального диаметра пузырьков, которые можно удалить из раствора в дегазаторе:

. (2.12)

Если в выходящем из скважины буровом растворе газовые пузырьки будут по диаметру больше, чем рассчитанные по формуле (2.12), то можно быть уверенным, что при вакууме р_вк раствор будет освобожден от газа.

Ответ на второй вопрос. Интересно проанализировать, как зависит потребный для удаления из раствора газовых пузырьков вакуум от их размера. Для этого достаточно в формуле (2.12) выразить р_вк через другие величины:

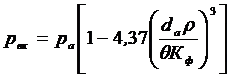. (2.13)

На рис. 2.7 приведены графики зависимостей р_вк=f(d_a) при различных значениях q.

Часть II. Гидродинамика буровых промывочных жидкостей

3. Общие сведения о потоках в циркуляционной системе скважины.

3.1. Основные виды движения. Параметры движения
несжимаемой жидкости.

Под действием внешних сил (сила тяжести, давление насоса и т.п.) жидкость может выйти из состояния покоя и придти в движение.

Различают два основных вида движения: установившееся и неустановившееся.

Неустановившимся движением жидкости называется такое, при котором скорость течения и гидродинамическое давление в каждой данной точке изменяются, иначе говоря, они зависят не только от координат, но и от времени. Примером такого движения является движение жидкости по трубе, присоединенной к емкости, из которой выливается предварительно налитая в неё жидкость. По мере опорожнения емкости скорость жидкости в любой точке трубы будет постоянно уменьшаться.

Другим примером является так называемое "отрывное" течение жидкостей в скважине при закачке цементного раствора в обсадные трубы. Вследствие того, что плотность цементного раствора больше плотности бурового, в процессе закачки наступает момент, когда избыточное гидростатическое давление оказывается больше суммарных гидравлических потерь в системе, и цементный раствор в трубах начинает с некоторым ускорением "убегать" от закачиваемого с постоянной подачей раствора на устье скважины.

Установившимся движением называется такое движение, при котором в данной точке пространства скорость, давление, плотность с течением времени остаются неизменными. Если в первом примере уровень жидкости в емкости поддерживать на одной и той же отметке, то в трубе движение жидкости будет установившимся.

Различают ламинарное (по отношению к вязкопластичным жидкостям часто вместо "ламинарное" говорят "структурное") и турбулентное движение. При ламинарном движении имеет место слоистое, упорядоченное, параллельно-поступательное движения, когда один слой перемещается относительно другого, не перемешиваясь с ним. Такое движение наблюдается при малых скоростях движения,и в случае течения так называемых вязких жидкостей, типичной представительницей которых является вода, хорошо описываемого моделью Ньютона:

. (3.1)

Если теперь постепенно увеличивать скорость движения жидкости воды, то наступает такой момент, когда характер движения резко, почти скачкообразно, изменится. Слоистое упорядоченное движение перейдет в турбулентное, отличающееся неупорядоченным, интенсивно перемешивающимся, хаотичным движением. Впрочем, все это известно из курсов физики и гидравлики. Отметим только, что между ламинарным и турбулентным возможна неустойчивая форма движения, когда одновременно могут существовать две формы, но эта область скоростей весьма ограничена.

Дата добавления: 2018-06-27; просмотров: 402; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!