Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта.

Введем допущения:

- газ не растворяется в жидкости;

- процесс всплытия происходит в изотермических условиях;

- скважина герметична.

Поступивший из пласта некоторый объем газа под действием архимедовой силы, естественно, стремится переместиться вверх по стволу скважины (всплыть). Такой процесс, когда наблюдается движение газа из пласта в скважину и по скважине – к устью называется газопроявлением, которое может стать причиной открытого газового фонтана. В подобных случаях скважину закрывают превентером, после чего все, что находится в скважине оказывается в состоянии покоя и появляется возможность применить законы гидростатики.

Зафиксируем три положения равновесного состояния, когда газовый "пузырь" находится:

- напротив проявляющего газового пласта с пластовым давлением р_пл (рис. 1.7а);

- в середине интервала от пласта до устья скважины (рис. 1.7б);

- на устье (рис. 1.7в).

Объем газового пузыря, поступившего в герметичную скважину, не может ни уменьшаться, ни увеличиваться хотя бы потому, что жидкость принимаем в первом приближении несжимаемой. Следовательно, при движении газа его объем V=const. Если пренебречь влиянием температуры на давление газа (мы договорились, что процесс изотермический) при его движении снизу вверх, то в соответствии с законом Бойля-Мариотта

pV=const,

и давление должно оставаться неизменным, то есть

р=р_пл.

Это означает, что в данной задаче всегда известно давление на границе газа с жидкостью. Следовательно, можно рассмотреть состояние покоя верхней и нижней частей жидкости, применяя основное уравнение гидростатики к указанным частям покоящейся в скважине жидкости с той лишь разницей, что отсчет глубины (отрицательный для верхней части и положительный – для нижней) надо брать от границ раздела жидкости и газа.

Для верхней части давление определяется по формуле:

р=р_пл–ρgl_p, (1.8)

а для нижней –

р=р_пл+ρgl_p, (1.9)

где l_p – расстояние от газа до заданной точки в жидкости.

На рис. 1.7 показано изменение давления в скважине при всплытии газа. Видно, что по мере того, как газовый пузырь, внутри которого давление постоянно и равно р_пл, приближается к устью, давление в скважине растет. Самым опасным является момент, когда газ достигает устья скважины. В этом случае давление во всех точках скважины максимальное. И в результате получается, что простое гравитационное перемещение небольшого газового пузырька, размеры которого несоизмеримы с размерами скважины, создает весьма опасную с точки зрения разрыва колонны внутренним давлением ситуацию. Именно поэтому надо быть очень внимательным, когда при газопроявлениях закрыто устье скважины. Необходимо внимательно следить за давлением на устье р_у, своевременно открывать задвижку ("стравливать" давление), уменьшая тем самым устьевое давление, не допуская, чтобы оно оказалось более допустимого.

Логично задаться вопросом: какое количество газа, поступившего из пласта в скважину, опасно для ведения буровых работ?

Рис. 1.7. Изменение давления в герметичной скважине при всплытии газа, поступившего из вскрытого пласта.

При анализе всплытия газового пузыря в герметично закрытой скважине мы считали жидкость абсолютно несжимаемой. И пришли к выводу, формально правильному, что даже совсем небольшой газовый пузырек может привести к плачевному результату. На деле, разумеется, дело обстоит несколько иначе. Дело в том, что эффект этот может проявиться только там, где величина объемной деформации жидкости под действием давления в газовом пузыре существенно меньше объема газового пузыя, всплывающего по скважине вверх. Известно, что при увеличении давления на 10 МПа объем жидкости уменьшается на 0,5%. Предположим теперь, что из пласта с давлением 30 МПа в скважину поступил газ с глубины 3000 м. Примем, что высота столба газа равна 10 м. Оказавшись на устье, газовый пузырь создает дополнительное давление на жидкость 30 МПа. Под действием такого давления жидкость сожмется на 1,5%, т.е. уровень жидкости в скважине (под газовым пузырем) "просядет" на 45 м, что в 4,5 раза больше объема газа. Очевидно, что такая предоставившаяся газу возможность расшириться приведет к уменьшению давления в газовом пузыре и равновесие наступит при значительно меньших давлениях по сравнению с ожидаемыми, полученными при расчетах без учета сжимаемости жидкости.

Установлено, что описанный выше эффект роста давления до опасных величин на устье и в скважине в целом наблюдается при поступлении газа более 5% от объема скважины, причем неважно, поступает он сразу или постепенно. Именно поэтому нужно быть предельно внимательным со скважинами, находящимися под давлением или находящимися во временной консервации со вскрытым газовым пластом.

Равновесие газов в скважине.

При бурении скважин на различных этапах ее строительства, создаются ситуации, когда скважина (обычно закрытая) заполнена сжатым газом, создающим определенное давление на стенки скважины. Знание величины этого давления необходимо для расчетов обсадных колонн, оценки вероятности гидроразрыва пласта и т.п. Поэтому умение прогнозировать ожидаемые давления при возможных газопроявлениях с полным или частичным замещением жидкости в скважине газом имеет важнейшее значение.

Предположим, что закрытая скважина от кровли газоносного пласта до устья заполнена газом (рис. 1.8). Для того чтобы этот газ находился в равновесии, необходимо, чтобы столб газа создавал на пласт давление, равное давлению газа в пласте.

Воспользуемся дифференциальным уравнением гидростатики.

dp=ρ(j_xdx+j_ydy+j_zdz),

где ρ≠const (в отличии от капельной жидкости в данном случае ρ – функция температуры и давления).

Для поля земного тяготения j_x=0; j_у=0; j_z=-g, тогда

dp=-ρgdz.

Как отмечалось, для газа ρ=f(p,T). Для случая покоя газа в скважине можно с некоторым допущением принять процесс сжатия изотермическим, для которого

p_оV_о=pV

или

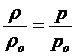отсюда

Подставив в дифференциальное уравнение гидростатики, имеем:

Здесь р_о и ρ_о – известные давление и плотность в известном сечении.

Разделим переменные:

Проинтегрируем:

;

где h – превышение сечения z над z_о (положительное или отрицательное).

Из последнего выражения следует:

отсюда

. (1.10)

Выражение (1.10) не очень удобно для расчетов, поскольку плотность ρ_о, как правило, не известна. Воспользуемся уравнением Менделеева-Клапейрона

pV_m=mR_yT, (1.11)

чтобы приближенно выразить ρ_o/p_o. В уравнении (1.11):

V_m – объем одного моля газа;

R_y – универсальная газовая постоянная, Дж/(град^. кмоль);

Т – абсолютная температура, ⁰К;

т – коэффициент сжимаемости газа, показывающий отклонение поведения газа от идеального.

Разделив обе части уравнения на молекулярный вес газа М и заменив p/ρ на p_o /ρ_o, получим:

; ; .

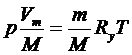В результате –

, (1.12)

следовательно, подставляя (1.12) в формулу (1.10):

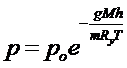. (1.13)

Эта формула известна под именем барометрической.

В расчетной практике часто свойства газов описываются с помощью коэффициента сжимаемости т и относительной плотности газа по воздуху в нормальных условиях .

Для природных газов чаще используется формула:

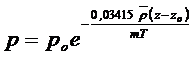, (1.14)

где z-z₀=h.

Для практических расчетов вполне допустимо величину принять равной 10^-4. Тогда формула (1.14) примет вид:

. (1.15)

Формула (1.15) используется при расчете обсадных колонн в условиях газопроявлений. В известной "Инструкции по расчету обсадных колонн" она преобразована к виду:

, (1.16)

где z_y – расстояние от устья до искомого сечения.

По этой формуле можно определить давление газа на любой глубине, если известно давление газа в пласте р_пл.

В частном случае, на устье скважины при z_y=0, давление равно:

. (1.17)

Дата добавления: 2018-06-27; просмотров: 2302; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!