Материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет ее из этого состояния.

Стр 1 из 26Следующая ⇒

Nbsp; МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ УХТИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ П.Ф. Осипов ГИДРОАЭРОМЕХАНИКА БУРЕНИЯ И КРЕПЛЕНИЯ СКВАЖИН Учебное пособие Ухта – 2003 УДК 622.24.051.553/68 О-74 Осипов П.Ф. Гидроаэромеханика бурения и крепления скважин. Части I-III. 2003. – с. Данное учебное пособие состоит из 3-х частей. В I части ("Гидростатика в бурении") объединены разделы, где освещаются вопросы распределения гидростатических давлений в скважине, заполненной полностью или частично различными по реологическим свойствам жидкостями. Приводятся краткие сведения по реологическим и теплофизическим свойствам жидкостей, применяемых в бурении. Часть II ("Гидродинамика буровых промывочных жидкостей") является базовой для изучения гидродинамических процессов в скважине. В ней дано обоснование (иногда адаптированное) предлагаемых к применению расчетных формул. Часть III (Проектирование и оптимизация гидравлических программ буровых процессов) более других "технологична": она объединяет разделы, где освещаются вопросы практического использования знаний, полученных при изучении первых двух частей курса. При этом основное внимание уделено оптимизации гидравлических процессов в скважине на различных этапах ее строительства, которые в технической и учебной литературе освещены явно недостаточно. Учебное пособие ориентировано на подготовку по многоуровневой системе "бакалавр-специалист-магистр" по направлению 553600 – "Нефтегазовое дело". Оно может быть использовано практическими работниками бурения при разработке проектной документации. Рекомендуется для использования в учебных курсах по дисциплинам "Технология бурения нефтяных и газовых скважин", "Гидроаэромеханика при бурении и креплении скважин", "Заканчивание скважин", "Научные основы проектирования режимов бурения", "Осложнения и аварии при бурении нефтяных и газовых скважин", "Физико-химические методы борьбы с осложнениями", " Принципы моделирования в научных исследованиях", а так же для курсового и дипломного проектирования. Рецензенты: кафедра "Бурение нефтяных и газовых скважин" Архангельского государственного технического университета; профессор, доктор технических наук Е.П. Варламов. Учебное пособие печатается в редакции автора. Компьютерная верстка: Осипов П.Ф. …………………………………. Ó УГТУ 2003 Ó Осипов П.Ф. 2003 ОГЛАВЛЕНИЕ Введение...................................................................................................................................... 8 Часть I. Гидростатика в бурении.............................................................................. 19 1. Уравнения гидростатики буровых жидкостей......................................... 19 1.1. Дифференциальное уравнение гидростатики............................................................. 19 1.2. Основные уравнения гидростатики.............................................................................. 20 1.3. Давление жидкости в герметичной скважине при всплытии газового пузыря, поступившего в скважину из пласта.......................................................................................................... 23 1.4. Равновесие газов в скважине......................................................................................... 25 1.5. Относительное равновесие жидкости........................................................................... 27 2. Особенности гидростатики вязкопластичных жидкостей (ВПЖ). 29 2.1. Общие замечания.............................................................................................................. 29 2.2. Расчет "пусковых" давлений на насосах..................................................................... 29 2.3. Определение высоты перепада уровней вязкопластичной жидкости в трубах и заколонном пространстве при спуске и подъеме колонны труб................................................... 31 2.4. Давление на стенки наклонно направленной скважины......................................... 33 2.5. Дегазация бурового раствора......................................................................................... 33 Часть II. Гидродинамика буровых промывочных жидкостей............. 36 3. Общие сведения о потоках в циркуляционной системе скважины. 36 3.1. Основные виды движения. Параметры движения несжимаемой жидкости....... 36 3.2. Гидравлические сопротивления при движении буровых промывочных жидкостей в скважине.............................................................................................................................................. 38 4. Уравнение расхода для структурного режима движения вязкопластичной жидкости в круглой трубе...................................................................................... 41 4.1. Уравнения скорости потока жидкости в круглой трубе........................................... 41 4.1.1. Основное уравнение равномерного движения............................................................ 41 4.1.2. Движение вязкопластичной жидкости. Структурное ядро потока........................... 42 4.1.3. Вывод уравнения, описывающего профиль (эпюру) скоростей в круглой трубе при ламинарном или структурном режиме движения............................................................................. 43 4.1.4. Вывод уравнения профиля скоростей для случая движения вязкопластичной жидкости в круглой трубе при структурном режиме движения................................................................... 45 4.2. Формула Букингэма (уравнение расхода вязкопластичной жидкости)................ 45 4.2.1. Вывод формулы Букингэма........................................................................................... 45 4.2.2. Приведение формулы Букингэма к критериальному виду........................................ 47 5. Методика расчета потерь давления при ламинарном режиме движения вязкопластичных и вязких жидкостей в трубах.................................. 49 5.1. Анализ уравнения Букингэма. Формула Бингама.................................................... 49 5.2. Приведение уравнения Бингама к критериальному виду....................................... 50 5.3. Расчёт линейных потерь давления при ламинарном движении вязких жидкостей в трубах. 51 Комментарий к разделам 4 и 5.............................................................................................. 51 6. Турбулентный режим движения вязких и вязкопластичных жидкостей в трубах.................................................................................................................................... 53 6.1. Кризис структурного режима движения в трубах. Определение критических скорости и расхода............................................................................................................................... 53 6.2. Профиль скоростей при турбулентном режиме движения в трубах и его роль при замещении одной жидкости другой................................................................................................... 53 6.3. Расчет линейных потерь давления при турбулентном режиме движения в трубах. 54 7. Линейные потери давления при движении псевдопластичной ("степенной") жидкости в трубах..................................................................... 55 7.1. Профиль скоростей при ламинарном движении в трубах....................................... 55 7.2. Расчет потерь давления при ламинарном движении................................................ 56 7.3. Потери давления при турбулентном режиме движения степенной жидкости в трубах. 58 8. Потери давления в заколонном пространстве........................................ 60 8.1. Потери давления при ламинарном режиме движения вязких жидкостей в заколонном пространстве..................................................................................................................... 60 8.2. Потери давления при турбулентном режиме движения вязкой жидкости в заколонном пространстве..................................................................................................................... 60 8.3. Потери давления при структурном режиме движения вязкопластичной жидкости в заколонном пространстве............................................................................................... 61 8.4. Кризис структурного режима движения в заколонном пространстве................... 61 8.5. Линейные потери давления при турбулентном движении вязкопластичной жидкости в заколонном пространстве............................................................................................... 62 8.6. Потери давления при ламинарном режиме течения степенной жидкости в заколонном пространстве..................................................................................................................... 62 8.7. Кризис ламинарного режима течения степенной жидкости в заколонном пространстве. 63 8.8. Потери давления при турбулентном течении степенной жидкости в заколонном пространстве.............................................................................................................................................. 63 9. Потери давления, обусловленные наличием соединений труб (замков, муфт)....................................................................................................................................... 65 9.1. Потери давления в соединениях нефтепромысловых труб (внутри их)............... 65 9.2. Потери давления при "обтекании" соединений труб в заколонном пространстве. 67 10. Перепад давления в промывочной системе долот............................. 69 10.1. Методика расчета перепада давления на долоте...................................................... 69 10.2. Влияние подводящего канала на потери давления в промывочных каналах гидромониторных долот................................................................................................. 70 10.3. Расчет коэффициента расхода промывочного узла и распределение жидкости между насадками с различными диаметрами отверстий.................................................... 73 11. Потери давления в манифольде (в обвязке насосов), перепад давления в турбобуре........................................................................................................................... 75 11.1. Расчет потерь и перепадов давления.......................................................................... 75 11.2. Определение коэффициента А обвязки буровых насосов (насосных агрегатов) в условиях буровой............................................................................................................................... 75 12. Гидравлическая характеристика скважины и совмещение ее с гидравлической характеристикой насосных агрегатов............... 76 12.1. Гидравлическая характеристика скважины............................................................ 76 12.2. Гидравлическая характеристика насосных агрегатов........................................... 77 12.3. Совмещение гидравлических характеристик скважины и насосов.................... 79 12.4. Решение задачи совмещения гидравлических характеристик скважины и насосов с учетом технических и технологических ограничений............................................................ 79 12.5. Вопросы рационального использования гидравлической мощности насосов.. 80 13. Расчет параметров промывки скважины и режима работы буровых насосов............................................................................................................................... 82 13.1. Упрощенная методика пересчета параметров промывки при изменении подачи насосов. 82 13.1.1. Вязкопластичные жидкости......................................................................................... 82 13.1.2. Псевдопластичная жидкость........................................................................................ 84 13.2. Вы6op режима работы буровых насосов................................................................... 84 13.3. Расчет эпюры полных (абсолютных) давлений в скважине при промывке..... 84 13.4. Понятие об эквивалентной плотности при промывке и методика ее расчета.. 85 14. Гидродинамические давления, возникающие при движении колонны труб в скважине......................................................................................................................... 87 14.1. Природа возникновения гидродинамических давлений при движении колонны. 87 14.2. Методика определения гидродинамических давлений при равномерном движении труб. 88 14.2.1. Постановка задачи. Вывод уравнения скорости спутного потока.......................... 88 14.2.2. Расчет коэффициента Кск для случая, когда в скважине вязкая жидкость.............. 90 14.2.3. Расчет коэффициента Кск для случая, когда в скважине вязкопластичная (бингамовская) жидкость........................................................................................................................... 91 14.2.4. Расчет коэффициента Кск для случая, когда в скважине псевдопластичная (степенная) жидкость............................................................................................................................................ 94 14.3. Методика расчета допустимой скорости спуска (подъема) "закрытой" колонны в скважине.............................................................................................................................................. 97 Часть III. Проектирование и оптимизация гидравлических программ буровых процессов.......................................................................................................................... 98 15. Расчет гидродинамических давлений при равномерном движении “открытых” трубных колонн в скважине................................................... 98 15.1. Методика расчета гидродинамического давления при равномерном движении “открытой” колонны труб.................................................................................................................... 98 15.2. Расчет допустимой скорости движения “открытой” колонны нефтепромысловых труб. 99 16. Неустановившиеся течения буровых жидкостей в скважине. 100 16.1. Расчет гидродинамических параметров при цементировании обсадных колонн. Прогнозирование отрывного течения....................................................................... 100 16.2. Контроль и управление давлением на забое скважины при газопроявлении. 108 17. Гидромониторные струи и их воздействие на разрушаемую долотом породу................................................................................................................................. 111 17.1. Экспериментальные исследования промывочных узлов гидромониторных долот и затопленных струй......................................................................................................... 111 17.1.1. Экспериментальная установка и методика исследований..................................... 111 17.1.2. Исследование гидравлических сопротивлений промывочных узлов гидромониторных долот 113 17.1.3. Исследование распространения затопленных струй и их динамического воздействия на забой скважины........................................................................................................................ 120 17.2. Фильтрационные потоки в разрушаемой породе, возникающие при воздействии на нее подвижной гидромониторной струи.......................................................................... 122 17.3. Исследование влияния природных и технологических факторов на характеристики фильтрационных потоков на забое скважины....................................................... 127 18. Оптимизация режима промывки скважины............................................ 130 18.1. Традиционная (безоптимизационная) методика проектирования режима промывки скважины при роторном бурении.............................................................................. 130 18.2. Критерии оценки интенсивности промывки забоя скважины.......................... 131 18.3. Оптимизация режима промывки скважины при роторном бурении по критерию J. 134 18.4. Упрощенная (приближенная) методика расчета оптимальных параметров режима промывки........................................................................................................................ 143 18.5. Оптимизация режима промывки скважины при бурении забойными двигателями. 144 18.6. Выбор оптимальных соотношений диаметров скважины и типоразмеров бурильных труб по гидродинамическим критериям................................................................................. 145 19. Оптимизация режима промывки скважины с учётом фактора "утяжеления" восходящего потока в заколонном пространстве выбуренной породой................................................................................................................................................... 151 19.1. Подъём выбуренной породы потоком жидкости в заколонном пространстве. 151 19.2. Влияние выбуренной породы, поступающей в скважину в процессе бурения, на давления при промывке......................................................................................................................... 152 19.3. Оптимизация промывки скважины с учетом фактора "утяжеления" раствора выбуренной породой............................................................................................................................. 154 Список использованных источников............................................................... 154 ПРИЛОЖЕНИЕ. Алгоритмы расчета потерь и перпадов давления в циркуляционной системе скважины.......................................................... 155 Введение. Знание законов гидростатики, гидродинамики, термогидравлики, основ подземной гидравлики, аэродинамики, законов движения и покоя многофазных (чаще двухфазных) жидкостей является приятной привилегией инженера-нефтяника вообще и инженера по бурению глубоких скважин – в особенности. В скважине на различных этапах ее строительства могут находиться в покое или движении разные жидкости: вода, нефть, пластовая вода, насыщенная газом нефть, газ (например, смесь углеводородных газов или воздух), смесь воздуха с буровым раствором, глинистый раствор, различные эмульсии, цементные растворы и т.п. Специалисту по бурению скважин ежедневно приходится решать задачи по прогнозированию поведения скважины с учетом механических, физических и теплофизических свойств жидкостей, находящихся в данный момент времени в скважине. В комплект буровой установки входят буровые насосы, приводная мощность которых исчисляется сотнями киловатт. Рациональное использование этой мощности предполагает выполнение гидравлических расчетов по выбору оптимальной для данных конкретных условий программы промывки при углублении, креплении и испытании скважины. Бурение скважины – это процесс, где промывка скважины и управление давлением жидкости в ней являются основными технологическими операциями, поэтому инженеру-буровику не знать гидромеханику так же безнравственно, как врачу – анатомию человека. В технической литературе, посвященной бурению скважин, дисциплина, которую нам предстоит изучить, обычно называется несколько иначе: "Гидравлика промывочных жидкостей", "Практическая гидравлика в бурении". Иногда называют "Буровая гидравлика", хотя этот термин не отличается строгостью, но ввиду краткости мы будем иногда пользоваться этим названием. Зададимся вопросом: что собой представляет буровая гидравлика и каковы ее место и роль в буровом деле? Теоретические основы буровой гидравлики. Наш предмет, строго говоря, можно было бы назвать механикой жидкостей, применяемых при бурении, креплении и испытании скважин. Из такого названия следует, что он является частью более общей дисциплины "Механики сплошных сред" (и, следовательно, основывается на общих законах механики), которая, в свою очередь, является разделом физики. Перечислим законы и положения механики, на которых основывается буровая гидравлика, как научная дисциплина. Первый закон Ньютона.

Нет нужды доказывать, что под словами "материальная точка" понимается частица (пусть бесконечно малая) не только твердого тела, но и жидкости или газа. Справедливости ради следует сказать, что этот закон был установлен еще Галилеем за 100 лет до Ньютона.

Второй закон Ньютона.

Скорость изменения количества движения материальной точки (mu) равна действующей на нее силе F, то есть

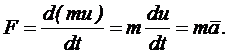
Этот закон, как известно, считается в физике (разумеется, классической) основным законом динамики материальной точки. Можно предложить более строгую формулировку закона.

Результирующая сила, действующая на материальную точку, равна массе, умноженной на ускорение, и совпадает по направлению с направлением ускорения.

Из второго закона Ньютона, как следствие, выходит легко доказуемая теорема об изменении количества движения.

Изменение количества движения материальной точки за некоторый промежуток времени равно импульсу действующей на эту точку силы:

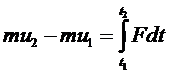Третий закон Ньютона.

Всякое действие тел друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга взаимодействующие тела, всегда равны по величине и противоположны по направлению.

Часто этот закон, упрощая, называют законом действия и противодействия, что и не точно, и не строго.

Закон независимости действия сил. Иногда этот закон называют четвертым законом Ньютона.

Если на материальную точку действует одновременно несколько сил, то ускорение этой точки равно геометрической сумме тех ускорений, которые получает эта точка при действии каждой из этих сил в отдельности.

Теорема о кинетической энергии.

Изменение кинетической энергии mu²/2 движущейся материальной точки равно работе приложенных к ней сил на пройденном этой точкой пути L.

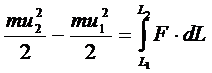
Буровая промывочная жидкость – как объект изучения гидромеханики. Силы действующие на жидкость.

В отличие от гидротехников, гидромелиораторов, машиностроителей, механиков, которые обычно ограничиваются изучением законов статики и динамики жидкостей типа воды, керосина, масел и т.п., которые называются вязкими (ньютоновскими) жидкостями, инженер по бурению скважин имеет дело еще и с такими жидкостями, у которых в некоторой степени проявляются свойства, присущие твердым телам: прочность, упругость и т.п. Кроме того, приходится иметь дело с сжимающимися флюидами – различными газами или смесями последних с капельными жидкостями.

Жидкость в гидравлике вообще и в буровой гидравлике, в частности, рассматривается как совокупность материальных точек (частиц) в ограниченном объеме. Принимается, что материальные частицы жидкости заполняют пространство без пустот и разрывов. В этом заключается суть тезиса о непрерывности и сплошности жидкой среды. Сказанное полностью относится к буровым промывочным жидкостям любого типа, включая аэрированные. Из сказанного следует, что реальная жидкость заменяется на ее модель, причем модели могут изменяться (усложняться или упрощаться) в зависимости от целей исследований.

Буровой раствор является, как правило, суспензией: твердые частицы (глина, выбуренная порода, утяжелитель) взвешены в жидкости и не осаждаются в ней под действием сил тяжести. Такие суспензии называют седиментационно устойчивыми, несмотря на то, что плотность твердых частиц, равномерно распределенных в жидкой фазе, кратно превышает плотность жидкости. Устойчивость таких сред и дает возможность заменить реальную жидкость с явно выраженным дискретно меняющимся распределением массы, на модельную жидкость, имеющую плотность, равную средней плотности бурового раствора, подчиняющуюся тезису о непрерывности (сплошности) среды. Это позволяет рассматривать все механические характеристики жидкой среды (плотность, давление, скорость и т.д.) как функции координат точки пространства и времени, причем в большинстве случаев эти функции предполагаются непрерывными и дифференцируемыми.

На выделенный внутри жидкости некоторый объем, находящийся в равновесии (в покое или в состоянии динамического равновесия) действуют силы, которые бывают двоякого рода: поверхностные и объемные.

Поверхностные силы, как следует из названия, - это такие силы, которые распределены по поверхности выделенного объема и по своей величине пропорциональны этой поверхности. К ним относятся силы упругости, поверхностного натяжения, вязкости, давления окружающей среды и т.п.

Объемные (массовые) силы действуют на всю массу жидкости. Пример: силы тяжести, силы инерции и т.п.

И те и другие приводят к возникновению деформаций и, следовательно, напряжений. В гидромеханике нормальные напряжения (от сил, действующих нормально к элементарной площадке) принято называть давлением. В покоящейся жидкости это давление называют обычно гидростатическим, а в движущейся – гидродинамическим.

Свойства жидкостей. Элементы реологии.

Выше уже отмечалось, что в бурении применяют разные жидкости. Отличаются они не только цветом и химическим составом. С точки зрения гидравлики они различны тем, что по-разному ведут себя в состоянии покоя или движения. Поэтому рассмотрим только те свойства жидкостей, которые помогут нам количественно охарактеризовать эти состояния.

Плотность.

Если капельная жидкость в выделенном объеме однородна, то плотность, как известно, определяется отношением

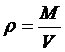где М – масса жидкости в объеме V.

В покоящемся или движущемся газе ρ зависит от координат. Тогда

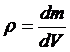
где dm – масса элементарного объема dV.

Вязкость. Реологические параметры.

Самым важным для гидравлики является свойство жидкости оказывать сопротивление перемещению одной частицы относительно другой, иначе говоря, сопротивляться сдвигу. Это свойство определяется общим понятием "вязкость". Это понятие хорошо известно из курсов физики и общей гидравлики.

Представим себе, что некоторое количество жидкости заключено между двумя плоскими параллельными пластинами, одна из которых перемещается относительно другой со скоростью du при расстоянии между пластинами dy. Для того чтобы поддерживать равномерное движение пластины, к ней должна быть приложена сила F, затрачиваемая на преодоление сил внутреннего трения в жидкости.

В 1723 г. И. Ньютон высказал предположение, впоследствии блестяще подтвержденное опытом (Петров И. П.), которое, в конечном счете, сводится к зависимости

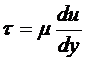(В.1)

Иначе говоря, И. Ньютон предположил, что касательное напряжение в жидкости при слоистом, упорядоченном течении прямо пропорционально градиенту скорости. Коэффициент пропорциональности μ принимается за меру вязкости и характеризует это свойство жидкости.

Уравнение (В.1) – это математическое выражение ньютоновской модели жидкости. Из формулы следует, что μ – это сила трения, приходящаяся на единицу поверхности трения, при градиенте скорости равном единице.

Для того чтобы жидкость полностью подчинялась ньютоновской модели, необходимо, чтобы величина μ не зависела от градиента скорости du/dy. Это, в частности, означает, что с увеличением скорости жидкость и не разжижается, и не становится более вязкой. Зависимость

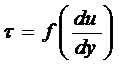
в таких случаях графически изображается в виде прямой, исходящей из начала координат.

В бурении, кроме вязких, "ньютоновских", применяются жидкости, не подчиняющиеся этому закону. Такие жидкости принято называть аномальными. Все они делятся на две большие группы (системы): реологически стационарные и реологически нестационарные. Жидкость будет реологически стационарной, если вид зависимости 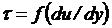у таких жидкостей не зависит от времени.

Экспериментально полученный график зависимости 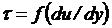называется реологической кривой или реограммой. Приборы, предназначенные для получения реологических кривых (реограмм) и реологических констант называют вискозиметрами. Наибольшее распространение получили ротационные вискозиметры в силу их простоты конструкции и эксплуатации.

Приборы, предназначенные для измерения реологических свойств аномальных жидкостей, часто называют (в отличие от вискозиметров для ньютоновских жидкостей) пластомерами или реометрами.

Нашли применение, кроме ротационных, капиллярные вискозиметры (реометры).

Недостатки и преимущества ротационных и капиллярных вискозиметров детально описаны в книге [2].

В реологии буровых промывочных жидкостей широко применяются ротационные вискозиметры, в частности, вискозиметр ВСН-3 (безнадежно морально устаревший). Прибор представляет собой цилиндрический сосуд, в который соосно помещается другой цилиндр, образующий кольцевой зазор с первым. В этот зазор помещается испытуемая жидкость. Внутренний цилиндр подвешивается на упругой нити (пружине). Внешний цилиндр может вращаться с различной скоростью (дискретно). В кольцевом зазоре, в находящейся в нем жидкости возникают сдвиговые деформации при известном градиенте скорости (поскольку известна окружная скорость движения внешнего цилиндра по отношению к внутреннему цилиндру ∆u и известен размер зазора ∆у). Силы внутреннего трения передаются внутреннему цилиндру, возникает вращающий момент, пропорциональный величине τ, приводящий к закручиванию упругой пружины на угол φ, являющийся мерой τ. Изменение частоты вращения п сопровождается изменением φ.

Главным недостатком отечественных реометров является ограниченность и предопределенность скоростей вращения внешнего цилиндра, что ограничивает число опытных точек.

Известны более совершенные зарубежные многоскоростные реометры и реометры с плавным изменением скорости вращения с регистрацией скорости вращения и момента.

Теория ротационной вискозиметрии изложена в работе [2].

Исследования, проведенные на реометрах, показали, что реологическое поведение жидкостей различно. На рис. В.1 показаны типичные реограммы реологически стационарных систем. Прямая 1 на рис. В.1а – это типичная зависимость между τ и градиентом скорости du/dy, соответствующая модели Ньютона (В.1).

Кривые 2 и 3 на этом же рисунке – это графическое отображение псевдопластичной ("степенной") реологической модели жидкости Оствальда-де-Ваале и соответствуют уравнению

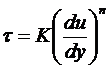. (В.2)

При п<1 (кривая 2) с увеличением градиента скорости сдвига прирост τ уменьшается, сопротивление жидкости сдвигу уменьшается, она становится менее вязкой. Угловой коэффициент прямой ОВ₁

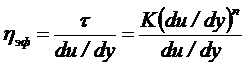(В.3)

является мерой вязкости жидкости при определенном градиенте, соответствующим точке В₁ и называется эффективной вязкостью η_эф. С увеличением градиента величина η_эф уменьшается. Следовательно, коэффициент η_эф – величина переменная и зависящая от du/dy. В точке В₂ жидкость, таким образом, приобретает новые свойства. Получается так, что жидкость имеет переменную вязкость, если сравнивать ее поведение с поведением ньютоновской жидкости. Иначе говоря, псевдопластичная жидкость (равно как и все другие аномальные жидкости) – это как бы ньютоновская жидкость с переменной вязкостью η_эф.

Жидкости, вязкость которых уменьшается с увеличением du/dy, весьма интересны с позиции задач бурения скважин. Установлено, что буровые растворы, обработанные полимерами, приобретают свойства псевдопластичной жидкости.

Если поведение аномальной жидкости соответствует кривой 3, то такая жидкость называется дилатантной. Для нее характерно увеличение вязкости с ростом du/dy. Это значит, что математически модель жидкости может описываться степенной функцией с показателем степени п>1.

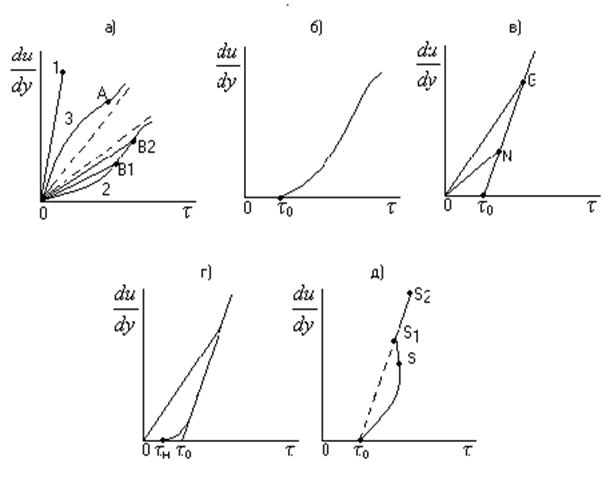
Рис. В.1. Реограммы реологически стационарных жидкостей:

а – вязкая (ньютоновская) (1), псевдопластичная (2), дилатантная жидкости; б – вязкопластичная жидкость (модель Кэссона-Шульмана); в - вязкопластичная жидкость (модель Бингама); г - вязкопластичная жидкость (модель Шведова); д – тиксотропно-вязкопластичная жидкость.

Эффективная вязкость диалатантных жидкостей η_эф, таким образом, растет с увеличением градиента скорости (расхода жидкости). Такие "густеющие" по мере прокачки жидкости не представляют интереса для бурения, применение их явно не желательно.

Надо оговориться, что степенная зависимость применима только на участках 0А и 0В₂, т.е. до точек перегиба кривых 2 и 3 на рис. В.1а.

Для реологических моделей жидкостей, показанных на рис. В.1а, характерно отсутствие начальной прочности, они полностью лишены свойств, присущих твердым телам. Это видно из того, что все кривые, как и прямая 1, выходят из начала координат.

На рис. В.1б...В.1д показаны реограммы аномальных, реологически стационарных жидкостей, характерной особенностью которых является то, что кривые отсекают от оси τ положительный отрезок, равный τ_о.

Жидкость, реограмма которой показана на рис. В.1б, называется вязко-пластичной, соответствующей модели Кэссона-Шульмана:

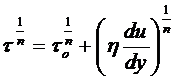(В.4)

Если реограмма представляет собой прямую (рис. В.1в), то такая жидкость называется жидкостью Бингама. Математически модель определяется уравнением:

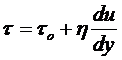. (В.5)

Шведов показал, что часть жидкостей ведет себя в соответствии с реограммой, показанной на рис. В.1г. Как видим, она состоит из двух участков: кривой (подобно модели Кэссона-Шульмана) и прямой, схожей с моделью Бингама. Для характеристики реограммы Шведова необходимо и достаточно знать три параметра: τ_н, τ_о и η. Заметим, что для модели Бингама достаточно знать τ_о и η. Обычно криволинейной частью реограммы Шведова пренебрегают, и тогда модель превращается в модель Бингама с действительной областью выше точки С. область градиента скорости от 0 до точки С считается недействительной, говоря точнее, редко встречающейся на практике. В итоге как бы объединяются две модели в одну, поэтому в технической литературе такую модель часто называют моделью жидкости Шведова-Бингама.

Можно выделить еще одну модель – так называемую тиксотропно-вязко-пластичную жидкость, типовая реограмма которой показана на рис. В.1д.

Следует обратить внимание на то, что угловые коэффициенты прямых на рис. В.1в, В.1г и угловой коэффициент прямой τ_о-S₂ (рис. В.1д) являются величинами, характеризующими жидкость. Этот коэффициент называется структурной (или пластической) вязкостью и обозначается буквой η.

Величина τ_о называется динамическим напряжением сдвига.

Реологически нестационарные системы в буровой практике встречаются значительно чаще, чем реологически стационарные. (Правда, в последнее время, в связи с широким внедрением малоглинистых и полимерных систем, такое утверждение становится все более сомнительным). Глинистые буровые растворы (глинистые суспензии), строго говоря, не являются реологически стационарными системами. Дело в том, что прочность их зависит от времени. Находясь в покое, глинистый раствор упрочняется, в нем происходит процесс восстановления связей между коллоидными частицами. Под влиянием взаимодействия частиц дисперсной фазы между собой и молекулами дисперсной среды в системе образуется структура. Такое свойство жидкостей называется тиксотропией, а структура – тиксотропной. При движении жидкости возникшие ранее связи в структуре разрушаются, прочность структуры уменьшается, и этот процесс идет быстрее при больших градиентах скорости. "Разжижение" при заданном градиенте скорости сдвига происходит не сразу. Необходимо определенное время, чтобы прочностные и вязкостные показатели стабилизировались, наступило динамическое равновесие между процессами структурообразования и разрушения.

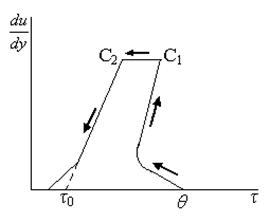
Рис. В.2. Пример реограммы реологически нестационарной жидкости.

Характерной особенностью реологически нестационарных систем является явно выраженный гистерезис. На рис. В.2 показан реометрический эксперимент с системой, имеющей статическое напряжение сдвига (прочность структуры) равное θ. Стрелками показано направление изменения скорости. Участок С₁С₂ – это выдержка во времени системы на верхней границе по градиенту скорости, при которой происходило "разжижение" системы (в вискозиметре поддерживается постоянная скорость вращения до того момента, пока не стабилизируется показание по углу поворота пружины φ). Ниспадающая кривая, таким образом, является реограммой системы, тиксотропная структура которой предварительно разрушена (на участке С₁С₂).

Математические модели реологически нестационарных систем создать очень сложно в связи с тем, что в уравнение должно войти время t.

Тиксотропные свойства бурового раствора способствуют удержанию твердых частиц во взвешенном состоянии при остановке насосов и прекращении промывки скважины. До недавнего времени этому свойству жидкости предавали явно преувеличенное значение. Массовое бурение скважин с промывкой водой (Татария, Башкирия, Средняя Волга) показало, что при использовании ньютоновских жидкостей, абсолютно лишенных тиксотропных свойств, можно обеспечить удовлетворительную очистку ствола скважины. Передовая инженерная мысль в настоящее время склоняется к применению жидкостей с весьма ограниченными тиксотропными свойствами, следовательно, тяготеющих в большей степени к реологически стационарным системам. Широко распространенные полимер-глинистые системы с малым содержанием твердой фазы почти не обладают тиксотропными свойствами. Что касается реологической модели, то, как уже говорилось ранее, предпочтение отдается псевдопластичной жидкости, вязкость которой уменьшается с увеличением скорости сдвига.

В работе [2] приведен список фундаментальных моделей, среди которых, кроме уже упомянутых, есть модель де Хавена вида:

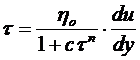, (В.6)

частным случаем которой является модель Рабиновича:

. (В.7)

Эти модели представляют большой интерес для задач буровой гидравлики, поскольку могут полностью заменить собой степенную модель и их разновидности.

На кафедре бурения УГТУ на основе модели де Хавена предложены несколько нетрадиционных реологических моделей буровых жидкостей:

, (В.8)

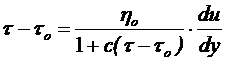, (В.9)

, (В.10)

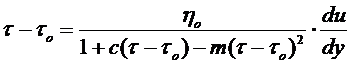. (В.11)

Модель (В.8) является упрощенным вариантом общей модели де Хавена при n=1. Она вполне может заменить степенную модель, если окажется, что на ее основе можно получить уравнение расхода для ламинарного течения (формулу для определения линейных потерь давления). Так же, как и степенная модель, она двухпараметрическая, но имеет то неоспоримое преимущество, что действительно при любых градиентах скорости.

Модель (В.9) трехпараметрическая и может заменить трехпараметрическую модель Гершеля-Балкли:

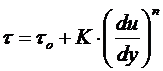, (В.12)

которой присущи те же недостатки, что и степенной модели.

Модель (В.10) отличается от остальных тем, что может отразить давно обнаруженное в эксперименте замедление процесса разжижения (вплоть до прекращения последнего) при высоких скоростях сдвига, граничащих с переходом на турбулентный режим движения.

Наконец, четырехпараметрическая модель (В.11). Она универсальная и в принципе может отобразить все возможные реограммы, полученные при исследовании буровых промывочных жидкостей. Основной недостаток: большое число реологических параметров.

Общим недостатком всех "степенных" моделей, в уравнении которых градиент скорости возводится в степень меньше единицы, является то, что они заведомо неприменимы при (du/dy)≤1. Причина чисто формальная, математическая. Дело в том, что при (du/dy)=1 все кривые, независимо от величины n, сходятся в одну точку, а при (du/dy)≤1 величины t, найденные по формуле (В.2), получаются больше, чем по формуле (В.1), что делает делает модели не применимыми в оласти 0≤(du/dy)≤1. Печальным следствием этого является то, что корректность результатов применения моделей ставится в зависимость от размерности градиента скорости сдвига.

Однако есть еще один принципиальный недостаток степенных моделей. Он заключается в том, что так называеый параметр (индекс, показатель, коэффициент) консистентности K в формуле (В.2) не имеет определенного физического смысла. По размерности он совпадает с размерностью динамической вязкости. По логике подхода он должен быть равен вязкости μ "исходной", не поддающейся разжижению ньютоновской жидкости, с которой сравнивается исследуемая разжижаемая жидкость, но на самом деле этого нет.

Модели жидкостей {(В.8)…(В.11)} в этом отношении имеют несомненное преимущество перед степенными. Реологический параметр η_о по физическому смыслу (и в отличие от формального параметра K), является начальной вязкостью исследуемой жидкости при градиентах скорости сдвига, близких к нулю. А это дорогого стоит.

В технической литературе по бурению для решения инженерных задач в области гидромеханики чаще других используется модель Шведова-Бингама (причина в том, что реологические параметры имеют четкую смысловую нагрузку):

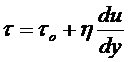Тем самым вводятся следующие допущения:

- буровые промывочные жидкости суть реологически стационарные системы, по крайней мере, становятся таковыми вскоре после начала движения;

- большинство буровых промывочных растворов, относящихся к аномальным жидкостям, удовлетворительно описываются моделью Шведова-Бингама.

Разумеется, не во всех задачах, не для всех жидкостей, применяемых в бурении, такие допущения корректны. В ряде случаев более точные решения могут быть получены с использованием степенных уравнений (модель Оствальда-де-Ваале или модель Кэссона-Шульмана), хотя, как только что было сказано, в области небольших градиентов скорости они вообще не применимы или приводят к недопустимым погрешностям.

Реологические параметры буровой промывочной жидкости зависят от температуры в скважине. Строго говоря, в скважине находится не одна жидкость, а бесконечное их множество в связи с тем, что температура раствора непрерывно меняется по мере его движению к забою и обратно. Вместе с температурой меняются все параметры: θ, τ_о, η. При этом не исключено, что "меняется" и сама жидкость в отношении реологической модели.

В заключение несколько слов о том, зачем нужны математические модели поведения различных жидкостей при их деформации в форме сдвига. Покажем это на примере. В курсе "Гидравлика" выводится формула Пуазейля-Гагена для расчета потерь давления при напорном ламинарном движении воды, например, по трубам. Формула получается аналитически, исходя из модели Ньютона. Она замечательно подтверждается экспериментально. Забегая чуть вперед скажем, что аналогичные решения могут быть найдены, если воспользоваться другими моделями, например, моделью Шведова-Бингама, степенной моделью, моделями по формулам (В.8), (В.9) и (В.10).

Сжимаемость жидкостей.

Капельные жидкости под воздействием давления меняют свой объем. Это свойство характеризуется коэффициентом объемного сжатия β_V, представляющим собой относительное изменение объема жидкости на изменение давления на единицу:

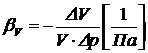(В.13)

Величина, обратная β_V называется модулем объемного расширения k_V [Па].

Температурное расширение оценивается коэффициентом объемного расширения β_t:

. (В.14)

Уравнение состояния идеального газа.

Перегретый газ, к которому можно отнести воздух или природный газ со значительным содержанием метановой фракции, в первом приближении может быть описан уравнениями состояния идеального газа, обобщенной формой которых является закон Клайперона-Менделеева:

, (В.15)

где p – абсолютное давление; V – объем газа, имеющего массу т; М – молекулярный вес газа; Т – температура по шкале Кельвина; R_m – универсальная газовая постоянная.

Теплофизические свойства буровых растворов.

Теплофизические свойства любого вещества связаны между собой следующим соотношением:

λ_т=асρ, (В.16)

где λ_т – коэффициент теплопроводности; а – коэффициент температуропроводности; с – удельная теплоемкость; ρ – плотность.

Коэффициент λ выражает то количество тепла в джоулях, которое проходит в течении одной секунды через стенку толщиной в 1 м и площадью 1 м² при разностях температур на поверхностях стенки, равной 1⁰С.

Удельная теплоемкость с вещества представляет собой то количество тепла Q_т, которое необходимо для нагревания единицы количества вещества m на 1⁰С:

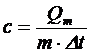. (В.17)

Коэффициент температуропроводности "а" характеризует собой скорость изменения температуры единицы объема среды, то есть изменение ее температуры за единицу времени. Из (1.8) имеем:

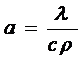. (В.18)

Теплофизические свойства буровых растворов начали всерьез определять только после 1962. Установлено, что величина удельной теплоемкости с уменьшается с увеличением плотности и находится в пределах от 0,86 до 0,40 ккал/(кг×⁰С) или, что то же самое, от 3,68∙10³ до 1,67∙10³ Дж/(кг×⁰С). Объясняется это тем, что глина обладает низкой по сравнению с водой теплоемкостью (около 0,22 ккал/(кг×⁰С) или 0,92∙10³ Дж/(кг×⁰С) и снижает первоначальную теплоемкость воды (4,19∙10³ Дж/(кг×⁰С).

Предложена эмпирическая формула для определения удельной теплоемкости водных суспензий глины:

С=[0,334+0,6745ρ^-3,3]∙4,19∙10³Дж/(кг×⁰С). (В.19)

где ρ – плотность суспензии в г/см³.

Ниже приводится список условных обозначений переменных и констант, использованных в работе.

Условные обозначения переменных и констант
Средняя скорость потока в трубах	v_в
Внутренний диаметр канала в трубах	d_в
Порядковый номер элемента	i
Длина i-тогоэлемента	e_i
Минимальный диаметр канала в соединении	d_c
Плотность жидкости	r
Параметр (критерий) Рейнольдса для потока в трубе	Re_в
Критерий (критерий) Хёдстрема для потока в трубе	He_в
Критерий Сен-Венана - Ильюшина (для трубы)	Sen_в
Индекс (показатель) консистенции псевдопластической (степенной) жидкости	K
Показатель нелинейности (степенная жидкость)	n
Диаметр скважины	D
Коэффициент гидравлического сопротивления	l
Критическая скорость движения жидкости в трубах	v_в.кр
Критический расход в трубах	Q_в.кр
Критическая скорость жидкости в заколонном пространстве	v_к.кр
Критический расход в заколонном пространстве за трубами	Q_к.кр
Площадь сечения заколонного пространства	F_кр
Критическая скорость жидкости в заколонном пространстве за соединениями (муфтами, замками)	v_км.кр
Критический расход жидкости в заколонном пространстве за соединениями (муфтами, замками)	Q_м.кр
Расход жидкости в циркуляционной системе (подача насосов)	Q
Коэффициент относительных потерь давления в соединениях	K_м
Длина одной трубы	l_o
Наружный диаметр трубы	d_н
Наружный диаметр соединения (муфты, замка)	d_м
Критерий Рейнольдса для вязкой жидкости	Re
Критерий Рейнольдса (приведенный) для трубы при течении вязкопластичной жидкости	Re_в*
Критерий Сен-Венана	Sen
Критерий Хёдстрема	He
Потери давления в трубе	p_в
Потери давления в заколонном пространстве	p_к
Потери давления в заколонном пространстве за трубами	p_к.т
Потери давления местные в заколонном пространстве за замками (муфтами)	p_к.мм
Потери давления линейные в заколонном пространстве за замками (муфтами)	p_к.м
Потери давления в заколонном пространстве за забойным двигателем	p_к.тб
Общие потери давления в циркуляционной системе (без потерь в обвязке насосов)	p_п
Потери давления в обвязке насосов (в манифольде)	p_обв
Допустимые потери в заколонном пространстве	p_к.доп
Перепад давления в забойном двигателе	p_тб
Средняя скорость движения жидкости в заколонном пространстве	v_к
Перепад давления на долоте	p_д
Коэффициент потерь давления в обвязке насосов, Па*с²/(м³/кг)	A_обв
Критическая скорость жидкости в заколонном пространстве за забойным двигателем	v_к.тб.кр
Критический расход жидкости в заколонном пространстве за забойным двигателем	Q_к.тб.кр
Длина забойного двигателя	l_тб
Наружный диаметр забойного двигателя	d_тб
Коэффициент, характеризующий зависимость перепада давления на турбобуре от расхода	A_тб
Коэффициент расхода промывочных каналов долот	m_н
Площадь забоя скважины	F_д
Скорость движения колонны труб в скважине	u_т
Эквивалентная скорость	u_экв
Расход жидкости, соответствующий эквивалентной скорости	Q_экв
Рациональный (рекомендуемый) расход жидкости	Q_рц
Коэффициент наполнения насосов	b
Допустимое давление для цилиндровых втулок насоса данного диаметра	p_вт
Диаметр отверстия гидромониторных насадок долот	d_o
Число используемых насадок в долоте	z
Диаметр отверстия подводящего канала долота	d_п
Суммарная площадь промывочных отверстий долота	f_д
Удельный расход жидкости (приходящийся на единицу площади забоя), (м³/с)/м²	q
Обобщенный коэффициент потерь давления в трубах при ламинарном движении степенной жидкости, Па/(м³/с)	S_в
Обобщенный коэффициент потерь давления в заколонном пространстве при ламинарном движении степенной жидкости, Па/(м³/с)	S_к
Пластовое давление	p_пл
Коэффициент аномальности пластового давления	k_а
Плотность не минерализованной воды	r_в
Длина струи (от насадки до забоя)	l_с
Коэффициент расширения струи	a_o
Эквивалентный расход бурового раствора за соединениями труб (муфтами, замками)	Q_мэ
Гидродинамическое (избыточное) давление при спуске колонны труб	p_гд.с
Гидродинамическое (избыточное) давление при подъеме колонны труб	p_гд.п
Обобщенный коэффициент гидродинамических сопротивлений при спуске (подъеме) колонны труб	С
Вязкопластичная (бингамовская) жидкость	ВПЖ
Псевдопластичная (степенная) жидкость	ППЖ

Часть I. Гидростатика в бурении.

Дата добавления: 2018-06-27; просмотров: 528; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!