Профиль скоростей при ламинарном движении в трубах.
Реологическая модель псевдопластичной жидкости выражается уравнением:
. (7.1)
Реологическая функция:
. (7.2)
Рис. 7.1. Изменение скорости по сечению потока степенной жидкости при одном и том же перепаде давления.
Условия расчета: потери давления 1000 Па; длина трубы – 1000 м; диаметр трубы 200 мм; коэффициент консистентности 0,036 Па*с.
Подставив это выражение в дифференциальное уравнение (4.10) и решив его в пределах изменения у от 0 до R, получим:
. (7.3)
При n = 1 это уравнение превращается в формулу (5.8).
Реологическая модель (7.1) подразумевает отсутствие прочности структуры (tо= 0) и, следовательно, отсутствие структурного ядра. Применительно к буровым растворам для бурения n всегда меньше 1. На рис. 7.1. показано, как изменяется профиль скорости по сечению потока при различных значениях n и неизменной величине коэффициента консистентности K. Все эпюры следует сравнивать с параболой,соответствующей n=1,0. С уменьшением n наблюдается деформация профиля, который становится все более приплюснутым в центре и более крутым на периферии. С уменьшением n показатель степени при у и R увеличивается и, например, при n=0,4 становится равным 3,5.
С точки зрения замещения одной жидкости другой при ламинарном течении очевидно более предпочтительными представляются "степенные" жидкости с меньшими значениями n.
|
|
|
Примечание: здесь уместно напомнить о недостатках степенной модели, о чем говорилось в "Ведении" и будет сказано в следующем подразделе.
Расчет потерь давления при ламинарном движении.
Для получения расчетной формулы, как было показано ранее, необходимо составить уравнение расхода с использованием функции (7.3):
.
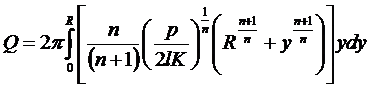Интегрирование этого уравнения с последующей заменой R на d даст следующий результат:
. (7.4)
После несложных преобразований:
. (7.4)'
При использовании v вместо Q формула примет вид:
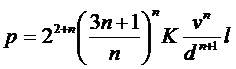. (7.5)
Оценим, как влияет изменение Q на изменение p. Из формул (7.4) и (7.5) следует, что при n <1 темп роста p отстает от темпа увеличения Q. Сравним это с вязкой жидкостью, где между Q и p линейная зависимость. Получается, что использование степенной жидкости с энергетической точки зрения весьма выгодно. Вместе с тем результаты расчета, приведенные на рис. 7.2, свидетельствуют о том, что такое утверждение не всегда справедливо.
Из рис. 7.2 видно, что при расходах менее 1 дм3/с потери давления, найденные по формулам (7.4) или (7.4)' существенно больше, чем при движении вязкой жидкости с n=1, вязкость которой равна 0,4 Па*с. Разумеется, такой вывод противоречит практике. Видно также, что при Q, равном приблизительно 0,9…1,0 дм3/с потери давления не зависят от показателя нелинейности, что тоже вызывает возражение. И только при Q > 1 дм3/с начинается "ожидаемое" уменьшение потерь давления.
|
|
|
Вывод очевиден: расчетные формулы, полученные на основе так называемой степенной реологической модели, не применимы при малых расходах, где они дают либо противоречащие здравому смыслу результаты, либо приводят к недопустимым погрешностям (в сторону завышения потерь). Пробные расчеты показали, что расход жидкости, соответствующий пересечению линий давления зависит преимущественно от диаметра труб: с уменьшением диаметра он тоже уменьшается.
Из анализа рис. 7.1 и 7.2 следует принципиально важный вывод об отсутствии логической связи между коэффициентом консистентности и динамической вязкостью вязкой жидкости, с которой сравнивается реологическое поведение псевдопластичной жидкости. Величина K не имеет физического смысла. Это не вязкость жидкости-прототипа, хотя и имеет размерность вязкости. Коэффициент К следует рассматривать только как коэффициент уравнения аппроксимации, полученного при реологических исследованиях. Одно и то же исследование может быть описано (с сопоставимыми показателями тесноты связи) различными комбинациями K и n, использование которых для определения потерь даст совершенно разные результаты, в том числе явно нелепые. Ясно, что такой результат отражает несовершенство уравнения (7.1), с помощью которого пытаются описать реологическое поведение жидкостей, называемых псевдопластичными.
|
|
|
7.3. Потери давления при турбулентном режиме движения
степенной жидкости в трубах.
В настоящее время нет единого, общепринятого, метода определения потерь давления при движении степенной жидкости в турбулентном режиме.
Е.Г. Леонов и В.И. Исаев (Гидроаэромеханика в бурении. М.: Недра, 1987) предлагают традиционный метод - использование формулы Дарси-Вейсбаха. При этом величину l советуют вычислять по известной формуле Блазиуса
λ=0,3164/Re0,25,
а для шероховатых труб – по формуле Альтшуля, которые, строго говоря, предназначены для вязких жидкостей.
Известна ещё одна методика, менее всего теоретически обоснованная, но вполне допустимая к применению для инженерных расчетов. Суть её сводится к формуле:
|
|
|
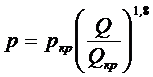, (7.6.)
где
. (7.7)
Сравним теперь формулы (7.7) и (7.4)'. Обнаружим без труда, что pкр - это потери давления при ламинарном режиме, но при Q = Qкр. Иначе говоря, "последние" потери давления перед переходом в турбулентный режим.
Методика расчета будет окончательно сформулирована, если дать формулу для определения Qкр.
В упомянутом учебнике Е.Г. Леонова и В. И. Исаева предлагается формула:
. (7.8)
Н. Маковей (Гидравлика бурения. М.: Недра, 1986) считает, что более других подтверждается опытными данными методика, основанная на определении Reкр :
, (7.9)
где
.
Турбулентный режим наступает, когда Reст > Reкр , где Reст - приведенное (для степенной модели) число Рейнольдса, определяемое по формуле:
. (7.10)
В момент, когда Reст = Reкр , Q = Qкр .
Следовательно,
. (7.11)
8. Потери давления в заколонном пространстве.
Характерной особенностью заколонного (кольцевого) пространства, по которому движется (чаще всего, снизу-вверх) жидкость, является геометрическая неопределенность. В обсаженной части диаметр скважины известен, но никто не может точно описать отклонение оси труб от оси скважины на различных участках колонны труб, тем более - при ее вращении. В необсаженной части скважины, где практически всегда есть каверны и сужения, почти невозможно говорить о точных геометрических размерах скважины. В такой обстановке трудно настаивать на применении точных расчетных методик определения линейных потерь давления, предусматривающих, например, строго концентричное расположение внутренней трубы по отношению к оси скважины. Без ущерба для точности результатов расчета вполне можно ограничиться приближенными методами. В частности, вполне допустимо применение принципа гидравлического радиуса, чтобы использовать ранее полученные формулы для трубных каналов.
8.1. Потери давления при ламинарном режиме движения
вязких жидкостей в заколонном пространстве.
При промывке скважины водой ламинарный режим практически невозможен потому, что критические расходы весьма малы. Более вероятно "встретить" ламинарный режим при промывке обсаженной скважины через насосно-компрессорные трубы, например, нефтью.
Критический расход в кольцевом (заколонном) пространстве вычисляется по формуле:
, (8.1)
где D и dн - соответственно диаметр скважины и наружный диаметр трубы.
При Q < Qкр (движение ламинарное) потери давления можно определить по формуле Пуазейля-Гагена:
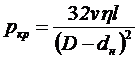(8.2)
или, если выразить среднюю скорость vк через расход Q и сечение кольцевого канала, - по формуле:
. (8.3)
Разумеется, правомерен традиционный путь определения рк по формуле Дарси-Вейсбаха:
, (8.4)
где
, (8.5)
а
. (8.6)
8.2. Потери давления при турбулентном режиме движения
вязкой жидкости в заколонном пространстве.
В силу указанных выше обстоятельств, касающихся несоосности труб по отношению к скважине и наличия каверн и сужений, практически не поддающихся количественной оценке, есть все основания использовать для определения коэффициента гидравлических сопротивлений lк формулу Б.И. Мительмана, которая была им предложена для маловязких глинистых растворов нормальной плотности (не более 1200 кг/м3).
. (8.7)
Искомые потери давления можно определить либо по формуле (6.4), либо по формуле:
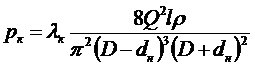. (8.8)
При промывке скважины технической водой допускается величину λк принимать постоянной и равной 0,024.
8.3. Потери давления при структурном режиме движения
вязкопластичной жидкости в заколонном пространстве.
Известен так называемый точный метод решения этой задачи, преложенный Гродде и описанный применительно к течению ВПЖ в трубе в разделе 2. Вначале вычисляют критерий Сен-Венана для кольцевого канала:
. (8.9)
Затем по вспомогательному графику функции b = f(Sen) определяют b и после этого - искомое значение рк :
. (8.10)
При наличии ЭВМ рекомендуется вычислять pк численным методом на основе точного решения Букингэма – по формуле (4.21).
Нам представляется (учитывая большую неопределенность в геометрическом описании заколонного пространства в необсаженной части скважины) более рациональным пользоваться приближенными методами.
При промывке скважины в процессе бурения, если диаметр бурильных труб dн не превышает 0,8D , линейные потери рекомендуется определять по формуле Бингама:
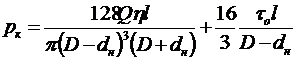. (8.11)
При малых кольцевых зазорах (dн /D >0,8), например, при промывке во время спуска обсадных колонн, допустимо применение формулы для щелевидного канала:
. (8.12)
В разделе 5 было показано (на примере течения ВПЖ в трубах), что потери давления при структурном режиме можно определять и по формуле Дарси-Вейсбаха. Аналогично можно поступить и в случае заколонного пространства. Вначале вычисляют критерии Reк и Senк формулам (8.6) и (8.9). Затем находят Reк*:
, (8.13)
а затем
. (8.14)
Искомые потери давления вычисляют по формуле (8.8).
8.4. Кризис структурного режима движения в заколонном
пространстве.
Вследствие геометрической неопределённости заколонного пространства рекомендуется (в отличие от трубного канала) упрощенная методика определения Qк . При этом критическая скорость vк.кр, соответствующая переходу в турбулентный режим, определяют по формуле:
. (8.15)
Погрешность этой формулы при to > 5 Па относительно невысока. Любопытно отметить, что в соответствии с этой формулой vк.кр не зависит от геометрических размеров канала и структурной вязкости h.
Критический расход Qк.кр вычисляют по формуле:
. (8.16)
8.5. Линейные потери давления при турбулентном движении
вязкопластичной жидкости в заколонном пространстве.
Если Q > Qк.кр наступает турбулентный режим, при котором, как известно, базовой формулой является формула Дарси-Вейсбаха, то все проблемы сводятся к выбору методики определения коэффициента гидравлических сопротивлений lк.
Рекомендуем наиболее распространенную ныне методику вычисления рк. Вначале вычисляют Senк и Reк по формулам (8.9) и (8.6), а затем Re*к по формуле (8.13). Наконец, рк определяют по формуле ВНИИБТ:
. (8.17)
Эта формула рекомендуется для Re*к < 8000. В области квадратичного трения (Re* к > 8000) lк = 0,025.
8.6. Потери давления при ламинарном режиме течения
степенной жидкости в заколонном пространстве.
Методика расчета потерь давления при Q > Qк.кр основана на формулах для трубного пространства (см. раздел 7.2) с последующей модификацией их с использованием понятия "гидравлического радиуса" (замена d в базовых формулах на D-dн ).
Предлагается следующая последовательность расчетных действий.
Вначале оценивают режим движения, сравнивая Q с Qк.кр (методика определения Qк.кр степенной модели дана в разделе 8.7).
Искомые потери давления рассчитывают по формуле:
. (8.18)
Если вместо vк использовать расход Q , то потребуется формула:
. (8.19)
Обратим внимание на то обстоятельство, что способность степенной жидкости разжижаться (n < 1) приводит к "запаздыванию" роста pк при увеличении Q. То же замечательное свойство стенной жидкости мы отмечали, когда получали расчетную формулу для случая течения в трубах.
Наконец, отдадим долг традиции и опишем методику определения рк с помощью формулы Дарси-Вейсбаха. Для этого необходимо вычислить значение "приведенного" Rек.ст степенной жидкости по формулам:
(8.20)
или
, (8.21)
а затем вычислить lк по формуле:
. (8.22)
To обстоятельство, что рк определяют по формуле Дарси-Вейсбаха
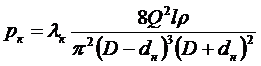, (8.23)
вовсе не означает, что потери давления возрастают в квадрате от расхода Q. Дело в том, что в формуле (8.23) в скрытом виде Q присутствует в знаменателе в соответствии с формулой (8.22). В результате потери давления рк будут теми же, что по формулам (8.18) или (8.19). Характер зависимости рк от Q сохранится, и прирост рк будет отставать от прироста Q, что должно только радовать.
8.7. Кризис ламинарного режима течения степенной жидкости
в заколонном пространстве.
Потери давления начнут стремительно возрастать при переходе в турбулентную область течения. Турбулизация потока в заколонном пространстве начнется при
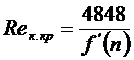, (8.24)
где
. (8.25)
Для определения критического расхода Qк.кр предлагается формула:
. (8.26)
Если Q > Qк.кр , то режим течения турбулентный.
8.8. Потери давления при турбулентном течении степенной
жидкости в заколонном пространстве.
Методика расчета аналогична таковой для случая течения в трубах.
В первую очередь вычисляют Reк.ст по формулам (8.20) и (8.21). Затем – λк по формуле (8.17) с заменой Re*к на Reк.ст :
.
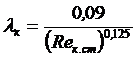Вполне допустимо применение упрощенной методики расчета, аналогичной описанной в разделе 7.3. Вначале вычисляют "последние" потери давления в ламинарной области при Q = Qк.кр:
. (8.27)
Потери давления в области Q > Qк.кр определяют по формуле:
. (8.28)
Последняя формула является сугубо эмпирической.
Дата добавления: 2018-06-27; просмотров: 764; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!