Градиент в криволинейных координатах
Определим выражение для градиента. Будем исходить из общих формул
Найдем величину 
–проекцию вектора градиента функции на направление орта е1 .В данном случае при изменении координаты на 
величина 
получает определенное приращение 
, а величина 
, поэтому
. (150)
Аналогично определяются проекции на орты е2,е3. В итоге находим
(151)
Дивергенция
Найдем выражение для дивергенции в криволинейных координата. Для этого воспользуемся инвариантным определением дивергенции. В качестве области ∆V выбираем элементарный параллелепипед с ребрами 
. Запишем выражение для потока через поверхности, образованные двумя элементарными гранями, перпендикулярными к орту е1:
(152)
Разложим подынтегральное выражение в первом интеграле(152) в ряд в окрестности точки (q1 ,q2 ,q3). Находим
(153)
Далее подставим (153) в первый интеграл(152),после чего находим
(154)
с точностью до величин более высокого порядка малости. Используя теорему о среднем из соотношения (154) получаем
(155)
В формуле (155) частная производная вычисляется в точке (q1,q2*,q3*), где точка (q2*,q3*)∈∆S не определяется теоремой о среднем. Аналогично определяются потоки через оставшиеся пары граней. Выражения для потоков могут быть записаны непосредственно из соображений симметрии. Результирующий поток с точностью до величин более высокого порядка малости определяется по формуле
|
|
|
(156)
Отсюда, используя формулу для элементарного объема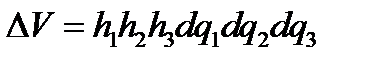 
,находим выражение для дивергенции в точке ( 
)
. (157)
Лапласиан
Получим представление ∆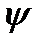 
в криволинейных ортогональных координатах. Для этой цели воспользуемся формулой (23,I.64) и выражением для 
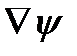(151). Находим
(158)
Ротор
Определим теперь выражение для проекции ротора вектора ана векторе1 или, другими словами , определим величину 
. Построим на координатных линиях q2 и q3 элементарный прямоугольник . Вершины прямоугольника имеют следующие координаты:
A= (q1 ,q2 ,q3), B=(q1 ,q2+∆q2 ,q3),C= (q1 ,q2+∆q2,q3+∆q3),D=(q1 ,q2,q3+∆q3). Длина отрезка АВ равна h2∆q2, BC- h3∆q3, CD- h2∆q2, DA- h3∆q3. Площадь прямоугольника 
По определению проекции ротора в точке А имеем
. (159)
Появление знаков “минус” в правой части (159) обусловлено тем обстоятельством ,что на данных участках направление вектора 
и соответствующего орта противоположны. Например, на участке DA имеем
|
|
|
.
Рассмотрим разность интегралов
Разложим подынтегральное выражение во втором интеграле в ряд по степеням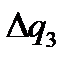 
, ограничиваясь первыми двумя членами разложения. Получаем
Подставив (161) в (160), находим
Далее, воспользовавшись теоремой о среднем, находим
В формуле (163) частная производная взята в некоторой точке на участке АВ. Точно также находим
Этот результат можно предвидеть и без проведения вычислений. Подставляя (163), (164) в формулу (159),получаем
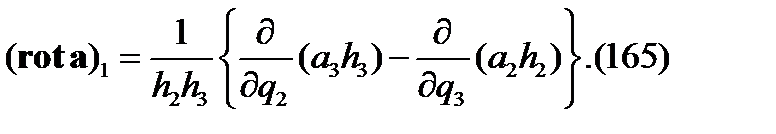
Аналогичные соотношения определяются для других компонент вектора 
.Итоговое соотношение может быть представлено в виде одной формулы
Выражение для 
может быть представлено и в виде определителя третьего порядка
Ниже в примерах решения задач выражение для 
в криволинейных ортогональных координатах найдено другим способом.
Задачи
Примеры решения задач
1 1.Найти выражения для ротора ортов криволинейной ортогональной системы координат.
Решение.
Найдем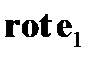 
. Первоначально запишем очевидное равенство, вытекающее из формулы (151), в которой следует положить 
Возьмем 
от обеих частей (168). Используя соотношения (2.65),находим
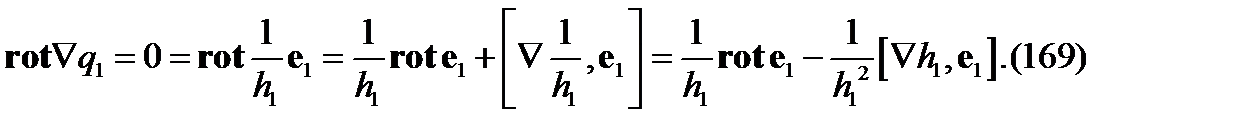
Из формулы (169) далее имеем
Для нахождения 
вместо соотношения (168) следует использовать следующую формулу:
|
|
|
Дальнейший вывод аналогичен проделанному выше. В результате получаем
Это соотношение может быть получено из формулы (170) путем циклической перестановки индексов 1,2,3. Осуществляя циклическую перестановку индексов, определяем следующие последовательности индексов: 3,1,2 и 2,3,1. Для вывода соотношения (172)необходимо воспользоваться второй последовательностью индексов и произвести в формуле (170) следующие замены индексов : 
.С помощью первой последовательности индексов находим далее
12.Найти выражение для ротора вектора в криволинейных ортогональных координатах, используя результаты решения предыдущей задачи.
Решение.
Запишем разложение вектора 
по ортам ортогональной криволинейной системы координат. Имеем
Возьмем ротор от обеих частей (174). Используя формулу векторного анализа (2.86), находим
Вычисляя первое векторное произведение в формуле (175), находим
Для определения других векторных произведений в формуле (175) достаточно произвести циклическую перестановку индексов в соотношении (176). Получаем выражения:
Подставляя (170), (172), (173), (176)-(178) в формулу (175) и осуществляя необходимую группировку слагаемых, определяем
Выражение (179) совпадает с полученным ранее выражением для ротора вектора.
|
|
|
13. Найти производную орта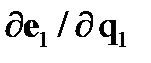 
.
Решение.
Легко видеть, что величина
представляет собой производную от орта 
по направлению того же вектора 
. Далее используем общее соотношение для производной от вектора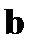 
по направлению вектора 
:
которое было получено ранее (см. (2.22)). В нашем случае соотношение (181) позволяет записать
так как модуль вектора 
равен единице. Соотношение (182) позволяет далее воспользоваться, например, формулой (2.85.). Имеем
Отсюда вытекает
Из соотношений (182), (184) находим
Выражение (185) позволяет далее просто воспользоваться результатами решения первой задачи. Для компактности записи перепишем формулу (170) в виде
Теперь вычисляем векторное произведение:
Наконец, из выражения (185) с помощью формул (186), (187) окончательно получаем
14. Найти выражение 
в криволинейных ортогональных координатах.
Решение.
Ранее были получены следующие формулы векторного анализа (см. (2.85), (2.79)):
Формулы (189) позволяют выразить 
через уже известные выражения для ротора, градиента и дивергенции. Вычитая из второго соотношения (189) первое соотношение,
находим
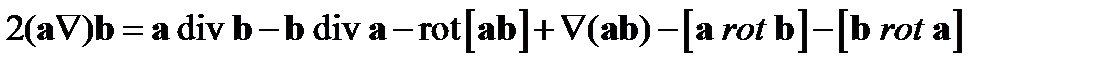. (190)
Далее имеем
(191)
Проведем дифференцирование в формуле (191). После дифференцирования данное выражение будет содержать 52 слагаемых, многие их которых взаимно сокращаются. В итоге находим
(192)
Остальные компоненты вектора 
находятся циклической перестановкой индексов в соотношении (192). Для второй компоненты получаем
(193)
Для третьей компоненты имеем
(194)
15. Найти выражение для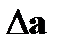 
в криволинейных ортогональных координатах.
Решение
Из формулы векторного анализа (2.71) имеем следующее соотношение
(195)
Так как выражение для градиента, дивергенции и ротора в криволинейных ортогональных координатах нам уже известны, то соотношение (195) позволяет определить выражение для лапласиана вектора. Находим
(196)
Далее аналогично получаем
(197)
Наконец, для третьей компоненты имеем
(198)
Отметим, что в криволинейных ортогональных координатах, вообще говоря, 
.Равенство 
заведомо выполняется только в декартовой системе координат.
16.Записать выражение для 
в цилиндрических координатах.
Решение.
После простых преобразований или непосредственно имеем
; (199) (200) 
; (200)
(201) (201)
(202)
(203)
(204)
(205)
(205)
17. Записать выражения для ∇ 
,div
, rota, ∆ 
, 
в сферических координатах.
Решение
После простых преобразований или непосредственно имеем
(206)
; (207)
(208) 
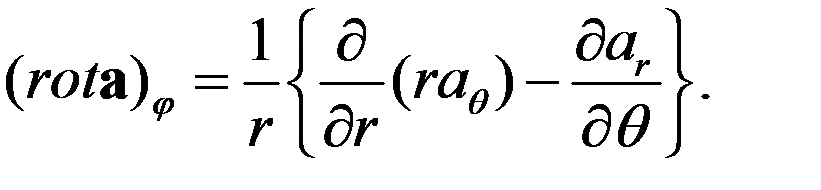
(209)
,
, (210)
.
,
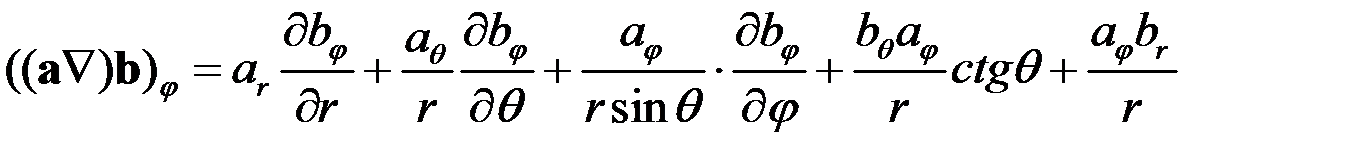, (211)
.
Задача
Найти
.(212)
Далее имеем
(213)
Следовательно,
(214)
Так как выражения для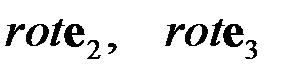 
были получены ранее, то подставляя эти выражения в предыдущую формулу, получим
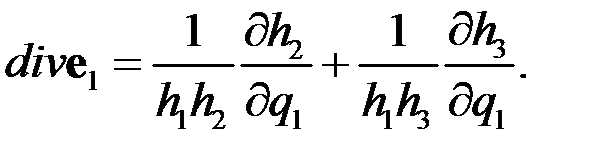(215)
Остальные выражения получаются циклической перестановкой индексов
Имеем
(216)
Наконец
(217)
Найти выражение для дивергенции вектора 
,используя решение предыдущей задачи.
Имеем
Легко видеть, что
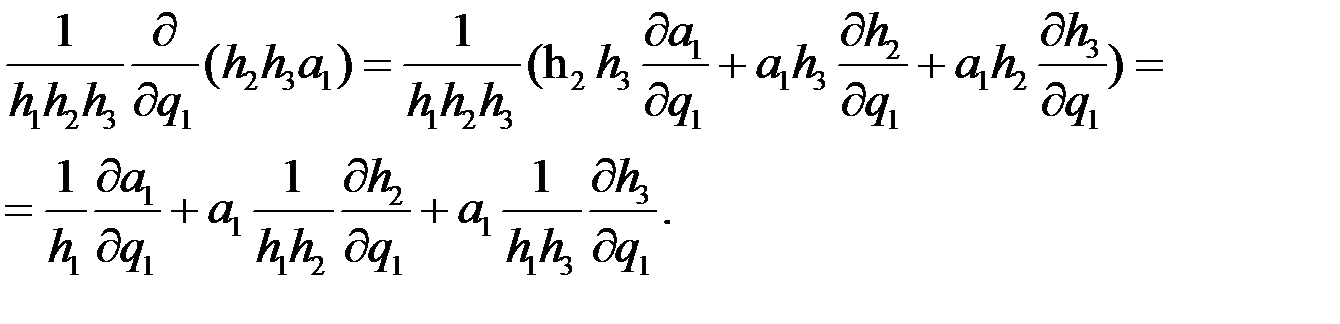(219)
Аналогично преобразуются остальные слагаемые в формуле (218). В итоге получим
(220)
Вопросы к зачету по курсу векторного и тензорного анализа
1. Множества и пространства
2. Векторы. Операции над векторами
3. Скалярное произведение, векторное произведение, смешанное произведение
4. Двойное векторное произведение
5. Системы координат. Правые и левые тройки векторов
6. Формулы преобразования при поворотах системы координат. Операция инверсии. Истинные векторы и псевдовекторы.
7. Эквивалентное определение вектора как свойство при поворотах системы координат
8. Тензор диэлектрической восприимчивости
9. Определение тензора в трехмерном пространстве
10. Истинные тензоры и псевдотензоры
11. Операции сложения и умножения тензоров. Свертка тензора по паре индексов
12. Тензор Леви-Чивиты и его свойства
13. Главная ось тензора
14. Примеры тензорных величин
15. Производная скалярной функции по направлению
16. Градиент скалярной функции и его свойства
17. Линейный интеграл от вектора вдоль кривой. Свойства потенциальных векторных полей
18. Производная векторной функции по направлению
19. Поток вектора через поверхность
20. Дивергенция вектора. Теорема Гаусса-Остроградского
21. Ротор вектора. Теорема Стокса
22. Интегральные соотношения векторного анализа
23. Теорема Грина
24. Основные дифференциальные соотношения векторного анализа
25. Теорема Гаусса-Остроградского для тензора второго ранга
26. Криволинейные координаты. Коэффициенты Ламэ
27. Градиент в криволинейных ортогональных координатах
28. Дивергенция в криволинейных ортогональных координатах
29. Ротор в криволинейных ортогональных координатах
30. Лапласиан в криволинейных ортогональных координатах
31. Сводка основных формул векторного анализа
Дата добавления: 2018-06-27; просмотров: 1578; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!