Свойства антисимметричного тензора второго ранга

 Независимыми являются только три компоненты антисимметричного тензора из девяти, так что антисимметричный тензор второго ранга определяется, как и вектор, тремя величинами, которые обозначим как a₁,a₂,a₃. С использованием этих обозначений

 

.(83)

                                                                                                                          (84)

с учетом того, что соответствующая ему матрица имеет вид

                         (85)

 

 

Ранее мы убедились, что произведение псевдотензора и тензора является псевдотензором, а произведение двух псевдотензоров–истинным тензором. Из того факта, что совокупность величин a_k, умноженная на псевдотензор , дает истинный тензор A_ij, следует, что эта совокупность составляет компоненты некоторого псевдовектора. Таким образом, каждому антисимметричному тензору второгоранга можно поставить в соответствие псевдовектор с компонентами, определяемыми формулами (83). И обратно каждому псевдовектору можно поставить в соответствие антисимметричный тензор с компонентами, выражаемыми теми же формулами (83).

Рассмотрим произведение антисимметричного псевдотензораA и некоторого вектора 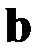. Согласно (83), оно может быть представлено в виде

или

                                                 (86)

Вектор  перпендикулярен как вектору , так и псевдовектору 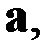 соответствующему антисимметричному тензору A.

Задачи для самостоятельного решения

1) Доказать, что 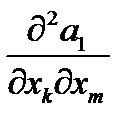есть тензор третьего ранга.

2) Записать тензор ранга  в виде частных производных от компонент вектора .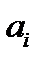

3) Доказать, что есть - тензор второго ранга, а - псевдотензор второго ранга, то

 - псевдоскаляр.

4. Доказать, что сумма диагональных компонент тензора второго ранга является инвариантом.

5. Доказать, что компоненты антисимметричного тензора второго ранга при вращениях преобразуются как компоненты вектора.

6. Доказать тождество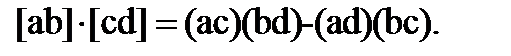

7. Доказать тождество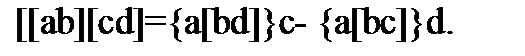

8. Записать в инвариантной векторной форме выражение

9. Доказать, что любой тензор второго ранга можно представить в виде суммы симметричного и антисимметричного тензоров.

10. Доказать тождество (21).

 

Векторный анализ

Производная скалярного поля по направлению

    Выберем в пространстве некоторую точку  и произвольное направление, проведенное из 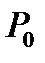и заданное единичным вектором s.Отложим из точки  вектор 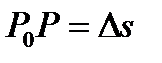 в направлении s.Производной скалярного поля, т.е. скалярной функции  координат, по направлению sназывается следующий предел:

 при    (1)

Если s=e_x, то, очевидно, .Приs=e_y ;приs=e_z .

Градиент скалярного поля

    Рассмотрим точки поля, в которых .Совокупность таких точек образует поверхность, которую называют эквипотенциальной поверхностью или поверхностью уровня. При смещении из точки  на отрезок   по поверхности уровня функция 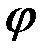 получит приращение

.                                                               (2)

Как обычно, в (2) подразумевается сумма по повторяющимся индексам от 1 до 3. В (2) угадывается скалярное произведение вектора  на вектор . Первый

вектор называется градиентом скаляра :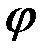

 ,                                                                         (3)  

.

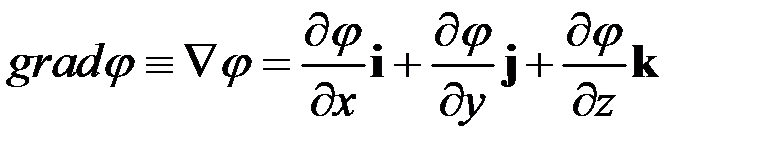Данное определение легко распространить на пространство  измерений. В этом случае число слагаемых в данной формуле будет равно не трём , а .

Гамильтон ввел векторный дифференциальный оператор  , который называют оператором набла или оператором Гамильтона. Он приобретает смысл, будучи примененным к скалярной или векторной функции. Так при символическом умножении  на 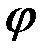 получается градиент 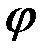. Так как

,                                                                              (4)

и

,

то вектор  в каждой точке поля направлен по нормали к поверхности уровня.

 

Единичный вектор нормали к эквипотенциальной поверхности, направленный в сторону возрастания , обозначим через n.

Легко сопоставить производные по направлению  и . Для этого необходимо рассмотреть две близкие эквипотенциальные поверхности и сравнить формулы предельных переходов (1) для направлений и .В результате находим

                         (5)

Таким образом, производная скаляра по направлению равна проекции вектора градиента на это направление. Направление градиента является направлением наиболее быстрого возрастания скалярной функции .

       Далее имеем

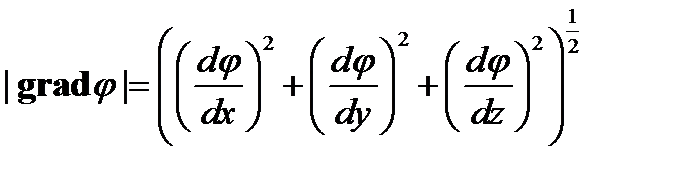. (6)

Очевидно,

Вектор, являющийся градиентом некоторого скаляра , называется потенциальным вектором, а поле такого вектора – потенциальным полем.

Потенциальные векторные поля обладают особыми свойствами, связанными с понятием линейного интеграла вдоль некоторой кривой. Пусть нам задано поле вектора a(r). Возьмем какую-нибудь кривую  соединяющую точки  и . Считаем её ориентированной, т.е. на ней определено положительное направление от точки  к точке . Разобьем её мысленно на малые элементы, которые заменим хордами , и составим сумму скалярных произведений , включающую все упомянутые хорды. Предел этой суммы 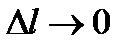при

 

при  и при всех .             (7)

называется линейным(или криволинейнымIIрода) интегралом вектора  вдоль кривой . Этим интегралом, например, выражается работа переменной силы при перемещении материальной точки вдоль некоторой кривой. В общем случае поля, которое нет оснований считать потенциальным, значение этого интеграла зависит от длины и формы кривой (к примеру, работа по передвижению тумбы для награждения победителей среди конькобежцев зависит от того, по льду или снегу, напрямую или в обход будут тащить эту тумбу). Поэтому в отличие от обыкновенного определенного интеграла у линейного интеграла указывают не пределы интегрирования (такого понятия у линейного интеграла нет), а область интегрирования – саму кривую 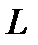. При общеупотребительной краткой записи линейного интеграла подразумевается, что кривая  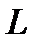каким-либо образом описана. Линейный интеграл вдоль замкнутой кривой называется циркуляцией вектора по этой кривой и обозначается следующим образом:                

 или .

 

Важным свойством потенциального векторного поля является то, что значeние его линейного интеграла не зависит от пути интегрирования, а зависит только от положения начальной и конечной точек интегрирования.

Действительно,

,                                            (8)

т.к. он представляет собой предел суммы приращений потенциала :

Отсюда следует, в частности, что циркуляция потенциального вектора вдоль замкнутого контура равна нулю:

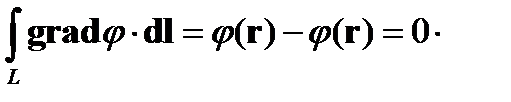
Обратно, если линейный интеграл вектора авдоль всякой замкнутой кривой равен нулю,  вектораявляется потенциальным, т.е. представим градиентом некоторого скаляра. Докажем это утверждение.

       В первую очередь, заметим, что в этом случае интеграл, взятый по некоторому пути  от некоторой точки  до другой точки , будет таким же, как и взятый по любому иному пути  от точки  до точки . Действительно, из этих двух кривых  и  можно образовать замкнутый контур и вычислить вдоль него линейный интеграл, в котором если кривая  проходится от точки  до точки , то кривая  проходится от точки  до точки :

 .

Очевидно, интеграл вдоль кривой  от точки  до точки  будет отличаться от интеграла вдоль этой же кривой от точки  до точки  только знаком, так как при перемене направления в сумму бесконечного числа бесконечно малых слагаемых(в интеграл) будут входить(в обратном порядке) величины , в которых вектор  имеет просто противоположное направление:

.

Таким образом,

Это означает, что

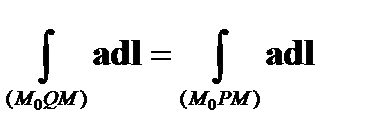,                                                               (9)

т.е. значение интеграла не зависит от кривой и определяется только положениями конечных точек. Следовательно, при фиксированной точке 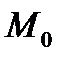 он является функцией r. Обозначим эту функцию как :

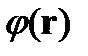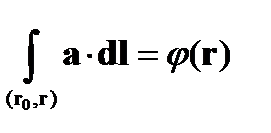                                                                                              (10)

Взяв элементарные приращения обеих частей этого равенства при бесконечно малом перемещении , получим

                                                                                                 (11)

Сравнивая последнее значение с формулой , приходим к равенству

,                                                                                                   (12)

Что и требовалось доказать.

Свойства градиента

Поток вектора

Рассмотрим важное понятие потока вектора через поверхность. В поле вектора a(r)выделим малую плоскую площадку . В пределах малой плоскости векторааможно считать постоянным.

Если задано направление обхода по контуру, ограничивающему площадку , то направление нормали (положительной нормали) nк площадке выбирается так, чтобы нормаль образовала вместе с контуром правовинтовую систему (см. рис 158). Положительную нормаль еще называют внешней нормалью к поверхности . Определим вектор площади соотношениями =n ; dS=ndS.

Потоком вектора a через поверхность называется скалярная величина, определяемая следующим выражением:

.                              (25)

Рассмотрим теперь произвольнуюповерхность S.

Потоком вектора  через  называется

 =                   (26)

Здесь  - проекция вектора  на положительную нормаль к площадке  ,  - вектор элементарной площадки, его модуль равен величине площадки , а направление совпадает с направлением положительной нормали к площадке. При вычислении потока через замкнутую поверхность положительной считается внешняя нормаль.

Окружим точку  поля замкнутой поверхностью 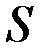 . Величину

                      (27)

наз. дивергенцией векторного поля в точке .

Найдем выражение для дивергенции в декартовой системе координат. Возьмем в окрестности точки  объем в виде прямоугольного параллелепипеда с гранями, перпендикулярными к координатным осям. Найдем поток вектора через грани 1 и 2, перпендикулярные к оси x. Внешняя нормаль к грани 1 совпадает по направлению с осью x. Поэтому для этой грани  . Индекс 1 указывает, что значение  берется в точке, лежащей на грани 1. Внешняя нормаль к грани 2 противоположна по направлению оси x. Поэтому для неё . Индекс 2 указывает, что значение  берется в точке, лежащей на грани 2. Суммарный поток через грани 1 и 2 равен

 ,                  (28)

где  ,  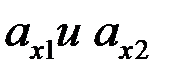берутся для точек граней 1 и 2 с одинаковыми  . Интеграл, стоящий справа, берется по поверхности   любой из граней 1 и 2.

Разложим  в ряд в окрестности точки :

 

 (29)

Здесь  - величина более высокого порядка малости, чем разности

 , т.е. величина, убывающая быстрее, чем линейные размеры параллелепипеда. 

  Положив в выражении (29)  , найдём  . Положив в выражении (4)  , найдём 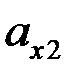 . Вычтя эти значения друг из друга, получим

 ,

где  - величина, убывающая быстрее, чем линейные размеры объема. Подставив найденное значение в (29), получим

Далее имеем

 .

Поэтому

 ,

где  - величина более высокого порядка малости, чем  . Аналогично получаем  

, .

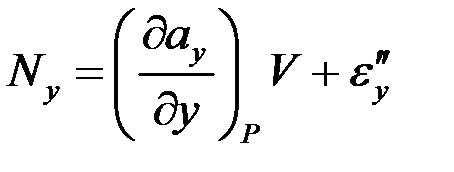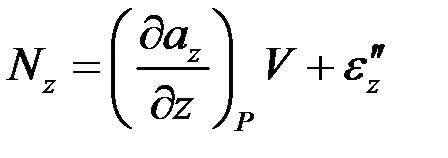 Сложив вместе найденные потоки, получим полный поток через поверхность параллелепипеда. Разделив этот поток на и сделав предельный переход  , придем к формуле

 .                            (30)                                               

Мы учли, что при предельном переходе величины  обращаются в нуль.

 Определение дивергенции также можно распространить на пространство  измерений. В этом случае под элементом объема следует понимать . Интеграл надо брать по гиперповерхности размерности . Элемент гиперповерхности, перпендикулярный к оси 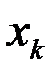, будет равен  . В пространстве четырёх измерений гиперповерхностью будет обычный трёхмерный объём. 

Возьмем в поле вектора  конечный объём  , ограниченный поверхностью . Разобьём этот объём на элементарные объёмы . Согласно (27 ) для потока 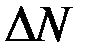  через поверхность такого объёма можно записать

 .

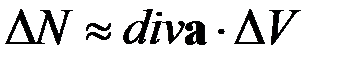Сложим эти выражения для всех элементарных объёмов. При суммировании 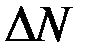потоки через грани, разделяющие два соседних объёма, взаимно уничтожаются. Для смежных участков потоки отличаются знаками, так как внешние нормали  для них имеют противоположные направления. Некомпенсированными останутся только потоки через участки внешней поверхности 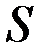 , так что в сумме получится поток вектора  через эту поверхность. Сумма справа в пределе при  превратится в интеграл по всему объёму. Приближенное равенство в пределе перейдет в строгое равенство. В итоге получим

 .                                                     ( 31 )

Полученное соотношение носит название теоремы Гаусса-Остроградского:

Поток вектора через замкнутую поверхность равен интегралу от дивергенции этого вектора по объёму, ограниченному этой поверхностью.

Из этого соотношения легко установить двумерную форму теоремы Гаусса-Остроградского. Для этой цели применим (31 ) к тонкому диску с толщиной 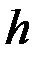 . Пусть основание диска ограничено контуром  . Очевидно

 .

Элемент площади боковой поверхности равен  , где  - элемент длины контура . Переходя к пределу в (31 ) при  , находим двумерную форму теоремы Гаусса-Остроградского

.                                                    (32)

В данной формуле  - проекция вектора  на направление внешней нормали ккривой . При записи данного соотношения мы учли, что при  потоки вектора  через верхнее и нижнее основания диска взаимно компенсируются.

 

Ротор вектора

Преобразуем циркуляцию вектора  вдоль кривой Lв интеграл по по­верхности, опирающейся на данную кривую. Первоначально рассмотрим пло­ский контур. Пусть единичный вектор  направлен по касательной к кривой L в соответствии с ориентацией данной кривой. Проведем вектор нормали  к плоскому контуру так, чтобы направления , ,  образовывали правовинтовуюсистему. Введем вспомогательный вектор  и применим к нему теорему Гаусса-Остроградского в двумерном случае. Имеем

 

(33)

 

 

Рассмотрим совокупность трех величин

.                   (34)

 

Легко непосредственно проверить, что эти величины можно представить в виде

      .

(35)

Так как в соотношении (35) в правой части указано произведение тензоров с последующей сверткой по двум индексам, то, следовательно, совокупность трех величин (34), (35) образует вектор. Этот вектор обозначают следующим образом:

. (36)

Ротор вектора в русской литературе еще называют вихрем вектора. В англоязычной литературе вместо rot a нередко используется обозначение curl a. Легко видеть, что выражение для ротора вектора можно представить в виде векторного произведения вектора-оператора  и вектора и соответственно в виде следующего определителя:

          .                        (37)

 

В соответствии с формулами (35), (37), очевидно, имеем

.

(38)

Теперь, в соответствии с формулой (37), получаем

 .                        (39)

Кроме того имеем

         .                                       (40)

Поэтому из соотношения (36) находим

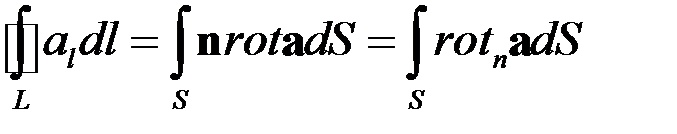      .                                                      (41)

               

Соотношение (41) и выражает собой теорему Стокса, доказанную пока для случая плоского контура. Рассмотрим теперь конструкцию доказательства в общем случае.

 

Формула Стокса

    Теперь рассмотрим в поле вектораапроизвольную регулярную поверхность S, ограниченную ориентированным контуром L (контур не является обязательно плоским). Разобьем эту поверхность на малые элементы, которые можно считать плоскими. Ориентация контуров малых элементов выбирается первоначально вблизи контура L в соответствии с его ориентацией и далее продолжается «по непрерывности». Для каждого из таких малых элементов имеем

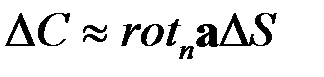 ,                                                                           (46)

где ΔC — величина циркуляции. Сложим выражения (46) для всех таких элементов. При этом, очевидно, циркуляции, взятые вдоль границ раздела малых соседних элементов, взаимно уничтожаются вследствие противоположной ориентации смежных контуров. Некомпенсированными останутся только величины  для участков, совпадающих с контуром L. Эти величины дадут в совокупности циркуляцию вектора aпо контуру L. Сумма же от слагаемых в правой части (46) в пределе при всех  становится интегралом от  по поверхности S. Приближенное равенство, получающееся в результате сложения выражений (46), в пределе переходит в точное равенство. Таким образом, находим

                                     (47)

В отличие от соотношения (45) формула (47) выполняется в общем случае для произвольного регулярного контура и произвольной регулярной поверхности, натянутой на данный контур.

    Итак, выполняется следующая теорема(теорема Стокса): циркуляция произвольного  вектора по регулярной замкнутой кривой равна потоку ротора этого вектора через произвольнуюрегулярную поверхность, опирающуюся на данную кривую.

Мы по-прежнему полагали, что однозначная функция a(r)непрерывна и имеет непрерывные частные производные в некоторой области, в которой лежит поверхность S. Ориентация элементарных площадок dSсогласуется о ориентацией контура L по правилу правого буравчика. Такая ориентация первоначально производится  у края поверхности и далее продолжается по непрерывности.

---

Дата добавления: 2018-06-27; просмотров: 1753; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!