Смешанное произведение векторов
Смешанным произведением векторов a,b,cназывается скалярная величина
. (6)
представляющая собой скалярное произведение вектора а на вектор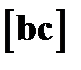 
.Действительно,
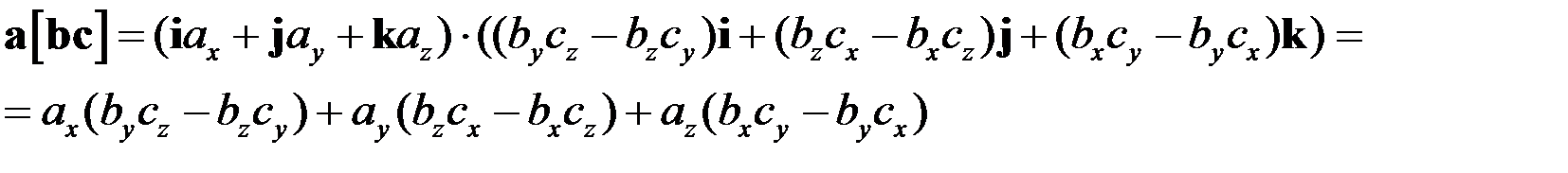
Выражение в правой части последнего соотношения и представляет собой определитель (6).
Из известного свойства определителя ( если в квадратной матрице поменять местами любые две строки, то определитель матрицы только изменяет знак) вытекают следующие равенства
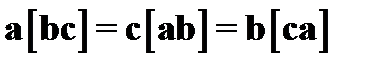. (7)
Другими словами, смешанное произведение допускает циклическую перестановку сомножителей. Смешанное произведение обозначают еще так
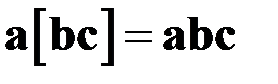. (8)
| a |
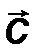на это векторное произведение дает высоту параллелепипеда, следовательно, модуль смешанного произведения равен объему этого параллелепипеда. Смешанное произведение положительно, если вектор 
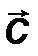составляет острый угол с векторным произведением, как на рисунке, в противном случае отрицательно.
Направление векторного произведения меняется на противоположное при переходе от правой системы координат к левой. Одновременно меняется знак смешанного произведения. Поэтому смешанное произведение не является истинным скаляром. Такие геометрические объекты называются псевдоскалярами (псевдотензорами валентности ноль).
|
|
|
Формулы преобразования при поворотах системы координат
Рассмотрим две правые декартовы системы координат с общим началом (нештрихованную и штрихованную). Для радиус-вектора имеем
,
.
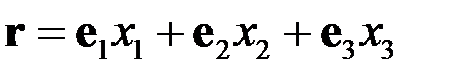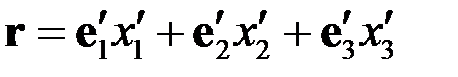Умножим обе части первого соотношения скалярно на 
. Получим
.
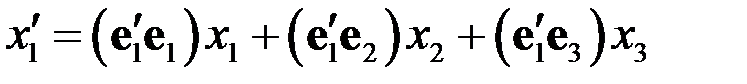Далее имеем
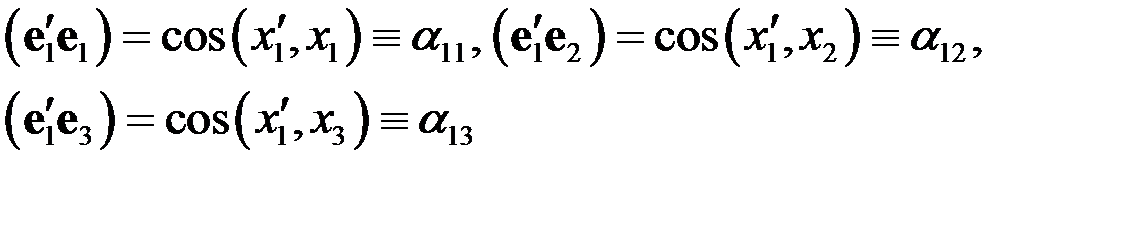
Отсюда имеем
.
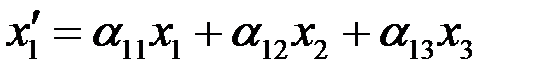Далее умножаем на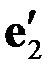 
, потом на 
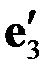. В итоге получим
.
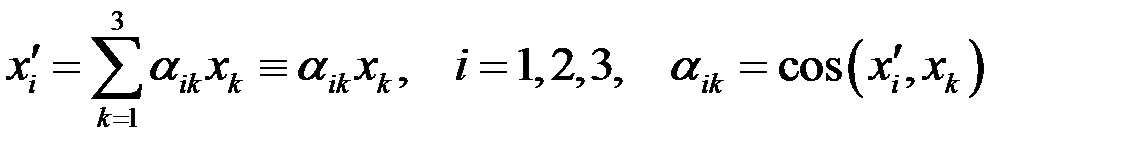Здесь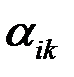 
- косинус угла между 
-той осью штрихованной системы координат и k–той осью исходной (нештрихованной) системы координат. Индексi в данном соотношении наз. свободным, а индекс k наз. немым. Выбор обозначений немых индексов произволен с тем ограничением, что они не должны совпадать со свободными индексами или с немыми индексами других сумм. Докажем, что коэффициенты преобразования удовлетворяют соотношению
.
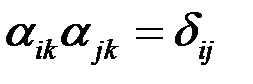Имеем
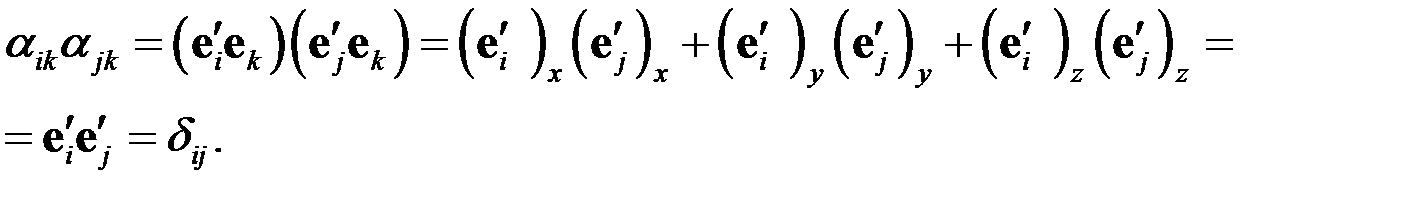
Аналогично доказывается соотношение
.
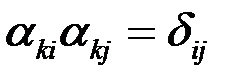Кроме операции поворота системы координат рассматривают операцию инверсии системы координат (операцию зеркального отражения):
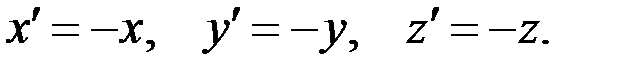
При инверсии координатных осей правая система координат переходит в левую.
|
|
|
Тензоры
Сначала дадим другое эквивалентное определение вектора, которое позволяет распространить понятие вектора на n-мерное пространство и внести понятие тензора. Мы доказали, что при поворотах системы координат декартовы координаты преобразуются по формулам
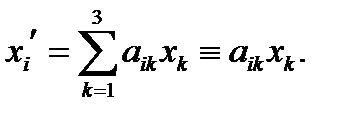. (9)
Еще раз отметим следующее.
Здесь использовано правило Эйнштейна суммирования по повторяющимся индексам. Индекс i в данном соотношении называется свободным, а индекс k , по которому производится суммирование , - немой. Выбор обозначения немых индексов произволен с тем ограничением, что он не должен совпадать со свободными индексами или с немыми индексами других сумм. Например, в формуле(1) вместо индекса k можно использовать любой другой, кроме индекса i . Скалярное произведение векторов aи bпо правилу Эйнштейна может быть представлено в виде
.
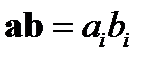Обычно в подобный формулах будем предполагать, что свободный индекс может принимать значения 1,2,3. Общее правило индексных обозначений в произвольных тензорных соотношениях будет дано ниже.
В формуле (1) коэффициенты преобразования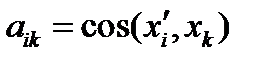 
представляют собой косинусы углов между i-ой осью повернутой системы координат и k-ой осью исходной системы. Коэффициенты преобразования удовлетворяют следующим соотношениям
|
|
|
, 
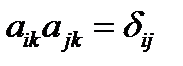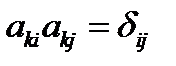. (10)
Операция инверсии системы координат(операция зеркального отражения) заключается в изменении знаков координат
, 
, 
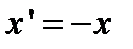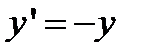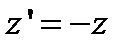. (11)
Дата добавления: 2018-06-27; просмотров: 330; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!