Умножение вектора на скаляр. Орт

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ и МАГНИТНЫХ ЯВЛЕНИЙ

Векторный и тензорный анализ

В данномкурсе сжато излагаются основные сведения из векторного и тензорного анализа, которые в дальнейшем используются при рассмотрении электрических и магнитных явлений. Как известно, все физические законы обладают инвариантностью относительно перемещений и поворотов координатных осей. Такие свойства симметрии физических законов требуют применения адекватных математических объектов – векторов и тензоров.

Литература:

1. А.М. Сагалаков, В.В. Чертищев Основы векторного и тензорного анализа. Барнаул, 2005, 176 с.

2. А.М. Сагалаков, В.В. Чертищев Векторный анализ и начала тензорного анализа. Барнаул, 2012, 171 с.

3. А.М. Сагалаков, В.В. Чертищев Векторный анализ и начала тензорного анализа для физиков. Барнаул, 2014, 172 с.

Введение. Множества и пространства

Под множеством понимают объединение в единое целое определенных вполне различаемых предметов (объектов), которые при этом называются элементами образуемого ими множества.

Обозначения

aÎM                                   a–элемент множества M.

Æ                                        пустое множество.

{x|H(x)} или {x: H(x)}    множество всех объектов, обладающих свойством H(x).

A₁®A₂                              еслиA₁, тоA₂.

A₁«A₂                              A₁эквивалентно A₂.

Символическая запись      Кванторыобщности

"aÎM                                 для всех aÎM;

$aÎM                                 существует aÎM;

Множество M₁ содержится (операция включения) в множестве M₂: M₁ÍM₂ (или M₂ÊM₁), когда выполняется условие: если aÎM₁, то aÎM₂:

M₁ÍM₂                                                      aÎM₁®aÎM₂;

M₂ÊM₁                                                      aÎM₁®aÎM₂;

Если M₁ÍM₂, то множество M₁ называется подмножеством множества M₂; если к тому же M₁¹M₂, то M₁ называют собственным подмножеством множества M₂ и обозначают M₁ÌM₂.

Условие равенства множеств M₁ и M₂можно записать в виде

M₁=M₂«"x{xÎM₁«xÎM₂}

ОбъединениеM₁UM₂двух множеств M₁ и M₂ есть множество всех элементов, принадлежащих хотя бы одному из этих множеств.Пересечение M₁IM₂ двух множеств M₁ иM₂ есть множество всех элементов, принадлежащих как M₁, так иM₂. Если таких элементов нет, то M₁IM₂=Æ–пустое множество.

Топологией в некотором множестве X называется любая система t его подмножеств G, удовлетворяющих двум требованиям:

1. Само множество X и пустое множество Æ принадлежатt.

2. Сумма 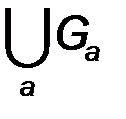 любого (конечного или бесконечного) и пересечение конечного  множеств из t принадлежат t.

Множество X с заданной в нём топологией, т. е. пара (X, t), называется топологическим пространством. Топологическое пространство может рассматриваться и как некоторая совокупность точек с определённой топологией, которой определяется понятие точек, близких друг к другу. Иными словами, топология позволяет определить окрестность точки многообразия, то есть совокупность точек, близких к данной; топологическое многообразие–это множество точек, для которых определено понятие близости. Если можно устанавливать взаимно однозначное соответствие между этими точками и точками евклидова (см. ниже) пространства таким образом, что в области наложения двух таких отображений они выражаются друг через друга непрерывным и дифференцируемым образом, то такое топологическое пространство называют дифференцируемым многообразием.

Поскольку топологическое многообразие не представляет большого интереса для физики, то чтобы конкретизировать его, необходимо приписать ему определенную геометрическую структуру. Тогда можно попытаться установить соответствие между геометрической структурой и теми физическими величинами, которые мы хотим описать. Как мы увидим, существуют геометрические величины, называемые векторами и тензорами, которые могут быть сопоставлены реальным физическим объектам. Так, например, с электромагнитным полем обычно связывают некоторый антисимметричный тензор.

Множество M объектов (точек) x, y, z, … называетсяметрическим пространством, если для каждой упорядоченной пары точек x, y из Mопределено действительное число r(x, y) (расстояние между x и y, метрика) такое, что

1) r(x, y)=0 в том и только в том случае, когда x=y;

2) ( x, y)= (y, x);

3) r(x, y)£r(x, z)+r(z, y) для любых x, y, z из C (неравенство треугольника).

Множество M называется линейным (или векторным, или аффинным) пространством, если в нем определены операции сложения и умножения на действительные числа, не выводящие за пределы M и удовлетворяющие условиям (где a иb–действительные числа)

1) ассоциативности сложения;

2) коммутативности сложения;

3) существует нулевой элемент ÆÎM;

4) 0×x=Æ для всех xÎM;

5) (a+b)x=ax+bx;

6) a(x+y)=ax+ay;

7) a(bx)=(ab)x;

8) 1×x=x.

Линейное пространство называется конечномерным, если в нем можно найти конечную максимальную линейно независимую систему векторов; всякая такая система векторов (e₁, e₂,…, e_n) будет называться базой этого линейного пространства.Вектору x однозначно соответствует строка (x₁, x₂,…, x_n) коэффициентов (координат в данной базе) его выражения через базу x₁e₁+x₂e₂+… +x_ne_n.

Аффинным преобразованием называется преобразование координат, определяемое формулой гдеa_k^i¢, b^i¢–вещественные постоянные,kиi¢–соответственно нижний и верхний индексы, а определитель ||a_k^i¢|| отличен от нуля.

Множество M называется линейным нормированным пространством, если оно линейно и каждому элементу xÎMпоставлено в соответствие действительное число ||x||, называемое нормойx и удовлетворяющее аксиомам нормы:

1. ||x||³0, причем ||x||=0 тогда и только тогда, когда x=Æ, то есть x является нулевым элементом в M.

2. ||ax||=|a|×||x|| для любого действительного a.

3. ||x+y||£||x||+||y|| для всех x, yÎM.

Скалярным произведением в действительном линейном пространстве R называется действительная функция (x,y), определённая для каждой пары элементов x,yÎR и удовлетворяющая следующим условиям:

1) (x, y)=(y, x),

2) (x₁+x₂, y)=(x₁, y)+(x₂, y),

3) (lx, y)=l(x, y),

4) (x, x)³0, причём (x, x)=0 только при  Ø.

Линейное нормированное пространство с фиксированным в нём скалярным произведением и нормой ||x||  называется евклидовым пространством.

 

Векторы и тензоры

Векторы

       Векторами в трехмерном пространстве называются направленные отрезки, которые складываются геометрически (по правилу параллелограмма). Длина отрезка, изображающего вектор, называется абсолютной величиной вектора или его модулем. Можно еще сказать, что вектор задается упорядоченной парой точек.

Направление вектора обозначают стрелкой. Записывают

 .

Здесь  -начало вектора (первая точка отрезка),  - конец вектора (вторая точка отрезка). Векторы обозначают буквами жирного шрифта или отмечают стрелками сверху, или чертой сверху. Нулевым вектором называется вектор, у которого начало и конец совпадают. Направление нулевого вектора произвольно, а модуль его равен нулю. Его нередко обозначают через 0, но при этом необходимо помнить, что это не число 0.

Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых.

Вектор, длина которого равна 1, называется единичным вектором. Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора .

Умножение вектора на скаляр. Орт

Умножение вектора 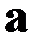 на скаляр l>0 по определению дает вектор  имеющий то же направление, что и вектор 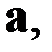 но величину в lраз большую (в 1/l меньшую, если l<1). Умножение на скаляр l<0 дает вектор  имеющий направление, противоположное вектору  и величину в |l| раз большую величины вектора  В обоих случаях векторы  параллельны друг другу. Такие векторы мы назваликоллинеарными. Важен случай, когда один из коллинеарных векторов имеет величину, равную единице (не имея размерности). Такие векторы называют единичными векторами или ортами. Орты будем обозначать буквой Любойпараллельный орту вектор  можно представить в виде

и наоборот, орт для направления вектора можно определить как

                                                                    (1)

 

Cложение векторов

Сложение векторов осуществляют с помощью правила параллелограмма или правила треугольника: чтобы получить вектор  представляющий собой сумму двух векторов  по правилу треугольника надо от произвольной точки A пространства отложить вектор  к концу его приложить начало вектора  и соединить точку A с концом C вектора  тогда  по величине и направлению представит вектор  Из правила параллелограмма очевидно, что сложение коммутативно: Сложение трех и более векторов ассоциативно, то есть складывать их можно в произвольной последовательности:

         Другие свойства:

,

,

, ассоциативность умножения вектора на число

, дистрибутивность по отношению к сложению чисел

, дистрибутивность по отношению к сложению векторов

 .

Определение разности двух векторов

.

 

Базис. Разложение по базису.

Базисом на плоскости наз. два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.

Базисом в пространстве наз. три некомпланарных вектора, взятые в определенном порядке.

Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам. Чаще всего рассматривается разложение вектора по базису.

Пусть  - базис в пространстве и

 - разложение по базису.

 Числа  наз. компонентами вектора  в данном базисе.

Пишут

или .

Теор. Каждый вектор может быть разложен по базису в пространстве. Такое разложение единственно.

Равные векторы имеют одинаковые компоненты.

Теор. При умножении вектора на число все его компоненты умножаются на это число.

Теор. При сложении векторов складываются их соответствующие компоненты.

 

Системы координат

Декартовой системой координат в пространстве называют совокупность точки – начала координат- и базиса.

  Прямые, проходящие через начало координат в направлении базисных векторов, наз.

осями координат. Первая ось – ось абсцисс, вторая – ось ординат, третья – ось аппликат.

Компоненты радиус-вектора точки М по отношению к началу координат наз. координатами точки М в рассматриваемой системе координат.

Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единице.

Декартова система координат, базис которой ортонормирован, наз. декартовой прямоугольной системой координат. Орты в ней обозначаются

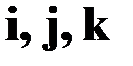 или  или .

Ортогональные базисные тройки разделяются на два класса, носящих название правовинтовых и левовинтовых троек. Тройки одного и того же класса могут быть приведены в совпадение вращением. Тройки же правовинтовые переходят в тройки левовинтовые путем зеркального отображения, т.е. путем обращения направления всех трех векторов тройки. Важно отметить, что не существует инвариантного геометрического определения этих двух классов троек. Чтобы определить правую тройку необходимо конкретно указать какую-либо тройку этого класса.

Принято считать ортогональную тройку правой, если с конца третьего вектора тройки кратчайший поворот от первого вектора тройки ко второму виден совершающимся против часовой стрелки. В противном случае тройка называется левой. 

 

---

Дата добавления: 2018-06-27; просмотров: 573; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!