Задачи, примеры, доказательства некоторых соотношений

⇐ ПредыдущаяСтр 6 из 13Следующая ⇒

1.Доказать тождество

. (38)

Используя определение векторного произведения (30) и определение скалярного произведения (28), имеем

(39)

2.Доказать, что девятикомпонентная величина , где - компоненты векторов, является тензором второго ранга.

Решение

При поворотах системы координат имеем

Поэтому

(40)

Если векторы а и b являются истинными, то при инверсии их компоненты изменяют знак. Поэтому компоненты тензора при инверсии не изменяются. Следовательно, в соответствии с формулой (16), данный тензор является истинным. Если же один из этих векторов является псевдовектором, то и тензор будет псевдотензором. Если оба вектора являются псевдовекторами, то рассматриваемый тензор будет, очевидно, истинным тензором.

Обратим внимание на разные обозначения немых индексов в первых двух соотношениях формулы (30). Использование разных обозначений немых индексов является общим правилом при решении различных задач. Кроме того, обозначения немых индексов не должны, очевидно, совпадать с обозначениями свободных индексов.

3. Доказать, что коэффициенты преобразования 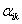удовлетворяют следующим соотношениям (см. формулу (10)): .

Решение

По определению коэффициентов преобразования имеем

Поэтому находим

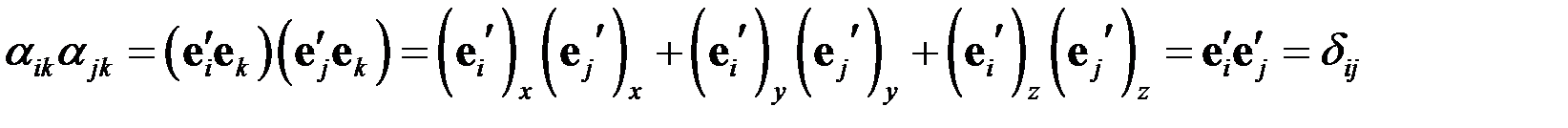
4.Доказать, что совокупность компонент символа Кронекера , заданных одинаково во всех системах координат, образует тензор второго ранга (единичный тензор).

Решение

Используя свойство символа Кронекера, имеем

Таким образом, совокупность девяти величин , заданных указанным выше способом, действительно преобразуется при поворотах системы координат как тензор второго ранга. Так как при отражениях истинный тензор второго ранга не имеет знака , то это означает, что тензор является истинным тензором.

5. Доказать, что совокупность частных производных образует тензор второго ранга ( – компоненты вектора, являющиеся функциями координат).

Решение

Имеем

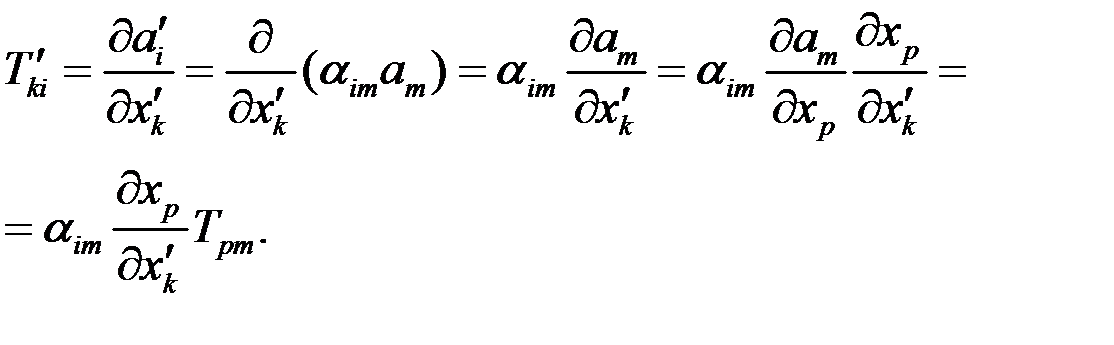(41)

В формуле (31) учтено, что каждая «нештрихованная» переменная х зависит от «штрихованных» переменных . Использованы разные обозначения для немых индексов в соответствии с рекомендацией, данной при решении задачи 2.

Теперь остается записать формулы обратного преобразования координат при поворотах координатной системы. Для этой цели просто отметим, что исходная система координат и повернутая система координат эквивалентны. Поэтому формулы преобразования будут иметь вид

, (42)

где – косинус угла между р-той осью «нештрихованной» системы координат (которая здесь играет роль повернутой системы координат) и n-той осью «штрихованной» системы координат. Но косинус угла между р-той осью «нештрихованной» системы координат и n-той осью «штрихованной» системой координат мы ранее обозначили через . Поэтому формула (42) принимает вид

(43)

Соотношение (43) может быть получено и из формулы прямого преобразования с помощью второго соотношения (10). Имеем

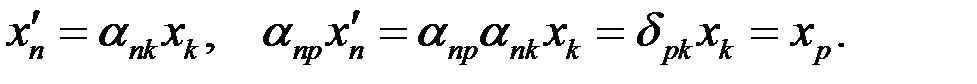(44)

Теперь вычисляем частные производные в формуле (31). Находим

(45)

Подставляя (35) в (31), получаем

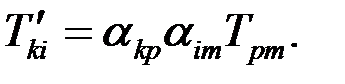(46)

Соотношение (46) соответствует определению тензора второго ранга. Если вектор истинный, то при инверсии координат совокупность частных производных не изменяет знак, следовательно, в этом случае тензор является истинным. Если же является псевдовектором, .то тензор становится псевдотензором.

6. Доказать, что .

Решение
Используя свойства дистрибутивности и соотношение (19), находим.

(47)

Изменяя обозначение немого индекса на и рассматривая компоненту векторного произведения, находим

. (48)

В формуле (48) использованы очевидные соотношения

при . (49)

Соотношение (48), очевидно, совпадает с искомым, так как отличается от него лишь обозначением немых индексов.

7. Установить соотношение(4).

Решение

Для решения достаточно воспользоваться соотношением (47), правую часть которого следует просто расписать, подставить значение величин и сопоставить полученное выражение с определителем в соотношении (4).

8. Доказать справедливость формулы «бац минус цаб».

Решение

Для доказательства этого соотношения запишем -тую компоненту двойного векторного произведения с использованием псевдотензоров , а также воспользуемся очевидными свойствами символа Кронекера. Имеем

(50)

Три соотношения (50), очевидно, эквивалентны одному векторному равенству

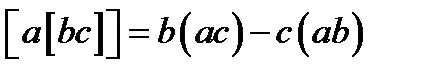(51)

которое и выражает собой правило «бац минус цаб».

9. Доказать, что совокупность величин , одинаково определенных во всех системах координат, действительно образует псевдотензор третьего ранга.

Решение

Требуется доказать, что

(52)

Докажем равенство (52) для компоненты . Имеем

(53)

Далее в соотношение (43) необходимо подставить конкретные значения . Очевидно, имеем

(54)

Подставив (44) в (43), убеждаемся в том, что
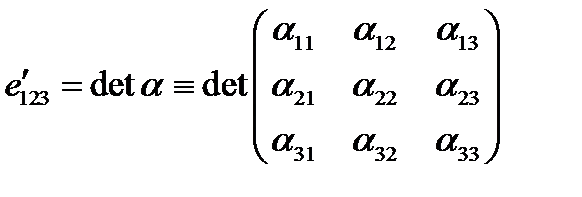.(55)

Далее для нахождения определителя запишем соотношения (10) в матричной форме. Очевидно, имеем

.(56)

Здесь - транспонированная матрица , а - единичная матрица. Используя теорему об определителе произведения матриц, находим.

(57)

Так как определитель транспонированной матрицы совпадает с определителем исходной матрицы, то далее из соотношения (47) находим.

, .(58)

Значение не подходит по смыслу, в чем легко убедиться, рассмотрев, в частности, тождественное преобразование с матрицей

.(59)

Определитель такого преобразования, очевидно, равен . Итак, мы доказали, что

.(60)

Далее рассмотрим преобразование

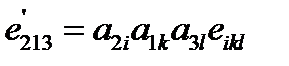.(61)

Имеем

.(62)

В соотношении (52) использовалась замена обозначений немых индексов: индекс заменен индексом , а индекс заменен индексом . Кроме того, было учтено, что

Далее подобные манипуляции производятся для остальных ненулевых компонент, которые приводят к аналогичным результатом.

Допустим теперь, что у величины какие-либо два индекса равны. Рассмотрим, например, преобразование

.(63)

Справедливость соотношения (63) становится очевидной, если в него подставить значения компонент тензора (см.(54)).

Аналогично рассматриваются преобразования остальных компонент, которые приводят к подобным результатом.

Таким образом, при поворотах системы координат величина преобразуется как тензор третьего ранга.

По определению компоненты тензора одинаковы во всех декартовых систем координат. Поэтому при отражениях тензор не изменяется. Истинный же тензор третьего ранга при инверсии координат должен изменять знак. Следовательно, тензор является псевдотензором третьего ранга.

10. Доказать, что если тензор - симметричный, а тензор - антисимметричный, то

.(64)

Решение

В силу условия задачи

Поэтому

11. Доказать тождество

.(65)

Решение

Рассмотрим определитель

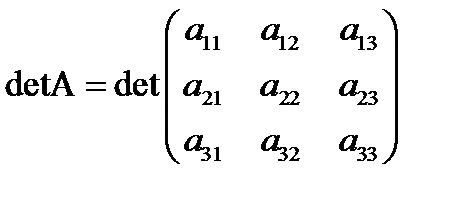. (66)

Как известно, перестановка строк или столбцов приводит к изменению знака определителя. В выражении (66) строки определителя расположены а порядке 1,2,3. При четной перестановки строк знак определителя не изменяется, а при нечетной перестановке определитель изменяет знак. Такому поведению знака определителя соответствуют изменения знака величины 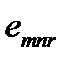при перестановке индексов у компонент тензора . Поэтому можно записать