Инвариантное определение ротора
Из соотношения (45)(или (47)) вытекает инвариантное (не зависящее от системы координат) определение проекции ротора.
Рассмотрим произвольную точку M и произвольную малую площадку 
, на которой лежит точка M. Выберем нормаль n к данной площадке. Тогда, очевидно, будем иметь
. (48)
Легко пояснить геометрический смысл и название ротора. Для этой цели рассматривают вращение твердого тела с угловой скоростью ω. Оказывается, что ротор скорости vодинаков во всех точках тела, причем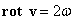 
.Вообще 
в тех точках тела, которые принадлежат его участкам, участвующим во вращательном движении.
Другие интегральные соотношения векторного анализа
Рассмотрим теперь другие важные интегральные соотношения векторного анализа.
Пусть скалярная функция φ в рассматриваемой области имеет конечные частные производные по всем координатам. Преобразуем линейный интеграл 
(этот интеграл, очевидно, является вектором) по произвольному замкнутому контуру в интеграл по поверхности, опирающийся на данный контур. Для того чтобы в дальнейшем воспользоваться одной из теорем векторного анализа (теоремой Стокса), умножим данный интеграл на произвольный постоянный вектор c. Данный прием используется при выводе некоторых других соотношений векторного анализа. Находим
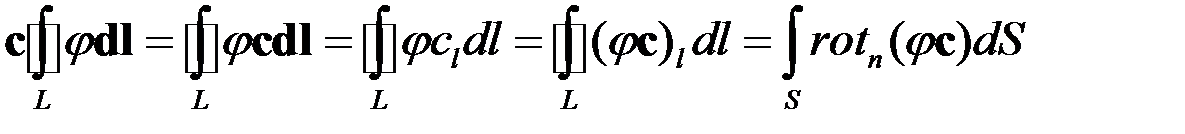
(49)
Далее имеем
|
|
|
(50)
Поэтому соотношение (49) продолжается в виде
(51)
В формуле (51) вектор n – нормаль к поверхности S, которая образует правовинтовую систему с ориентированным контуромL. Используя свойство циклической перестановки сомножителей в смешанном произведении, имеем
(52)
Подставляя (52) в (51), получаем
(53)
Так как вектор с произвольный, то из соотношения (53) вытекает
(54)
Формула (54) и представляет собой искомое соотношение.
Преобразуем интеграл от ротора произвольного вектора по произвольному объему в интеграл по замкнутой поверхности, ограничивающей данный объем. Для того чтобы воспользоваться теоремой Гаусса-Остроградского, умножим интеграл на произвольный постоянный вектор 
. Находим
(55)
В преобразованиях (55) использовано соотношение div[ac]=crota которое уже фактически было установлено при доказательстве теоремы Стокса в плоском случае (роль n здесь играет вектор c). Итак, установлено, что
(56)
Так как постоянный вектор с произволен, то из соотношения (56) вытекает окончательное соотношения
|
|
|
(57)
Теорема Грина
Важным интегральным соотношением, которое широко используется в физике, является теорема Грина. Эта теорема по существу является следствием теоремы Гаусса-Остроградского. Положим в соотношении Гаусса-Остроградского 
Находим
(58)
Здесь “ 
” – оператор Лапласа. Отметим, что поскольку дивергенции скаляра не существует, заключение в скобки “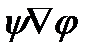 
” не является необходимостью, что и было учтено при за записи div ( 
).
Выполняется
Далее имеем
(59)
Поэтому
(60)
Соотношение (60) выражает собой теорему Грина.
Получим далее другую форму теоремы. Для этой цели первоначально заменим в соотношении (60) “ 
” на “ 
”, а “ 
” на “ 
”. Получаем
(61)
Теперь вычтем из уравнения (60) уравнение (61). Окончательно находим
(62)
Соотношение (62) и выражает собой теорему Грина, представленную в более симметричной форме относительно “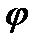 
” и “ 
”.
|
|
|
Уже отмечалось, что для применимости теоремы Гаусса-Остроградского достаточно потребовать непрерывность функцииа(r) и конечность ее первых частных производных в области V. Поэтому для применимости теоремы Грина достаточно потребовать, чтобы функция “ 
” и “ 
” были конечными, непрерывными и обладающими в области интегрирования конечными частными производными первого и второго порядков.
Дата добавления: 2018-06-27; просмотров: 943; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!