Задачи для самостоятельного решения

1. Доказать следующие соотношения для дивергенции сложной функции:

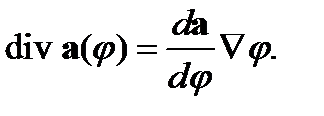(134)

2.Вычислить градиент функции 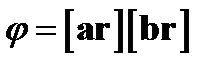.Здесьаи b– постоянные векторы.

3.Вычислить градиент функции 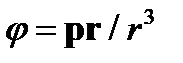,гдер –постоянный вектор.

4.Вычислить ротор вектора 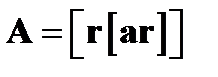,гдеа – постоянный вектор.

5.Преобразовать интеграл 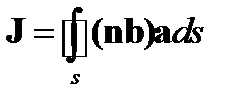 по замкнутой поверхности (b –постоянный вектор, n –орт нормали к поверхности) в интеграл по объему.

6.Вычислить интеграл по замкнутой поверхности 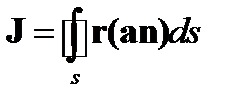, гдеа –постоянный вектор, n –орт нормали к поверхности.

7.Доказать, что интеграл 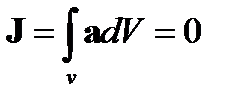 ,если внутри объема V вектора удовлетворяет условию diva= 0, а на границе объема – условию a_n=0.

8.Доказать следующую формулу векторного анализа: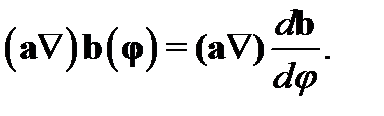

9.Доказать тождество .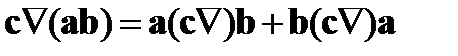

10. Преобразовать интеграл по объему 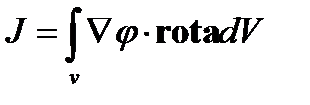 в интеграл по поверхности.

 

Криволинейные координаты.

Координатные поверхности и криволинейные координаты.

Когда поля обладают определенной симметрией, удобно использовать соответствующие криволинейные системы координат. Например, в случае сферической симметрии целесообразно использовать сферическую систему координат. Будем обозначать криволинейные координаты точки какq₁,q₂,q₃. Между этими координатами и декартовыми координатами x₁,x₂,x₃ предполагается взаимно однозначное соответствие, определяемое следующими формулами

x₁=x₁(q₁,q₂,q₃), x₂=x₂(q₁,q₂,q₃), x₃=x₃(q₁,q₂,q₃) (135)

Три поверхности

q_i=q_i(x_1,x₂,x₃)=C_i(136)

называется координатными поверхностями, а линии пересечения двух координатных поверхностей называются координатными линиями. В силу определения (136) вдоль координатной линии две координаты q_i сохраняют постоянные значения. Таким образом, вдоль координатной линии изменяется только одна координата. Орты криволинейной системы координат е₁, е₂,е₃ в каждой точке направляют вдоль касательных к соответствующим координатным линиям в сторону возрастания переменных. Мы будем здесь рассматривать только ортогональные системы координат, в которых орты е₁, е₂,е₃ являются взаимно перпендикулярными. Единичные векторы е₁, е₂,е₃ берутся в таком порядке, чтобы их совокупность образовывала правую тройку векторов. Коренное отличие криволинейны координат от декартовых заключается в том, что орты е₁, е₂,е₃, вообще говоря, изменяют свои направления при переходе от одной точки пространства к другой. Данные обстоятельство необходимо учитывать, в частности, при дифференцировании выражений , содержащих орты е₁, е₂,е₃.

    В цилиндрической системе координат

, ,

 

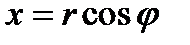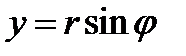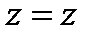
Координатными поверхностями являются следующие поверхности

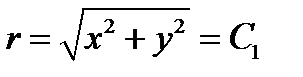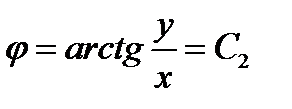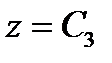,  ,     (137)

Координатными линиями являются окружности с центром на оси z, лучи, перпендикулярные к оси z и начинающиеся на этой оси, и прямые, параллельные оси z. Координатные линии и орты координатных осей изображены на рис. Видно, что векторы 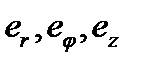 образуют правую тройку.

Коэффициенты Ламе

В декартовых координатах малое приращение радиус-вектора определяется формулой

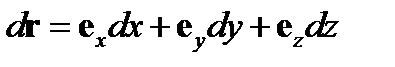(138)

В произвольных координатах

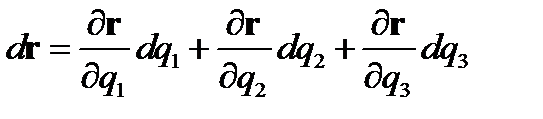(139)

Частная производная 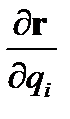 вычисляется как предел отношения  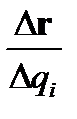при перемещении конца радиус-вектора rвдоль координатной линии q_i. . Из рисунка, на котором в указанном направлении вдоль кривой монотонно растет q_i ,видно, что при уменьшении ∆q_i и соответствующем уменьшении ∆rвектор ∆rприближается к касательной к координатной линии q_i и направлен в сторону увеличения q_i. Следовательно, вектор  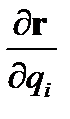будет направлен по касательной к координатной линии q_i , а его направление совпадает с направлением орта е_i. Поэтому можно записать 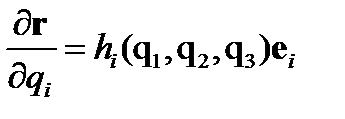.(140)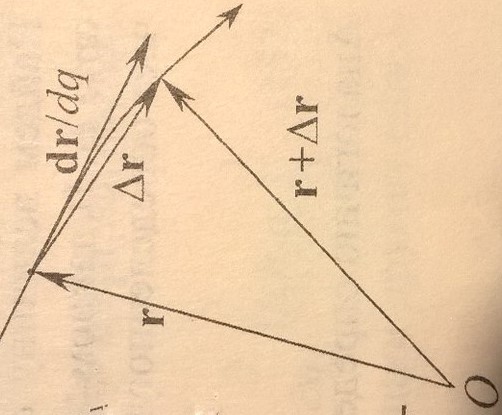

Три величины h₁,h₂,h₃ называются коэффициентами

Ламэ. Они представляют собой, очевидно,

 модули векторов                                                                                                               

 , , .

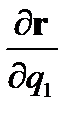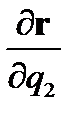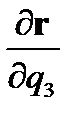Найдем соотношение, позволяющее вычислять коэффициенты Ламэ. Из формулы (140) находим

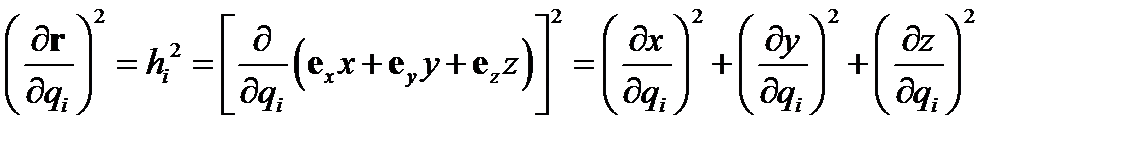
                                                                                                                                    (141)

Отсюда получим искомое выражение

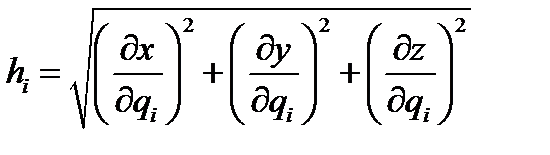(142)

    В цилиндрической системе координат ( 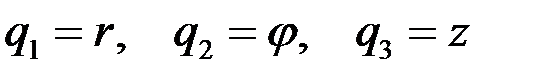) из формулы (142) находим

h₁=1, h₂=r, h₃=1 .(143)

В сферической системе координат (q₁=r, q₂=θ, q₃=φ)

x=rsinθcosφ, y=rsinθ sin φ, z=r cos φ.(144)

Поэтому для сферической системы координат

h₁=1, h₂=r, h₃=rsinθ.                           (145)      

Используя формулы (139),(140), имеем

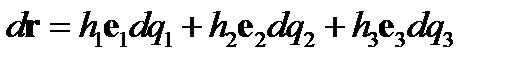.    (146) 

Отсюда находим квадрат элементарной длины

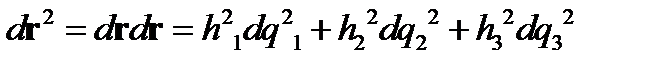   (147)  

Определим элементарный параллелепипед в данной области поля. Для этой цели из данной точки поля в направлении е₁ отложим вектор 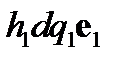в направлении е₂ –вектор 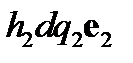, в направлении е₃–вектор 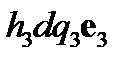,построим на этих векторах бесконечно малый параллелепипед. Площади граней этого параллелепипеда равны

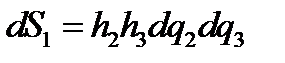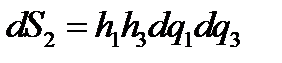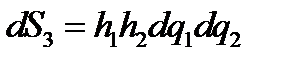 , , (148)

Здесь dS₁ –площадь грани, перпендикулярной к вектору е_{1, и} т .д. Объем параллелепипеда, очевидно, равен

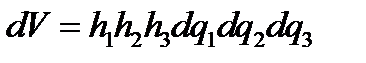(149)

---

Дата добавления: 2018-06-27; просмотров: 673; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!