Определение тензора в 3-мерном пространстве
Итак,тензором второго ранга в трехмерном пространстве называется девятикомпонентная величина 
, которая преобразуется при поворотах системы координат по следующему закону :
. (22)
Напомним, что здесь по повторяющимся индексам (немым индексам) производится суммированиеот 1 до 3. Так что в соотношении (22) стоит двойная сумма
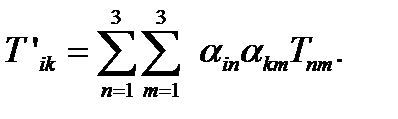(23)
Аналогично определяется тензор третьего ранга. Тензором третьего ранга называется двадцатисемикомпонентная величина 
, которая преобразуется при поворотах системы координат по следующему закону :
. (24)
В соотношении (24) фигурирует тройная сумма
Тензор r-го ранга в трехмерном пространстве определяется как 
- компонентная величина 
, которая преобразуется при поворотах системы координат по следующему закону :
. (25)
Величины 
наз.компонентами тензора. Компоненты 
наз. диагональными.
Еще раз отметим следующее.
По правилам индексных обозначений буквенный индекс может встречаться в каждом члене тензорного соотношения только один или два раза. Если индекс встречается один раз, то принимает значения 1,2,3 (в трехмерном пространстве). Неповторяющиеся индексы называются свободными. Повторяющиеся индексы называются немыми, и по ним производится суммирование. В правильно записанном тензорном соотношении ни один индекс не должен встречаться более двух раз.
|
|
|
Тензор r-го ранга называется истинным тензором или просто тензором, если при инверсии системы координат он преобразуется как произведение r координат, то есть если компоненты тензора при инверсии умножаются на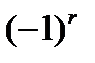 
:
. (26)
Тензор r-го ранга называется псевдотензором, если при инверсии системы координат его компоненты преобразуются по следующему закону:
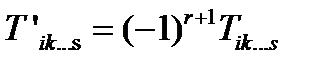. (27)
Тензор r-го ранга называется симметричным относительно двух своих индексов(например, индексов i и k), если его компоненты при перестановки этих индексов не изменяются. Тензор r-го ранга называется антисимметричным относительно двух своих индексов, если его компоненты при перестановке этих индексов изменяют знак. Тензор r-го ранга называется абсолютно симметричным, если его компоненты не изменяются при перестановке любой пары индексов. Тензор r-го ранга называется абсолютно антисимметричным, если его компоненты изменяют знак при перестановке любой пары индексов.
Операции сложения и умножения тензоров
Операции сложения тензоров и умножения их на скаляры определяются очевидным образом . Ясно, что складывать можно только тензоры одного ранга.Имеем по определению
|
|
|
.
Произведением тензоров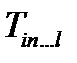 
(ранга r) и 
(ранга s ) называется тензор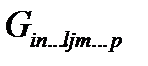 
, 
которого определяются по формуле
(28)
Ранг произведения тензоров равен сумме рангов тензоров-сомножителей.
Свертка тензора и скалярное произведение тензоров
Свертыванием тензора по паре индексов называется следующая операция: два индекса в компонентах тензора полагаются одинаковыми, и по ним осуществляется суммирование. Величина, которая получается при этом, называется сверткой тензора. Свертка тензора второго ранга является, очевидно, скаляром. Этот скаляр называется следом тензора или шпуром тензора.
Умножение тензоров с последующим свертыванием называется скалярным произведением тензоров.
Абсолютно антисимметричный единичный псевдотензор третьего ранга
Символ Кронекера 
, заданный одинаково во всех системах координат, является симметричным тензором второго ранга. Рассмотрим двадцатисемикомпонентную величину 
, определенную во всех декартовых системах координат следующим образом: 
, а при перестановке любых двух индексов величина 
изменяет знак. Отсюда вытекает, что 
равны нулю, если равны любые два индекса. Величины 
равны 1, если все индексы различны и образуют циклическую перестановку последовательности 1,2,3. Величины 
равны -1, если все индексы различны и образуют циклическую перестановку последовательности 3,2,1. Из 27величин 
21 величина равна нулю, три величины равны 1 и три величины равны -1. Можно доказать , что совокупность величин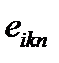 
образует абсолютно антисимметричный единичный псевдотензор третьего ранга. Этот тензор называется еще тензором Леви-Чивиты.
|
|
|
С помощью тензора 
можно записать связь между ортами декартовой системы координат в виде
(29)
Выполняются следующие полезные равенства:
(30)
(31)
Компоненты векторного произведения
Компоненты векторного произведения можно записать с помощью рассмотренного псевдотензора в следующем виде:
. (32)
Формулы (32) можно проверить, например, непосредственно.
|
|
|
Отметим, что определитель
можно представить в виде
(33)
Формулу (33) можно также проверить, например, непосредственно.
Главная ось тензора
Рассмотрим произвольный симметричный тензор второго ранга 
и произвольное направление 
Определим вектор 
Если направление 
таково, что вектор 
параллелен вектору , то выполняется соотношение
(34)
В этом случае направление называют главной осью тензора 
Соотношению (34) можно, очевидно, придать форму
(35)
Выражение (35) представляет собой однородную систему относительно трех неизвестных 
Длятого чтобы однородная система (35) имела нетривиальное решение, должно выполняться следующее соотношение (характеристическое уравнение):
. (36)
Кубическое уравнение (36) имеет три решения 
которые называются главными значениями тензора 
. Симметричный тензор с действительными компонентами имеет действительные главные значения. Если все корни уравнения (36) различны, то три главные оси тензора 
взаимно ортогональны. В главных осях тензор сводится к диагональной форме
(37)
Дата добавления: 2018-06-27; просмотров: 927; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!