Скалярное произведение векторов

По определению

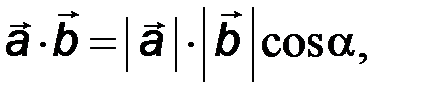
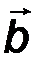
ab

a

Рис. 1. К определению скалярного произведения

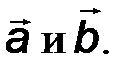где a–угол между векторами  Но 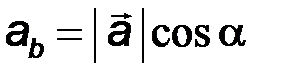 есть проекция вектора  на направление вектора 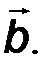 На рис. 1 ей отвечает расстояние, измеряемое в направлении вектора  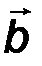от общей точки начала этих двух векторов до основания перпендикуляра, опущенного из конца вектора  на прямую, проходящую вдоль вектора 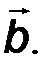 Проекция положительна, если cosa>0, и отрицательна, когда векторы  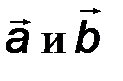составляют тупой угол. Иногда под проекцией понимают не число со знаком (имеющее размерность соответствующей физической величины), а рассматривают векторную проекцию–вектор величиной |a_b|, имеющий направление вектора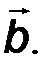

Скалярное произведение можно представить в следующих равноценных формах

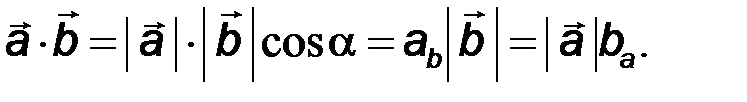          (2)

Очевидно, 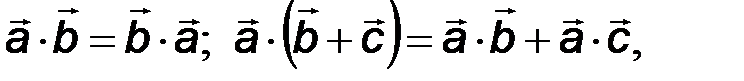 то есть скалярное произведение коммутативно и дистрибутивно, 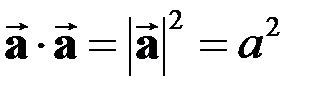, , 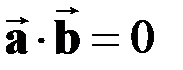если сомножители взаимно перпендикулярны или если один из сомножителей является нулевым вектором, , .

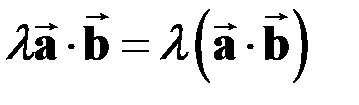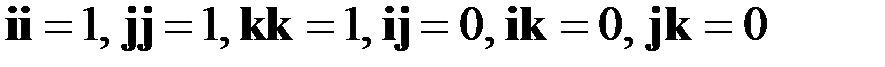Пусть даны два вектора

 

, .

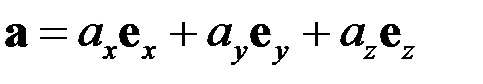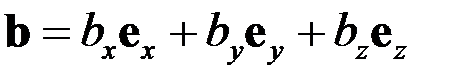Найдем скалярное произведение этих векторов, перемножая их как многочлены (что законно в силу указанных выше свойств). Отсюда имеем

 

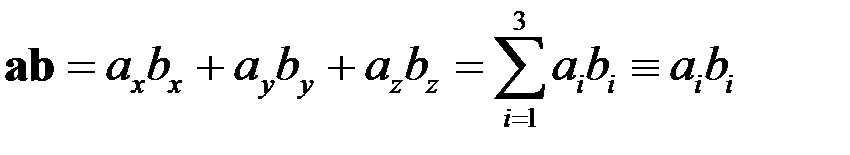
 В этой записи использовано правило суммирования Эйнштейна по повторяющимся индексам. Выше была доказана теорема:

 

Скалярное произведение векторов равно сумме произведений их одноименных компонент.

 

 

Векторное произведение                                                                                                               

Векторным произведением вектороваи b называется вектор

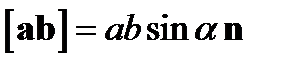,(3)

где 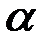 – угол между векторами аи b(наименьший угол), а n– единичный вектор нормали к плоскости, в которой лежат векторы аи b, причем последовательность векторов a,b,nобразует правовинтовую систему. Векторное произведение еще часто обозначают так

.

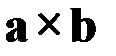Направление n может быть определено и по правилу правого буравчика. Правый винт необходимо поворачивать от вектора aк вектору bв направлении наименьшего угла, тогда направление перемещения винта будет совпадать с направлением векторного произведения.

Укажем еще одно правило определения направления векторного произведения. Если смотреть с конца вектора n,то поворот от вектораа к вектору b в направлении наименьшего угла должен быть виден совершающимся против часовой стрелки. Поэтому для определения направления векторного произведения можно первоначально указать произвольное направление. Если это направление выбрано правильно, то с конца вектора nповорот от вектораа к вектору bв направлении наименьшего угла будет виден совершающимся против часовой стрелки. Если это направление выбрано неправильно, то оно должно быть заменено на противоположное.

Модуль векторного произведения 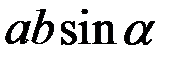равен площади параллелограмма, построенного на данных векторах.

   Свойства

1)

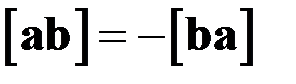
2)

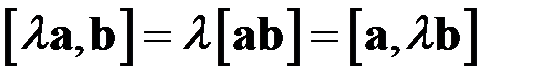
3)

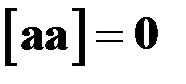
4)

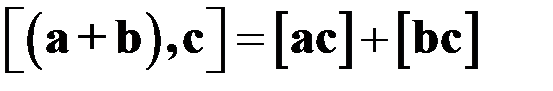
5) .

 

 

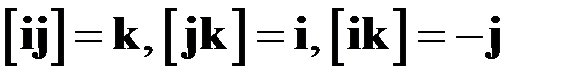Выразим векторное произведение через компоненты векторов.

 

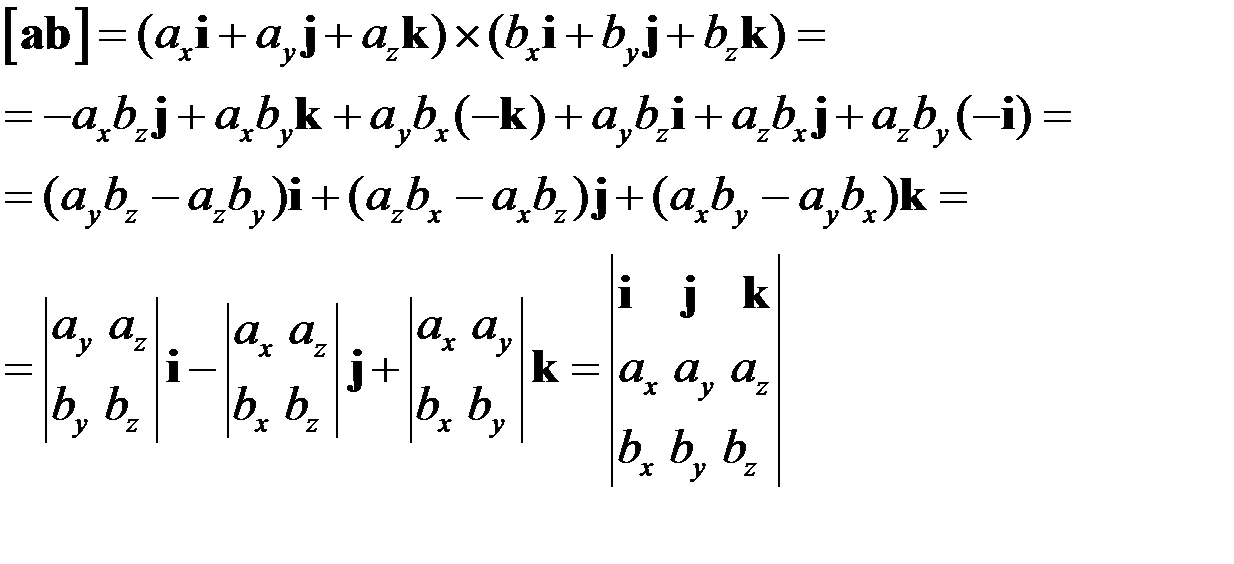
Итак, в декартовой системе координат векторное произведение может быть записано в виде определителя

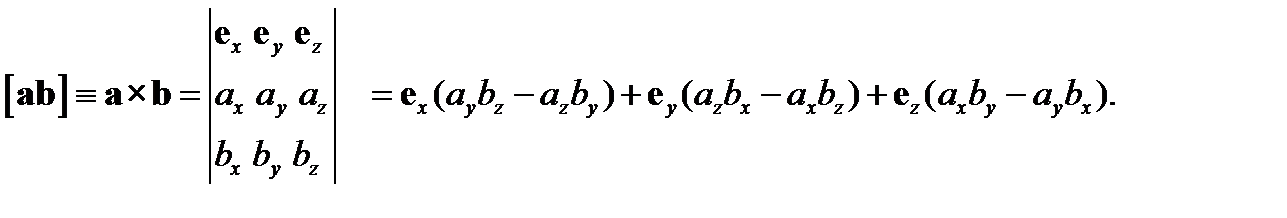(4)           

Здесь 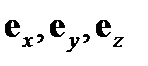- орты координатных осей. Отметим, что формула(4) сохраняется и в любой другой оргональной системе координат, если в данном выражении орты  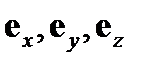заменить на тройку базисных  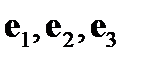другой оргональной системе координат.

В физике довольно часто используется так называемое правило <<бац минус цаб>> для двойного векторного произведения

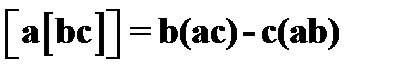.                                              (5)

---

Дата добавления: 2018-06-27; просмотров: 639; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!