Дифференциальные соотношения векторного анализа
Ряд дифференциальных соотношений векторного анализа был приведен выше. Выведем некоторые другие формулы, которые часто применяются в физике. Прежде всего, отметим, что
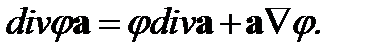 (63)
(63)
Соотношение (63) непосредственно получается в декартовой системе координат.. Далее, имеем
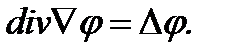 (64)
(64)
Простое и важное соотношение (64) непосредственно вытекает из формулы (58) предыдущего раздела, в которой следует положить 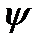 =1.
=1.
Докажем, что
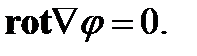 (65)
(65)
Используя представление ротора в виде (36), находим
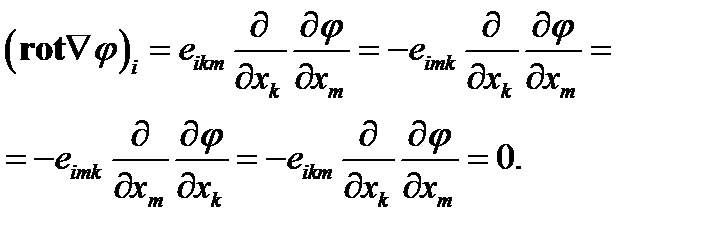 (66)
(66)
В соотношении (66) мы, первоначально воспользовавшись свойством антисимметричности тензора “ 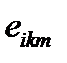 ” ,затем изменили порядок дифференцирования и, наконец, произвели замену обозначений немых индексов (индекс m был заменен индексом k и одновременно индекс k был m). После этих преобразований мы получили выражение, которое отличается от первоначального знаком. Поскольку эти выражения равны, то в этом случае преобразуемая величина, очевидно, должна быть равна нулю.
” ,затем изменили порядок дифференцирования и, наконец, произвели замену обозначений немых индексов (индекс m был заменен индексом k и одновременно индекс k был m). После этих преобразований мы получили выражение, которое отличается от первоначального знаком. Поскольку эти выражения равны, то в этом случае преобразуемая величина, очевидно, должна быть равна нулю.
Отметим, что соотношение (65) также непосредственно вытекает из формулы Стокса (41), в которой следует положить 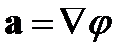 и воспользоваться достаточно очевидным соотношением
и воспользоваться достаточно очевидным соотношением
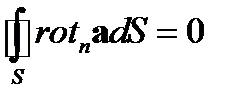 . (67)
. (67)
|
|
|
Соотношение (67) означает, что поток ротора произвольного вектора через произвольную замкнутую поверхность равен нулю. Разумеется, в данном выводе существенно используется фактор произвольности контура L и области интегрирования S, который позволяет из равенства нулю интеграла делать вывод о равенстве нулю подынтегрального выражения.
Докажем, что дивергенция произвольного ротора равна нулю. При этом будем использовать те же приемы доказательства, что и в предыдущем примере. Имеем
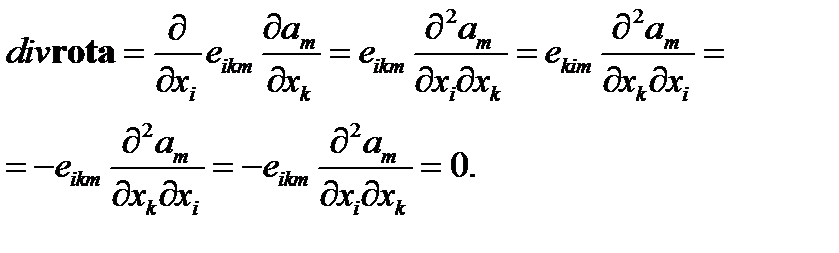 (68)
(68)
В соотношении (68) мы первоначально изменили обозначения немых индексов (индекс i заменили индексом k и одновременно заменили индекс k индексом i), затем воспользовались свойством антисимметричности тензора 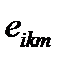 и, наконец, изменили порядок дифференцирования.
и, наконец, изменили порядок дифференцирования.
Отметим, что данный результат может быть также получен из формулы Гаусса-Остроградского, в которой следует положить 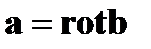 . Используя соотношение (67), находим
. Используя соотношение (67), находим
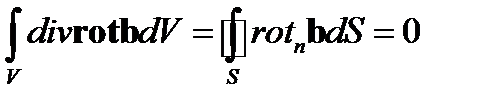 . (69)
. (69)
В силу произвольности объема V из формулы (69) вытекает искомое равенство
 (70)
(70)
Соотношения (65), (70) мы получили и прямым вычислением в декартовой системе координат.
|
|
|
Важно отметить, что основные формулы векторного анализа, в которые входят инвариантные выражения 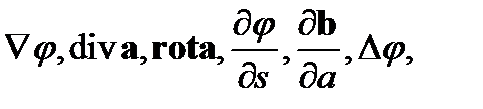 тоже носят инвариантный характер (то есть не зависят от выбора той или иной системы координат), хотя при доказательстве их могла использоваться конкретная декартовая система координат.
тоже носят инвариантный характер (то есть не зависят от выбора той или иной системы координат), хотя при доказательстве их могла использоваться конкретная декартовая система координат.
Докажем, что
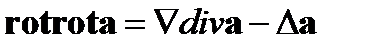 (71)
(71)
Используя рассмотренное ранее представление компонент ротора, имеем
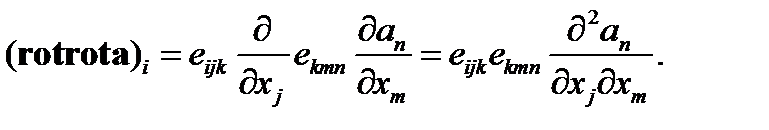 (72)
(72)
Согласно соотношению (I.20),
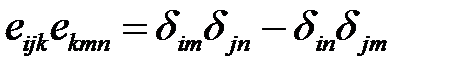 . (73)
. (73)
Подставив (73) в (72), находим
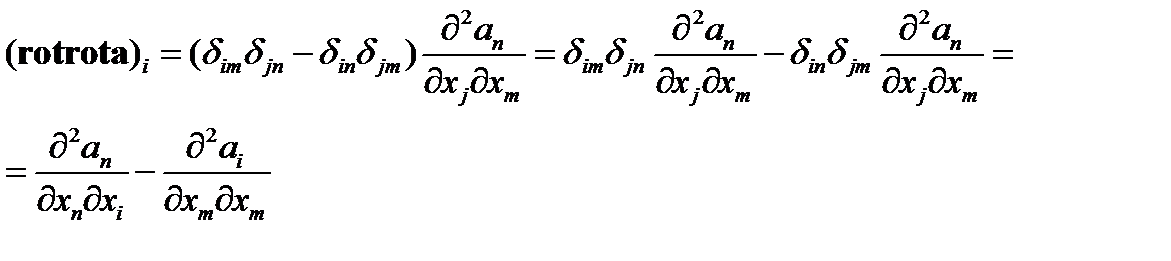 (74)
(74)
Далее имеем
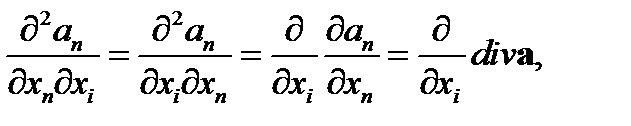
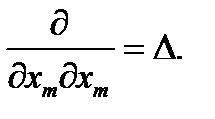 (75)
(75)
Теперь, используя (75), записываем соотношение(74) в виде
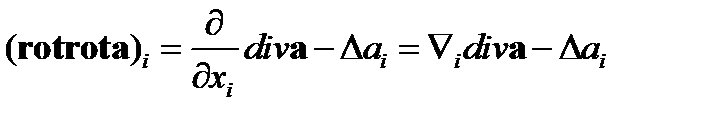 . (76)
. (76)
Три скалярных соотношения (76) и эквивалентны векторному соотношению (71).
Установим следующую важную формулу векторного анализа:
 (77)
(77)
Имеем
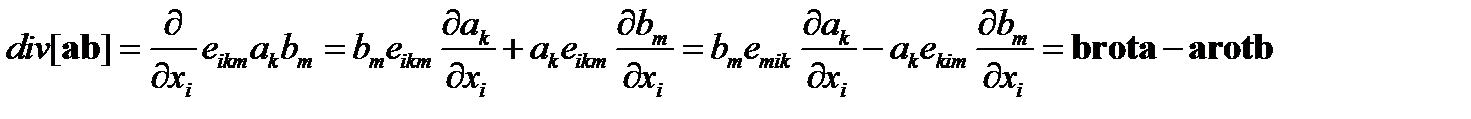 (78)
(78)
В преобразованиях (78) были использованы свойство антисимметричности тензора 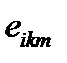 , представление ротора вектора в виде (38). Докажем, что
, представление ротора вектора в виде (38). Докажем, что
|
|
|
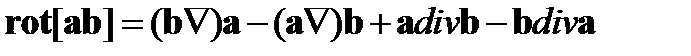 (79)
(79)
Имеем
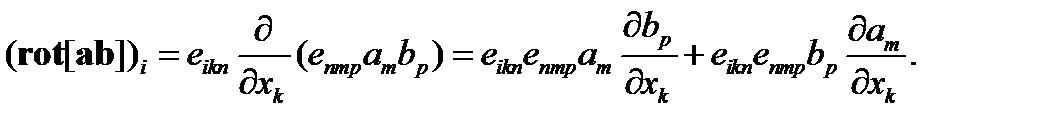 . (80)
. (80)
Преобразуем первое слагаемое в правой части (80). Используя формулу (I.30) и свойства символов Кронекера, находим
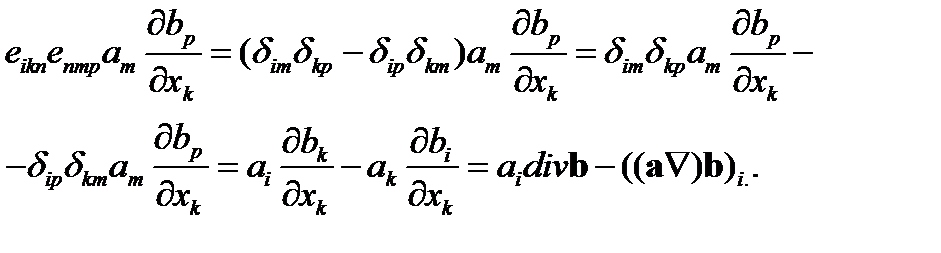 (81)
(81)
Второе слагаемое в правой части (80) можно представить в виде
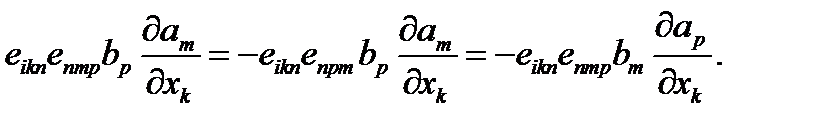 (82)
(82)
В преобразованиях (82) использовано свойство антисимметричности тензора 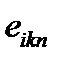 и далее произведено переобозначение немых индексов(индекс m заменен индексом p, а индекс p заменен индексом m). Теперь второе слагаемое в правой части (80) отличается от первого слагаемого только знаком и заменой
и далее произведено переобозначение немых индексов(индекс m заменен индексом p, а индекс p заменен индексом m). Теперь второе слагаемое в правой части (80) отличается от первого слагаемого только знаком и заменой 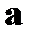 на
на 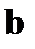 и
и 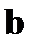 на
на 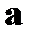 . Поэтому
. Поэтому
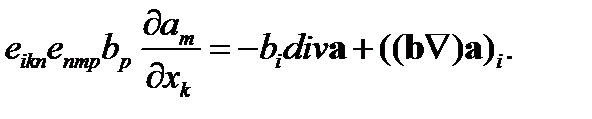 (83)
(83)
Теперь находим
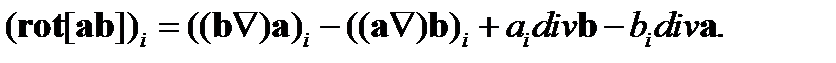 (84)
(84)
Три скалярных соотношения (84) эквивалентны векторному тождеству (79).
Докажем, что
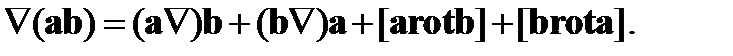 (85)
(85)
Для доказательства векторного соотношения (85) рассмотрим компоненту i суммы двух последних слагаемых в формуле (85). Имеем
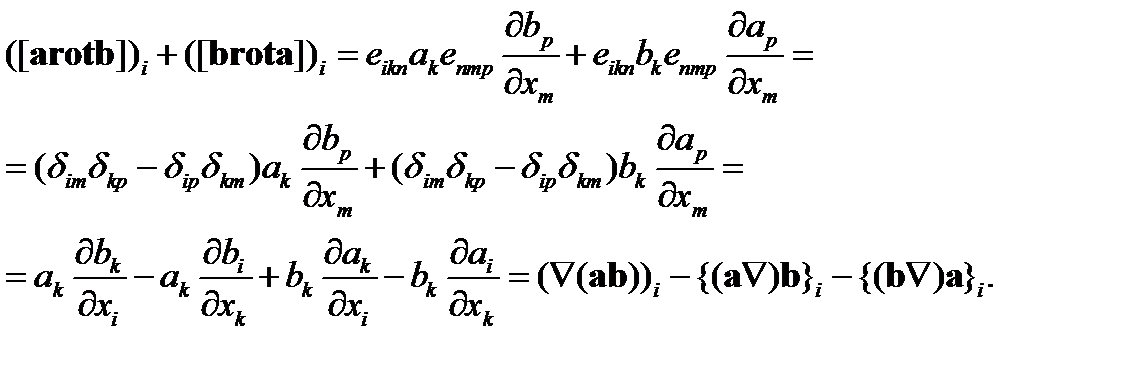
Соотношение (85) доказано.
Примеры решения задач
11. Доказать формулу векторного анализа
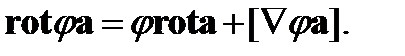 (86)
(86)
|
|
|
Решение.
Для решения используем представление ротора и векторного произведения с помощью тензора 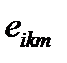 . Имеем
. Имеем
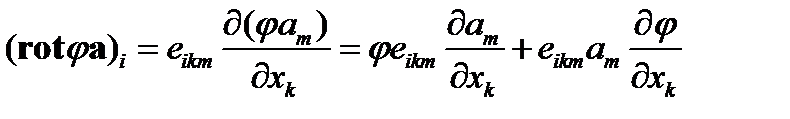 (87)
(87)
В первое слагаемое в правой части (87) входит, очевидно, компонента i ротора вектора 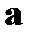 , а второе же слагаемое представляет собой компоненту i векторного произведения вектора с компонентами
, а второе же слагаемое представляет собой компоненту i векторного произведения вектора с компонентами 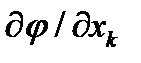 на вектор
на вектор 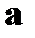 . Но вектор с компонентами
. Но вектор с компонентами 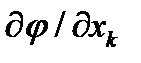 есть
есть 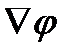 . Итак, получаем
. Итак, получаем
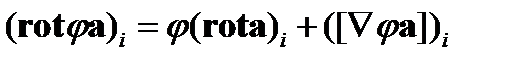 (88)
(88)
Из соотношения (88) и вытекает искомая формула (86).
12. Найти дивергенцию и ротор вектора 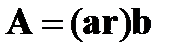 , где
, где 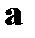 и
и 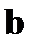 - постоянные векторы.
- постоянные векторы.
Решение.
Используя формулу (63), находим
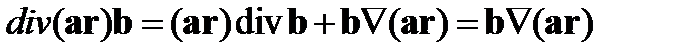 (89)
(89)
Далее получаем
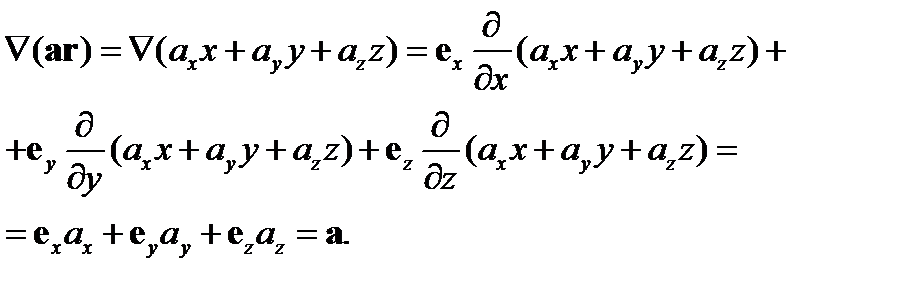 (90)
(90)
Поэтому, согласно (89), (90), определяем
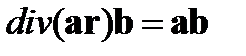 . (91)
. (91)
Найдем теперь 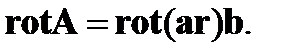 Используя формулу (86) из первой задачи, получаем
Используя формулу (86) из первой задачи, получаем
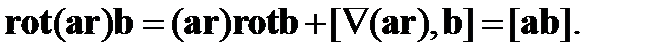 (92)
(92)
Соотношение (92) и представляет собой решение второй задачи.
13. Определить ротор вектора 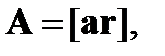 где
где 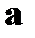 - постоянный вектор.
- постоянный вектор.
Решение.
Используя представление ротора и векторного произведения с помощью тензора 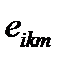 , находим
, находим
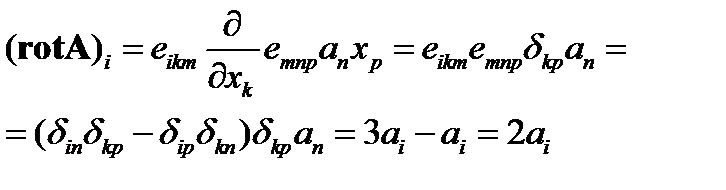 (93)
(93)
Из соотношения (93) вытекает, что
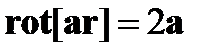 . (94)
. (94)
Отметим, что в (93) использовались свойства символа Кронекера (единичного тензора). Очевидно, что
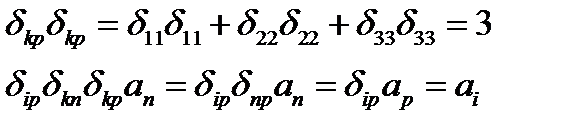 (95)
(95)
Решение (94) может быть получено и другими способами. Можно, например, воспользоваться полученной выше формулой (79). Находим
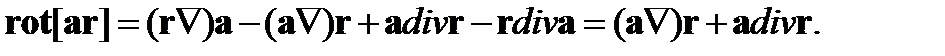 (96)
(96)
Теперь из соотношения (98) имеем
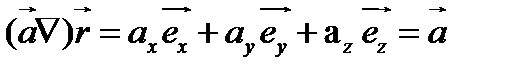 (97)
(97)
Подставляя (97), (99), в (96) , получаем формулу (94).
14. Найти градиент 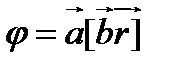 , где
, где 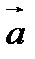 и
и 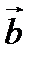 - постоянные векторы.
- постоянные векторы.
Решение
Первоначально изменим порядок сомножителей в смешенном произведении
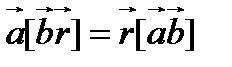 (98)
(98)
Далее введем обозначение
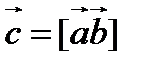 (99)
(99)
Вектор 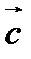 , очевидно, является постоянным. Используя (98), находим
, очевидно, является постоянным. Используя (98), находим
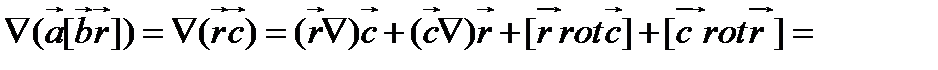
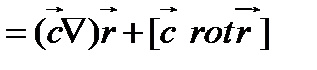 (100)
(100)
Выражение (100) еще упрощается, так как
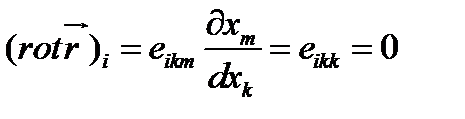 (101)
(101)
Из соотношения (101), очевидно, вытекает
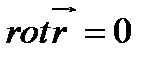 (102)
(102)
Поэтому находим
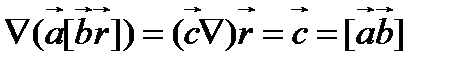 (103)
(103)
Укажем другой способ решения. Для этого представим смешанное произведение с помощью тензора 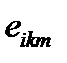 в виде
в виде
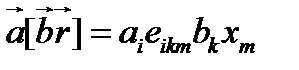 (104)
(104)
Далее последовательно получаем
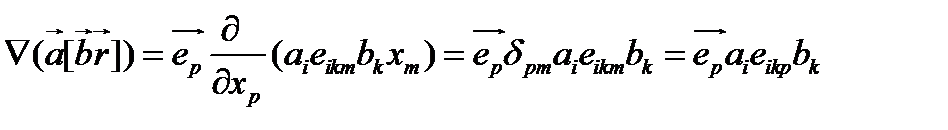 (105)
(105)
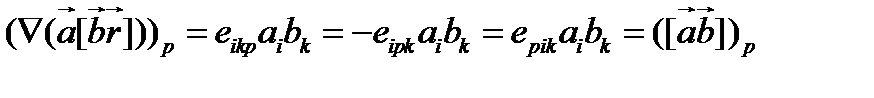 (106)
(106)
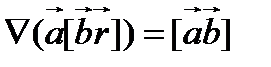 . (107)
. (107)
Отметим, что соотношение (105) может быть, конечно, получено путем прямого вычисления с использованием явного вида смешанного произведения.
15. Вычислить интеграл 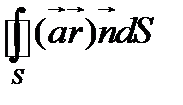 , где
, где 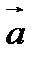 -постоянный вектор,
-постоянный вектор, 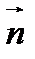 орт нормали к поверхности
орт нормали к поверхности
Решение
Для решения задачи умножим интеграл на произвольный постоянный вектор 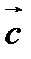 и преобразуем полученное выражение. Используя теорему Гаусса-Остроградского, имеем
и преобразуем полученное выражение. Используя теорему Гаусса-Остроградского, имеем
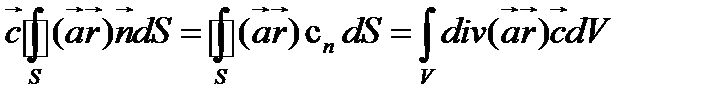 (108)
(108)
Упростим подынтегральное выражение в формуле (108). Используя соотношение (63), находим
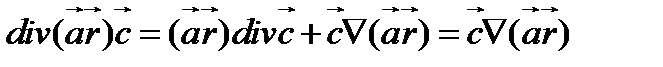 (109)
(109)
Градиент скалярного произведения векторов 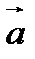 и
и 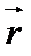 в (109) был вычислен во втором примере и оказался равным
в (109) был вычислен во втором примере и оказался равным 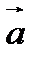 . Поэтому
. Поэтому
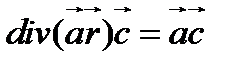 (110)
(110)
Используя (110) , получаем
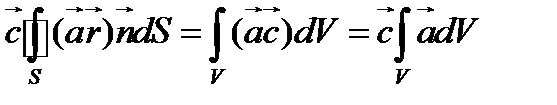 (111)
(111)
Так как постоянный вектор 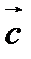 является произвольным, из выражения (111) вытекает
является произвольным, из выражения (111) вытекает
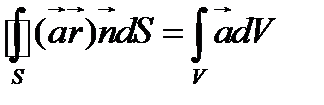 (112)
(112)
Наконец, поскольку вектор 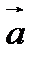 является постоянным, окончательно находим
является постоянным, окончательно находим
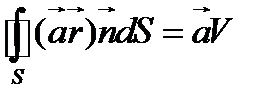 (113)
(113)
16. Преобразовать интеграл по замкнутой поверхности 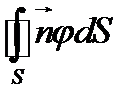 (
( 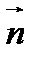 -орт нормали к поверхности) в интеграл по объему, заключенному внутри поверхности. На основании решения данной задачи дать инвариантное интегральное определение градиента функции.
-орт нормали к поверхности) в интеграл по объему, заключенному внутри поверхности. На основании решения данной задачи дать инвариантное интегральное определение градиента функции.
Решение.
Как и в предыдущей задаче, для проведения необходимых преобразований интеграл на произвольный постоянный вектор 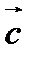 . Такой прием позволяет воспользоваться теоремой Гаусса-Остроградского. Имеем
. Такой прием позволяет воспользоваться теоремой Гаусса-Остроградского. Имеем
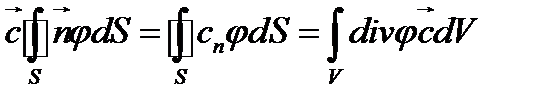 (114)
(114)
Далее, используя формулу (63), находим
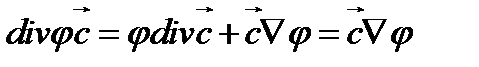 (115)
(115)
Подставляя (115) в (114), получаем
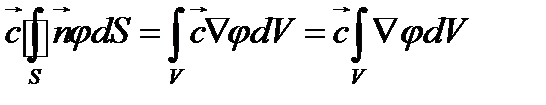 (116)
(116)
Так как постоянный вектор 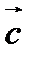 является произвольным, из выражения (116) вытекает
является произвольным, из выражения (116) вытекает
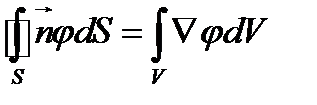 (117)
(117)
Выражение (117) и представляет собой окончательный результат преобразования.
Рассмотрим теперь произвольную точку поля Р. Пусть 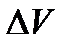 -некоторый малый объем, ограниченный поверхностью
-некоторый малый объем, ограниченный поверхностью 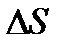 , причем точка Р содержится внутри данного объема. Для данного случая соотношение (117) принимает вид
, причем точка Р содержится внутри данного объема. Для данного случая соотношение (117) принимает вид
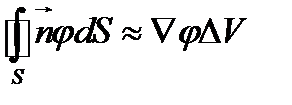 . (118)
. (118)
В приближенном равенстве (118) значение 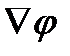 взято в точке Р. Из формулы (118) вытекает следующее выражение для градиента
взято в точке Р. Из формулы (118) вытекает следующее выражение для градиента 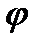 в точке Р
в точке Р
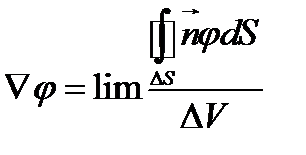 при
при 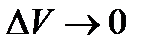 (119)
(119)
В соотношении (119) предполагается, что предельный переход осуществляется стягиванием объема 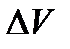 к точке Р.
к точке Р.
17. Доказать тождество
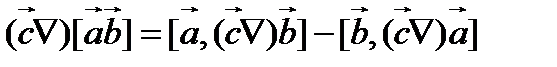 (120)
(120)
Решение
Будем использовать представление векторного произведения с помощью тензора 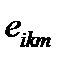 . Для левой части тождества (120), очевидно, имеем
. Для левой части тождества (120), очевидно, имеем
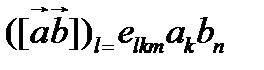 (121)
(121)
(122)
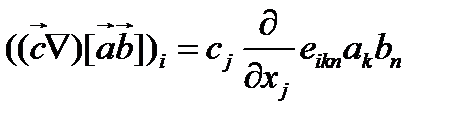
Производя дифференцирование в соотношении (122), находим
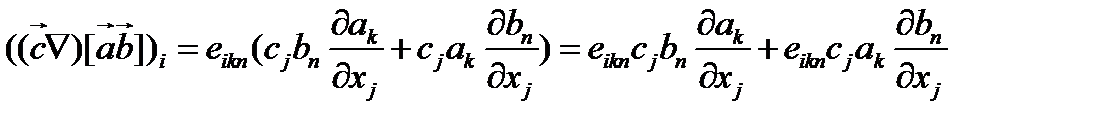 (123)
(123)
Далее имеем
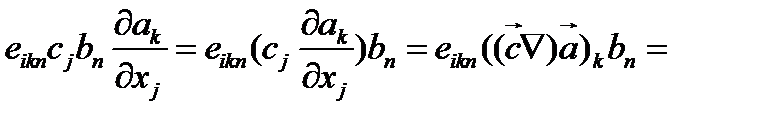 (124)
(124)
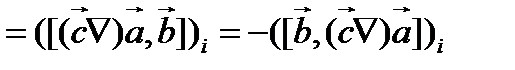
Левую часть соотношения (124) мы просто представили как компоненту iвекторного произведения. Для этой цели был выделен комплекс 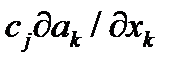 , который представляет собой компоненту kвектора
, который представляет собой компоненту kвектора 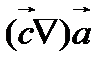 .
.
Аналогично преобразуется второе слагаемое в правой части (123).
Находим
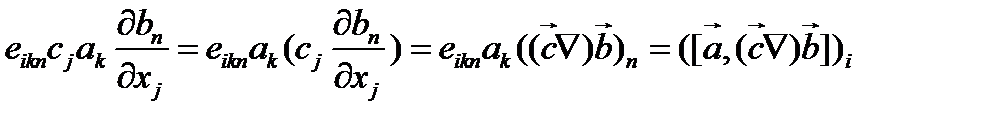 (125)
(125)
Теперь, используя соотношение (123)-(125), получаем
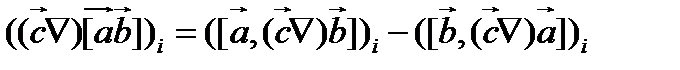 (126)
(126)
Три скалярных выражения (126), очевидно, эквивалентны искомому векторному тождеству (121)
18. Доказать теорему Гаусса-Остроградского для трехмерного тензора второго ранга:
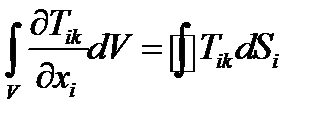 (127)
(127)
Решение
Для доказательства применим теорему Гаусса-Остроградского к вектору 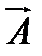 :
: 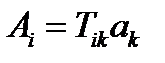 , где
, где 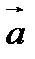 -произвольный постоянный вектор. Имеем
-произвольный постоянный вектор. Имеем
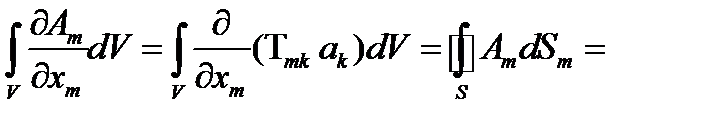 (128)
(128)
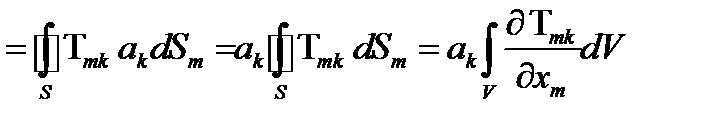
Из последнего равенства в (128),в силу произвольности вектора 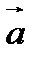 , и вытекает теорема Гаусса-Остроградского (127) для тензора второго ранга (использование в (128) немого индекса m вместо немого индекса i в (127), конечно, не является принципиальным в соответствии с правилами обозначения немых индексов).
, и вытекает теорема Гаусса-Остроградского (127) для тензора второго ранга (использование в (128) немого индекса m вместо немого индекса i в (127), конечно, не является принципиальным в соответствии с правилами обозначения немых индексов).
19. Вычислить 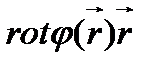
Решение
Используя формулу векторного анализа (86) и соотношение (104), находим
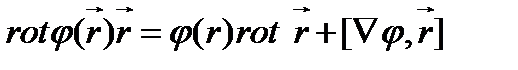 (129)
(129)
Так как 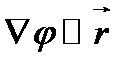 , то
, то 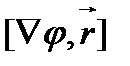 =0. Поэтому окончательно получаем
=0. Поэтому окончательно получаем
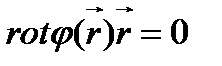 (130)
(130)
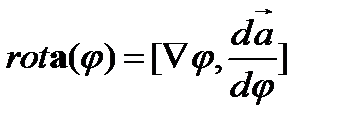 20.Доказать следующее соотношение для ротора сложной функции:
20.Доказать следующее соотношение для ротора сложной функции:
(131)
Решение.
Используя представление ротора с помощью тензора еikmи правило дифференцирования сложной функции, находим
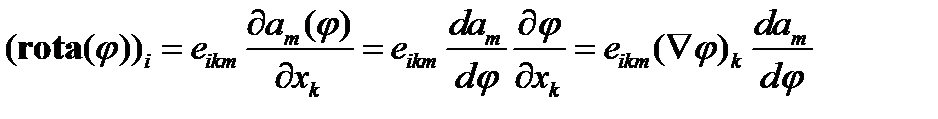 .
.
(132)
Из соотношения (132) непосредственно вытекает
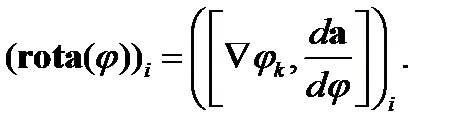 (133)
(133)
Действительно, 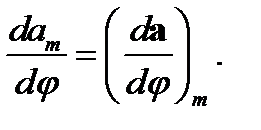 Формула (133) эквивалентна векторному равенству (131).
Формула (133) эквивалентна векторному равенству (131).
Дата добавления: 2018-06-27; просмотров: 634; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
