Формула прямого преобразования Лапласа
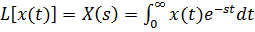 , (5)
, (5)
Формула обратного преобразования Лапласа
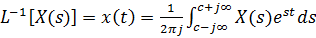 . (6)
. (6)
В результате прямого преобразования Лапласа некоторой функции времени x(t) получается функция X(s) комплексной переменной s=c+j 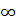 .
.
Эта функция называется изображением Лапласа функции x(t). В свою очередь x(t) называется оригиналом изображения X(s).
В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях и обозначается:
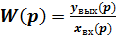 (7)
(7)
Передаточная функция представляет собой дробно-рациональную функцию W(p)комплексного переменного. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.
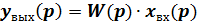 (8)
(8)
Передаточная функция разомкнутой системы имеет весьма большое значение в теории автоматического управления, так как многие методы анализа и синтеза основаны на использовании именно этой функции.
Передаточная функция замкнутой системы устанавливает связь между управляемой величиной и задающим воздействием при равенстве нулю возмущающих воздействий.
Передаточная функция замкнутой системы по ошибке определяет связь
между ошибкой и задающим воздействием в замкнутой системе при равенстве нулю возмущающих воздействий.
Знание передаточной функции разомкнутой системы позволяет найти выражение для ошибки и управляемой величины в функции задающего и возмущающих воздействий, а также характеристическое уравнение системы.
Передаточная функция разомкнутой системы может находиться непосредственно по структурной схеме и передаточным функциям входящих в нее звеньев
Если имеются уравнения всех звеньев системы управления, то описанием последней является система этих уравнений. Исключив из нее промежуточные переменные, можно получить одно дифференциальное уравнение высокого порядка (уравнение динамики САУ), связывающее интересующую нас выходную величину системы с входными величинами – каким либо возмущающим или задающим воздействиями. Наиболее просто это можно сделать, используя передаточные функции (рисунок 23).

Рисунок 23
Передаточная функция цепочки последовательно соединенных звеньев направленного действия: 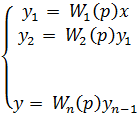 (9)
(9)
При последовательном соединении выходная величина каждого предшествующего звена является входным воздействием для последующего звена.
Исключив промежуточные переменные, получим:
y= 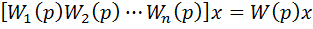 ,
,
где W(p)= 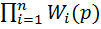 ,(10)
,(10)
то есть передаточная функция цепочки последовательно соединенных звеньев равна произведению передаточных функций звеньев.
Это значит, что такую цепочку можно заменить в структурной схеме одним эквивалентным звеном с передаточной функцией W(p) (рисунок 24).

Рисунок 24
При параллельном соединении на вход всех звеньев подается один и тот же сигнал, а выходные величины складываются.
Параллельное соединение звеньев направленного действия
Y= 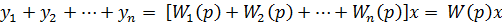 ,
,
Где W(p) = 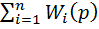 .(11)
.(11)
Таким образом, передаточная функция группы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев. В структурной схеме такую группу звеньев можно заменить одним эквивалентным звеном с передаточной функцией W(p)
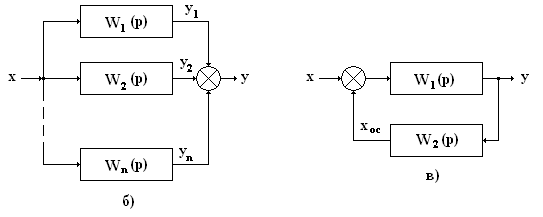
Рисунок 25
Для звена, охваченного обратной связью (рисунок 25), важно знать, является ли обратная связь положительной или отрицательной. Если обратная связь положительная, то сигнал обратной связи 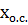 складывается с входным сигналом х. На схеме должен стоять «плюс» у суммирующего элемента. Если обратная связь отрицательная («минус» у суммирующего элемента), то сигнал обратной связи вычитается из входного сигнала. Схема описывается следующими уравнениями:
складывается с входным сигналом х. На схеме должен стоять «плюс» у суммирующего элемента. Если обратная связь отрицательная («минус» у суммирующего элемента), то сигнал обратной связи вычитается из входного сигнала. Схема описывается следующими уравнениями:
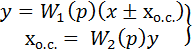 (12)
(12)
Исключив 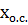 , получим
, получим
y= 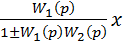 или y=
или y= 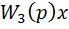 , где
, где
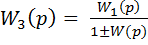 , а W(p) =
, а W(p) = 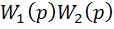 .(13)
.(13)
Здесь положительной обратной связи соответствует минус, а отрицательной – плюс.
Основные правила преобразования представлены в таблице (рисунок 26)
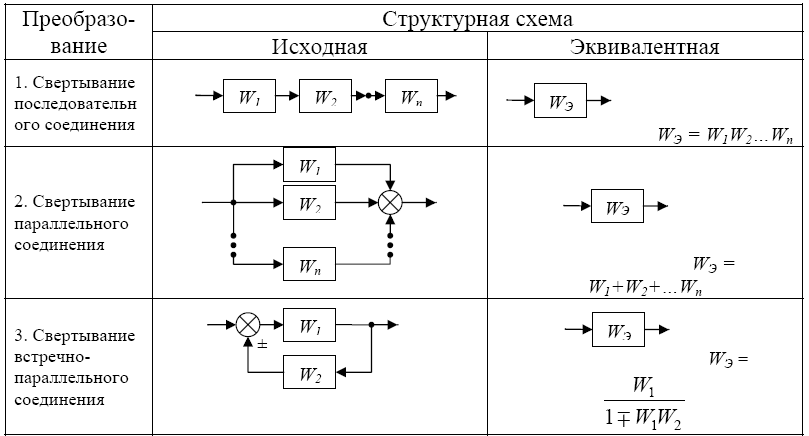
Рисунок 26

Мы поможем в написании ваших работ!
