Пропорциональное звено (усилительное)
Выходная величина этого звена прямо пропорциональна входной величине. Уравнение, связывающее выходную величину Y с входной X для безынерционного звена: y=kx, где k – коэффициент передачи (усиления).
После применения преобразования Лапласа, получим :
W(p) =  (14)
(14)
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется так:
H(p) = X(p)*W(p) = k  (15)
(15)
Выполняя обратное преобразование изображения переходной характеристики, получим:
h(t)= k*1(16)
Пропорциональное звено мгновенно (без инерции) реагирует на входное воздействие (рисунок 27). Выходная величина без запаздывания повторяет изменение входной величины, но только в другом масштабе. Звено равномерно пропускает сигналы всех частот.
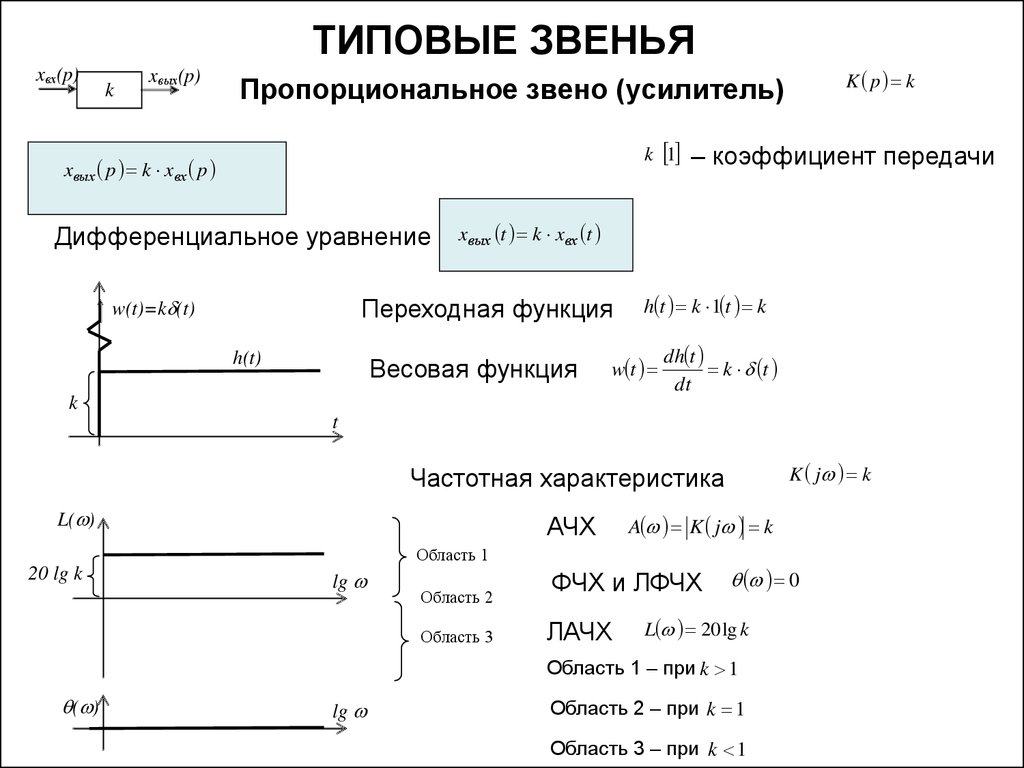
Рисунок 27
Инерционное звено 1-ого порядка (апериодическое)
В статике, т. е. когда входная и выходная величины не изменяются, они связаны линейной зависимостью Y=kX
Если в инерционном звене 1-ого порядка входная xвеличина изменится во времени, то выходная yбудет так же изменяться во времени, но повторяя изменение с некоторым запаздыванием – инерцией. В инерционном звене 1-ого порядка скорость изменения выходной величины yзависит от входной x, ипропорциональна разности между заданным и фактическим значениями выходной величины.
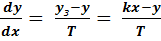 (17)
(17)
где:
y и x –значения соответственно выходного и входного сигналов, t – текущее значение времени, T – постоянная времени, которая определяет скорость протекания процесса или скорость реагирования, k – коэффициент передачи.
Умножив обе части уравнения (17) на Т, получим дифференциальное уравнение инерционного звена в канонической форме:
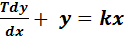 (18)
(18)
Всякое звено, независимо от физической природы и конструкции, описываемое уравнение (18) называется инерционным звеном 1-ого порядка или апериодическим звеном первого порядка. Это звено характеризуется двумя параметрами: коэффициентом усиления k и постоянной времени T.
Решением дифференциального уравнения (11) при нулевых начальных условиях и скачкообразном изменении входной величины от х=0 до х=1=const будет уравнение
y(t)=k (1 -  )(19)
)(19)
Это же уравнение можно записать в операторной (алгебраической) форме, которая позволяет вместо операций дифференцирования и интегрирования реальных функций времени (оригиналов) x(t), y(t) производить более простые алгебраические операции умножения и деления над операторными изображениями X(p) и Y(p) этих функций. При этом каждой функции времени должно однозначно соответствовать одно-единственное операторное изображение, не зависящее от времени – прямое преобразование Лапласа.
X(p) = 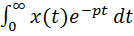 и Y(p) =
и Y(p) = 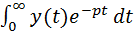 (20),
(20),
Где X(p) и Y(p) – изображения действительных функций времени;
P=s+jω – комплексная переменная, называемая оператором Лапласа, в которой s- действительная часть, jω- мнимая часть. При переходе от оригиналов к изображениям уравнение (14) примет вид:
TpY(p)+Y(p)=kX(p) или (Tp+1) Y(p)=kX(p)(21)
В установившемся режиме работы производные дифференциальных уравнений равны нулю (р=0) и решение уравнения (21) в операторной форме выглядит так:
Y(p)= 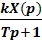 (22)
(22)
Так как передаточная функция звена W(p) – это отношение изображения выходной Y(p) величины звена к изображению входной величины X(p) при нулевых начальных условиях, то для инерционного звена она примет вид:
W(p)= 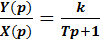 (23)
(23)
Знаменатель передаточной функции называют характеристическим полиномом. Если знаменатель прировнять нулю, то полученное уравнение называют характеристическим уравнением. Основное свойство инерционного звена Y(p)=W(p)*X(p) –операторное изображение выходной величины звена равняется передаточной функции звена, умноженной на изображение входной величины.
Переходная функция инерционного звена 1-ого порядка
(рисунок 28 а) совпадает с решением дифференциального
уравнения (13) при x(t)=1(t).

Рисунок 28
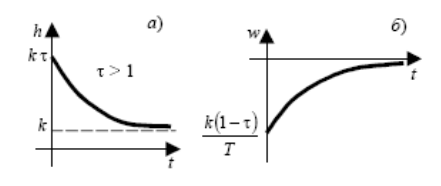
Рисунок 29
Передаточная функция инерционного звена 1-ого порядка приведена на рисунке 28, 29 (а).
Для нахождения временных характеристик звена надо определить его реакцию на единичное ступенчатое воздействие. Построим изображение переходной функции
H(p)= X(p)*W(p) =  *
* 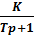 корни характеристического уравнения D(p)=p(Tp+1) = Tp2 + p = 0 (24)
корни характеристического уравнения D(p)=p(Tp+1) = Tp2 + p = 0 (24)
определяются как p1 = 0, p2 = -  .
.
Выполняя аналогичные преобразования над изображением весовой функции K(p) = W(p) получаем выражение для определения весовой функции
K(t) = 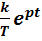 (25)
(25)
Весовая характеристика приведена на рисунке 28, 29 (б).
Примерами апериодических звеньев 1-ого порядка (инерционных) служат: емкость с самовыравниванием, контактный теплообменник, термопара и др.
Дата добавления: 2018-05-12; просмотров: 672; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
