IV. ОБЪЕКТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Общие понятия
Объектом управления могут быть поле, водоем, машина, агрегат и другие установки, производственными процессами в которых управляют устройства управления. Объектом химической технологии называется аппарат, система аппаратов, машина или другое устройство, в котором одна или несколько химико-технологических величин, характеризующих его состояние, поддерживаются автоматическими регуляторами на заданном значении или изменяются по определенному закону.
В химической промышленности объектами являются реакторы, абсорберы, экстракторы, ректификационные колонны, теплообменники, насосы, компрессоры и другие аппараты технологических установок, а также участки трубопроводов.
Являясь неотъемлемой частью АСУ или АСР, каждый объект представляет собой динамическую систему со своими входными и выходными величинами.К входным величинам относят регулирующие воздействия (потоки жидкостей, газов, тепловые потоки и т.д.), которые с помощью исполнительных устройств можно изменять, а также разнообразные возмущающие воздействия (изменение параметров исходного сырья и энергетических агентов, состояния технологического оборудования, атмосферных условий и т.д.).
В промышленных условиях автоматические системы, а так же их отдельные элементы, могут находиться в равновесных (статических) и неравновесных (динамических) состояниях. Равновесные состояния характеризуются постоянством во времени входных, промежуточных и выходных величин. При эксплуатации объектов химической технологии равновесные состояния систем нарушаются в результате действия различных возмущений, при этом входные, промежуточные и выходные величины систем изменяются во времени, что приводит их к неравновесному состоянию. Одним из существенных возмущений является изменение нагрузки объекта. Под нагрузкой объекта понимают количество вещества (тепла), которое проходит через объект в единицу времени.
|
|
|
Классификация объектов химической технологии
Как и системы управления, объекты могут быть одномерными и многомерными.
Одномерные объекты имеют одну выходную величину и описываются одним уравнением статики (1) и одним уравнением динамики (2).
Статическая модель содержит уравнение связи между входными и выходными величинами объекта в равновесном состоянии:
y=f(x,z) (1)
Динамическая модель связывает входные и выходные величины объекта в неравновесных состояниях:
Y=f(x, z, t) (2)
|
|
|
Графики, описывающие поведение объекта в установившемся режиме называются статическими характеристиками(рисунок 20).Здесь установившийся (статический) режим работы – это участки I и III, при котором характеристики системы не зависят от времени.
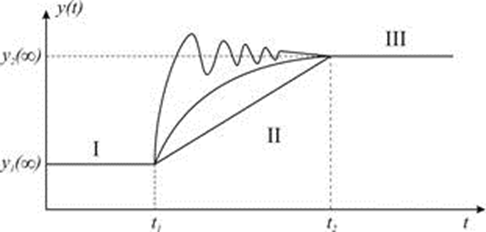
Рисунок 20
В многомерных объектах с независимыми выходными величинами изменение любой из входных величин приводит к изменению только своей выходной величины. Такие объекты можно разбить на несколько одномерных объектов и рассматривать их независимо один от другого.
В многомерных объектах с взаимозависимыми выходными величинами изменение входных величин приводит к одновременному изменению нескольких выходных величин, что объясняется наличием в таких объектах каналов перекрестных связей. Примером двухмерного объекта с перекрестными связями является экзотермический реактор идеального перемешивания.
Объекты могут обладать сосредоточенными и распределенными параметрами.
Объекты с сосредоточенными параметрами – это объекты, регулируемые величины которых имеют одно числовое значение в данный момент времени (уровень жидкости в аппарате, давление газа в газгольдере и др.). Динамика таких объектов описывается обыкновенными дифференциальными уравнениями с постоянными коэффициентами и начальными условиями.
|
|
|
Объекты с распределенными параметрами – это объекты, регулируемые величины которых (температура жидкости по длине теплообменника, концентрация компонентов по длине колонны и др.), имеют разные числовые значения в различных точках объекта в данный момент времени. Динамика объектов с распределенными параметрами описывается дифференциальными уравнениями в частных производных, дополненными начальными и граничными условиями. Поэтому при составлении математического описания объектов с распределенными параметрами их разбивают на ряд последовательно соединенных элементов с сосредоточенными параметрами, каждый из которых описывается обыкновенным дифференциальным уравнением. Точность такого описания тем выше, чем на большее число элементов был разбит исследуемый объект.
Математическое моделирование
Модель– это математическая копия реального объекта. Модель и оригинал должны быть похожи с некоторой вероятностью. В современной науке используются описательные (словесные), графические, табличные и другие модели. Мы будем изучать математические модели химико-технологических процессов (модели, выраженные в виде формул).
|
|
|
Начнем знакомство с основных «заповедей» математического моделирования:
1. Не решай сложную задачу, не решив простую – принцип простоты.
2. Без ошибки нет модели, а потому негрубые модели – плохие – принцип А.А. Андронова.
3. Можно пренебрегать чем угодно, нужно только точно знать, как это повлияет на результат – принцип Э. Хемингуэя.
4. Чем проще модель, тем реже она обманет – принцип надежности.
5. Точность результатов не может быть выше точности исходных данных; точности результатов промежуточных вычислений должны быть согласованы – принцип А.Н. Крылова
6. Цель расчетов – не числа, а понимание. Прежде чем решать задачу, подумай, что делать с ее решением – закон Р. Хемминга.
Началом и концом процесса математического моделирования является окружающая действительность. Последовательность действий при постановке задач математического описания объектов химической технологии начинается с нахождения уравнений его материального или энергетического балансов (за бесконечно малый промежуток времени dt).
Числовые величины, связанные с системой, делятся на переменные и параметры.
Параметры – это величины, которые можно считать постоянными в промежутке времени рассмотрения системы. Остальные числовые величины являются переменными. Значения переменных и параметров определяют количественную информацию о системе. Оставшаяся информация, качественная, определяет структуру системы. Выбор параметров определяется видом законов (зависимостей), которые применяются для описания.
Для объектов химической технологии нужно выявить кинетические закономерности, гидродинамические условия и т.п. В полученных уравнениях раскрывают значения неизвестных и исключают промежуточные переменные. Нелинейные дифференциальные уравнения, которым соответствуют непрерывные статические характеристики с большим радиусом кривизны, линеаризуют.
Линеаризацией называется замена нелинейных уравнений линеаризованными. Линеаризация возможна, если характер линеаризуемого уравнения не имеет разрывов и неоднозначностей. Линеаризация методом малых отклонений заключается в следующем.
Нелинейная функция переменных, характеризующих движение системы, имеет вид:
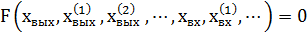(3)
Она раскладывается по степеням малых отклонений ее переменных от значений этих переменных для центра разложения, соответствующих исходному режиму движения в ряд Тейлора.
Для удобства пользования уравнения динамики обычно приводят к стандартному виду.
Если полученная модель окажется слишком сложной, ее надо разбить на несколько более простых подзадач – провести декомпозицию.
Обобщенная схема составления математической модели представлена на рисунке
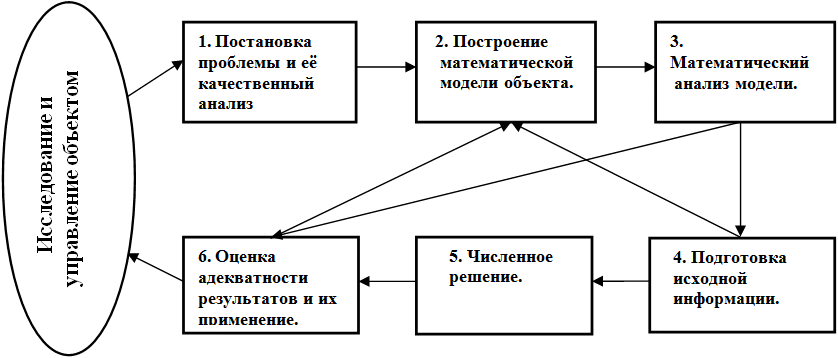
Рисунок 21
Любой объект взаимодействует с внешней средой с помощью входов и выходов. Входы – возможные воздействия на объект, выходы – те сигналы, которые можно измерить. Входы независимы, они приходят из внешней среды или от автоматического регулятора. При изменении информации на входе меняются и выходы.
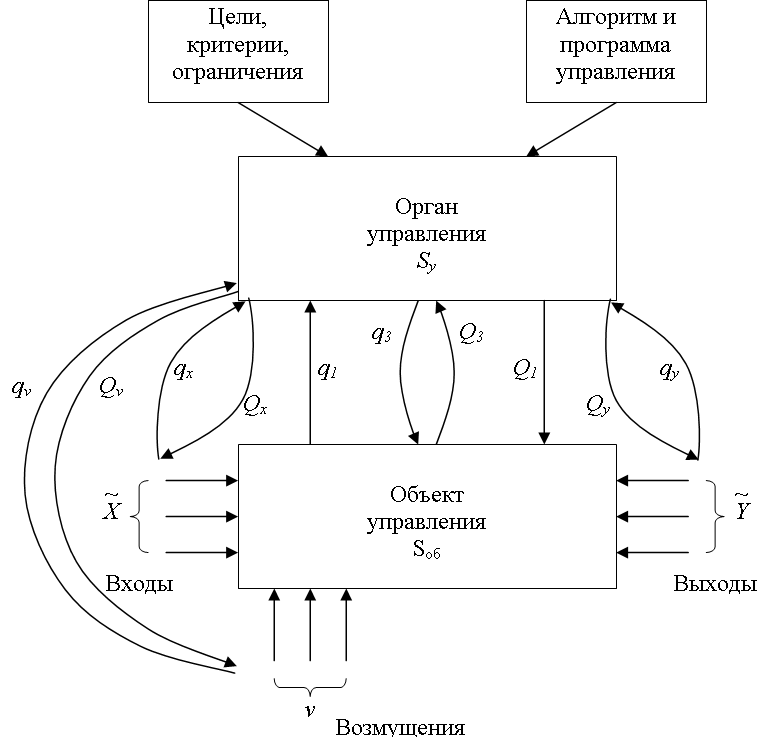
Рисунок 22
Существует некоторое правило, по которому элемент преобразует вход в выход. Это правило называется оператором и обозначается U[x]. Запись Y=U[x] означает, что выход получен в результате применения оператора U к входу х.
Построить модель – найти оператор. С его помощью можно предсказать реакцию объекта на любой входной сигнал.
Для любого технологического объекта управления можно построить множество моделей, которые будут учитывать (или не учитывать) те или иные факторы. На первом этапе стараются описать объект как можно подробней, но при этом бывает трудно теоретически рассчитать закон управления. Но даже если такой расчет возможен, то оказывается сложно это реализовать, или экономически невыгодно его реализовать. Можно упростить модель, отбросив некоторые маловажные, на взгляд разработчика, детали. Закон управления в таком случае получается проще, и часто с его помощью можно добиться желаемого результата, но нет гарантии, что реальная модель будет точно описывать процессы.
Чтобы составить математическое описание такой сложной системы ее разбивают на части, таким образом, чтобы каждая часть описывалась отдельным уравнением. Следовательно, необходимо иметь математическое описание ее отдельных элементов. Причем эти элементы выбираются так, чтобы они описывались дифференциальным уравнениям не выше второго порядка. Такие элементы системы называют типовыми звеньями. Совместно решая составленные для каждого звена уравнения, получают одно уравнение, описывающее весь процесс в целом. По этому уравнению и анализируют процессы в системе.
Метод математического моделирования значительно упрощает процесс исследования. Чтобы составить математическую модель достаточно знать математическое описание процессов в каждом звене, из которых состоит САУ.
Всем звеньям автоматики присущи следующие параметры:
1. Статическая и динамическая характеристика;
2. Передаточный коэффициент;
3. Погрешность;
4. Порог чувствительности.
Под статической характеристикой звена направленного действия понимают зависимость y=f(x), т.е. зависимость выходной величины от входной в установившемся режиме, когда x и yнеизменны во времени.
Динамическая характеристика описывает зависимость выходной величины yот входной величины x в переходном – динамическом – режиме, когда x и yменяются во времени.
Передаточный коэффициент звена представляет собой отношение выходной величины yк входной x . Различают статический передаточный коэффициент
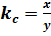и дифференциальный передаточный коэффициент, равный производной y по x , или (более грубо) отношению приращения функции к приращению аргумента.
= 
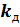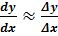, где ∆y= 
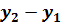, ∆x= 
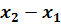(4)
Для линейной статической характеристики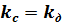 
при всех значениях x и y. Единица измерения передаточного коэффициента равна отношению единиц измерения выходной и входной величин. В практике пользуются относительным передаточным коэффициентом
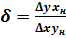,где 
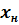и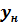 
номинальные значения входной и выходной величин. Для датчиков передаточный коэффициент называют коэффициентом чувствительности, а для усилителей – коэффициентом усиления.
Погрешностью называется разность между текущим и заданным значением выходной величины. Различают абсолютную и относительную погрешности, которые возникают вследствие изменений внутренних свойств элемента (износ, старение) и внешних условий (изменение температуры и влажности окружающей среды, изменение питающего напряжения и т. д.).
Порог чувствительности – наименьшее изменение входной величины, способное вызвать появление изменения выходной величины. Вызывается наличием в конструкциях элементов люфтов, трения, гистерезиса.
Тип звена определяется алгоритмом, в соответствии с которым происходит преобразование входного сигнала. Различают:
1. Пропорциональное (усилительное, безынерционное)
2. Апериодическое (инерционное) (электрическая цепь)
3. Интегрирующее 1-ого порядка (гидравлический исполнительный механизм)
4. Дифференцирующее 1-ого порядка
5. Колебательное 2-ого порядка (пневматические клапаны)
6. Запаздывающее (поточно-транспортные устройства)
Каждое звено характеризуется следующими динамическими характеристиками:
-Уравнение динамики.
-Передаточная функция.
-Переходной и весовой функциями.
-Частотными характеристиками.
Передаточная функция
Передаточная функция это математическое описание динамической системы.Уравнения динамики обычно решаются классическим методом или операционным методом, который основан на функциональном преобразовании Лапласа.
Классический метод применяют для решения дифференциальных уравнений движения, если их период не превышает трех, а так же если правая часть уравнения выражается простой функцией.
Операционный метод решения уравнений динамики состоит в следующем: исходное уравнение приводят к операторной форме, применяя преобразование Лапласа, с учетом заданных начальных условий. Затем решают полученное алгебраическое уравнение относительно искомой величины, записанной в операторной форме. И наконец, применяя оператор обратного преобразования, находят решение исходного уравнения динамики в обычной форме.
Уравнение динамики системы в операторной форме всегда проще исходного дифференциального уравнения.
Преобразование Лапласа основано на двух следующих формулах:
Дата добавления: 2018-05-12; просмотров: 1274; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!