Идеальное дифференцирующее звено.
Выходная величина идеального дифференцирующего звена является производной от входной величины. Дифференциальное уравнение имеет вид
(42)
Выполняя над этим уравнением преобразование Лапласа, получим выражение для передаточной функции идеального дифференцирующего звена
W(p) = kp(43)
Для нахождения временных характеристик определим его реакцию на единичное ступенчатое воздействие X(p)= 
.Таким образом, переходная характеристика
h(t) =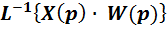 
= 
(44)
Примером идеального дифференцирующего звена может служить конденсатор, ток которого (выходная величина) является производной напряжения, приложенного к конденсатору (входная величина).
Рисунок 33
Реальное дифференцирующее звено можно представить, как последовательное соединение идеального дифференцирующего звена и инерционного звена первого порядка. Иногда реальное дифференцирующее звено называют инерционным дифференцирующим звеном. Переходная функция при воздействии единичного скачка выражается формулой
h(t) = 
(45)
Временные характеристики реального и идеального дифференцирующего звена представлены на рисунке 33.
Идеальное и реальное дифференцирующие звенья пропускают на выход только производную входной величины, но не пропускают саму величину. Поэтому в статическом режиме выходной сигнал дифференцирующего звена равен нулю.
Звено чистого запаздывания
Выходная величина в звене чистого запаздывания воспроизводит без искажения входную величину, но с фиксированным отставанием по времени. Часто это отставание характеризуется временем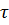 
транспортного запаздывания. Уравнение звена имеет вид:
|
|
|
(46)
Или в операторной форме:
(47)
Передаточная функция:
(48)
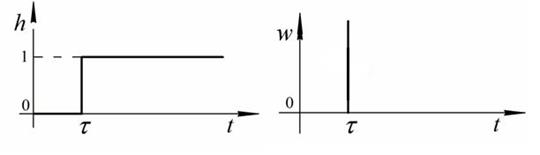
Рисунок 34
На рисунке 34(а) представлена переходная, а на 34(б) – весовая характеристики.
Основные сведения о типовых динамических звеньях представлены в таблице №3
Таблица №3
Процесс изменения регулируемой величины системы за все время ее работы называют процессом управления. В процессе управления различают переходные и установившиеся процессы.
V. Переходные процессы и их характеристики
Переходные процессы
Как и у всякой динамической системы, процессы в САУ делятся на установившиеся и переходные. При возникновении возмущающих или управляющих воздействий состояние равновесия в объекте нарушается и в нем возникает переходный процесс.
Переходным процессом называется изменение выходной величины во времени от момента нанесения возмущающего или задающего воздействиядо прихода ее в равновесное состояние. Переходный процесс зависит от динамических свойств системы, определяемых уравнением динамики, от входных воздействий и начальных условий. Переходный процесс y(t) имеет составляющую свободного движения 
, определяемую свойствами системы и начальными условиями, и составляющую вынужденного движения 
, определяемую свойствами системы и видом воздействия.
|
|
|
(49)
У разныхтиповых систем при одних и тех же возмущениях, в частности при нанесении на систему кратковременного возмущения переходные процессы протекают различно.Типовые переходные процессы: а - по заданию; б - по возмущению представлены на рисунке 35.
Различают следующие типовые переходные процессы:
колебательный (1), монотонный (2) и апериодический (3).
Рисунок 35
В переходном процессе регулируемая величина изменяется не совсем так, как изменилось возмущение, а по закону, который зависит от свойства всей системы регулирования. Если регулируемая величина изменяется плавно и не переходит через новое установившееся значение, а подходит к нему всегда с одной стороны, то процесс называется апериодическим. Если регулируемая величина приближается к своему новому установившемуся значению по колебательному закону, то процесс называется колебательным (затухающим или незатухающим).
|
|
|
При апериодическом сходящемся процессе (рисунок 36г) выходная величина плавно без колебания отклоняется от первоначального значения, и затем система постепенно возвращается в равновесное состояние. При колебательном сходящемся процессе, выходная величина совершает колебания с постепенно уменьшающейся амплитудой (рисунок 36 в).
При колебательном гармоническом процессе выходная величина совершает колебания с постоянной амплитудой (рисунок 36д). При колебательном расходящемся процессе – амплитуда колебаний выходной величины постепенно возрастает (рисунок 36б). Апериодический расходящийся процесс характеризуется непрерывным отклонением выходной величины системы от равновесного значения (рисунок 36а).
Рисунок 36
Установившийся режим системы, относительно которого рассматривается движение системы в процессе управления, называется исходным режимом.
Если воздействия после их приложения больше не изменяют своей величины, то в системе устанавливается статический режим.
Режим слежения с постоянной скоростью или режим установившихся колебаний выходной величины в устройстве являются не статическими, а установившимися.
|
|
|
Дата добавления: 2018-05-12; просмотров: 949; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!