Апериодическое звено 2-ого порядка (колебательное)
Колебательным называется звено, связь которого между функциями входа и выхода определяется дифференциальным уравнением 2-ого порядка.
Уравнение звена
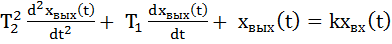(26)
Уравнение в операторной форме
(27)
Характеристическое уравнение звена
(28)
Имеем два корня
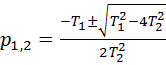(29)
Общее решение дифференциального уравнения, определяющее свободное движение (решения однородного дифференциального уравнения), имеет вид
(30)
Характер переходного процесса звена зависит от вида корней, которые могут быть действительными или комплексными числами.
Если Т1>2Т2, то корни характеристического уравнения будут действительными числами, которые можно представит в виде:
,
(31)
где Т3 и Т4 – некоторые условные постоянные времени, причем Т3>Т4.
Тогда динамическая характеристика звена имеет монотонный апериодический характер и звено называется апериодическим звеном второго порядка. Из уравнения (26) получается передаточная функция звена, знаменатель которой можно разложить на два множителя и представить передаточную функцию в следующем виде
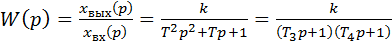(32)
где: 
; 
Из (30) следует, что инерционное звено второго порядка можно представить как последовательное соединение двух апериодических (инерционных) звеньев первого порядка с постоянными времени Т3 и Т4:
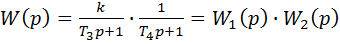(33)
где ; 
и 
Решение уравнения (26) с использованием условных постоянных времени Т3 и Т4 при нулевых начальных условиях и однократном ступенчатом воздействии хвх(t)=const имеет вид:
|
|
|
(34)
Временная характеристика (кривая разгона) представлена на рисунке 30(а) и 30(б) – функция веса.
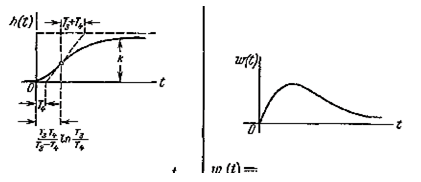
Рисунок 30
Частотные характеристики звена удобно получить из представления последовательного соединения двух апериодических звеньев первого порядка.
(35)
Если корни характеристического уравнения 30 – действительные отрицательные числа, то переходный процесс носит апериодический характер.Если корнями характеристического уравнения (28) являются сопряженные комплексные числа, то переходный процесс представляет собой затухающие колебания (рисунок 31а), а переходная характеристика определяется выражением:
(36)
Если же корнями характеристического уравнения (28)
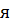вляются сопряженные мнимые числа, то переходный процесс носит колебательный характер без затухания (рисунок 31б) и переходная характеристика будет выглядеть следующим образом:
(37)
Рисунок 31
Примерами колебательных звеньев считают нагревательные и охладительные установки, отопительные печи, сушилки, теплицы и т.д.
Интегрирующее звено
Выходная величина этого звена является интегралом от входной величины. Дифференциальное уравнение в форме Коши:
|
|
|
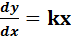(38)
или в интегральной форме
y = k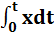 
(39)
Выполняя преобразование Лапласа, получим операторное уравнение:
pY(p)=kX(p)(40)
Отсюда получим выражение для передаточной функции интегрирующего звена.
W(p)= 
= 
(41)
Рисунок 32
Временные характеристики интегрирующего звена показаны на рисунке 32: а- переходная, б- весовая.
Примерами устройств, которые по динамическим характеристикам могут быть отнесены к интегрирующему звену, являются: емкость без самовыравнивания, паровой котел, гидравлический усилитель, любое механическое устройство, в котором входной величиной является скорость, в выходной – перемещение.
Дата добавления: 2018-05-12; просмотров: 975; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!