Глава 8. УЯВЛЕННЯ ПРО БУДОВУ АТОМА ВОДНЮ У КВАНТОВІЙ МЕХАНІЦІ
8.1. Схема розв’язку рівняння Шредінґера для атома водню. 8.2. Кутова частина рівняння Шредінґера. 8.3. Кутовий розподіл густини ймовірності знайти електрон в атомі водню. Електронна хмара. 8.4. Атомні орбіталі атому водню. 8.5. Фізичний зміст квантових чисел 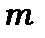 та l. 8.6. Просторове квантування. 8.7. Радіальна частина хвильової функції електрона атома водню. 8.8. Радіальний розподіл електронної хмари атома водню. 8.9. Квантові числа та їх фізичний зміст. 8.10. Правила відбору квантових чисел. 8.11. Висновки. 8.12. Контрольні запитання та вправи, тестові завдання. Література.
та l. 8.6. Просторове квантування. 8.7. Радіальна частина хвильової функції електрона атома водню. 8.8. Радіальний розподіл електронної хмари атома водню. 8.9. Квантові числа та їх фізичний зміст. 8.10. Правила відбору квантових чисел. 8.11. Висновки. 8.12. Контрольні запитання та вправи, тестові завдання. Література.
Схема розв’язку рівняння Шредінґера для атома водню
Атом водню складається із протона і електрона. Їх заряди 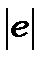 майже точкові порівняно з розмірами атома, тому що
майже точкові порівняно з розмірами атома, тому що 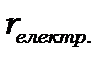 ,
, 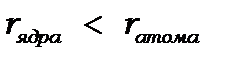 . Досліди Резерфорда показали, що між електроном і ядром діють кулонівські сили. Потенціал сил їх точкових зарядів має вигляд
. Досліди Резерфорда показали, що між електроном і ядром діють кулонівські сили. Потенціал сил їх точкових зарядів має вигляд
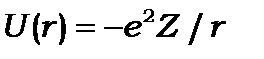 . (8.1)
. (8.1)
Маса ядра значно більша маси електрона 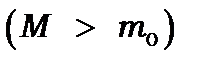 , тому в першому наближенні знехтуємо впливом скінченної маси ядра на рух електронів. Це дозволяє розглядати атом у системі координат, що зв’язана із центром атомного ядра. Скінчену масу ядра згодом можна буде врахувати, замінивши масу електрона
, тому в першому наближенні знехтуємо впливом скінченної маси ядра на рух електронів. Це дозволяє розглядати атом у системі координат, що зв’язана із центром атомного ядра. Скінчену масу ядра згодом можна буде врахувати, замінивши масу електрона 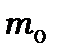 приведеною масою
приведеною масою 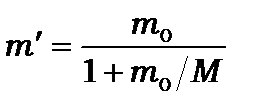 . Запишемо рівняння Шредінґера для стаціонарних станів атома водню
. Запишемо рівняння Шредінґера для стаціонарних станів атома водню
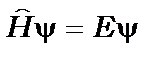 , (8.2)
, (8.2)
де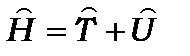 - оператор Гамільтона, що дорівнює
- оператор Гамільтона, що дорівнює
|
|
|
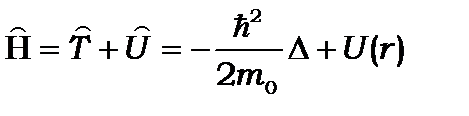 (8.3)
(8.3)
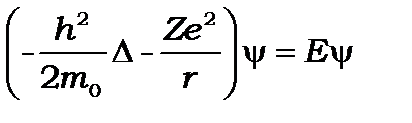 . (8.4)
. (8.4)
Оскільки потенціал 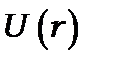 залежить лише від
залежить лише від 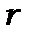 , тобто симетричний відносно центру, то зручно перейти у (8.4) до сферичних координат:
, тобто симетричний відносно центру, то зручно перейти у (8.4) до сферичних координат:
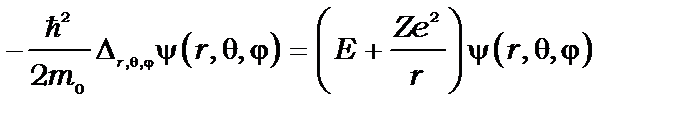 . (8.5)
. (8.5)
Тут
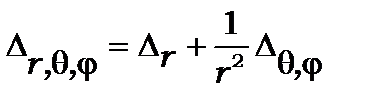 (8.6)
(8.6)
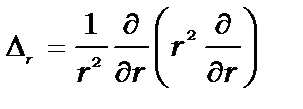 (8.7)
(8.7)
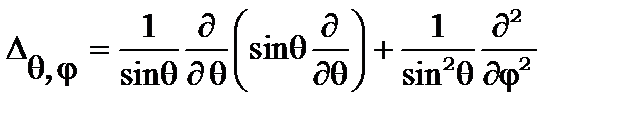 (8.8)
(8.8)
Підставивши (8.6…8.8) у (8.5), маємо
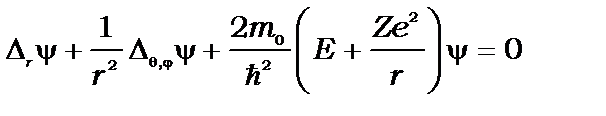 . (8.9)
. (8.9)
Помножимо ліву та праву частини рівняння (8.9) на 
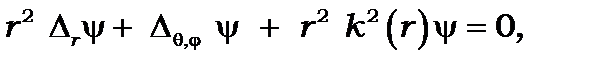 (8.10)
(8.10)
де 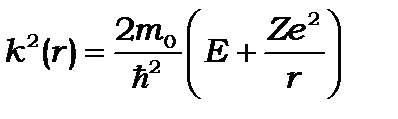 . (8.10*)
. (8.10*)
Розв’яжемо рівняння (8.10) методом розділення змінних. Для цього виберемо функцію 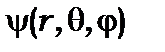 у вигляді добутку двох функцій
у вигляді добутку двох функцій
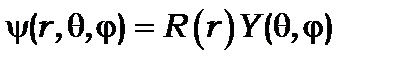 (8.11)
(8.11)
Підставимо (8.11) у (8.10) і помножимо обидві частини цього рівняння на 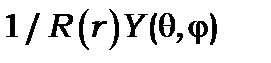
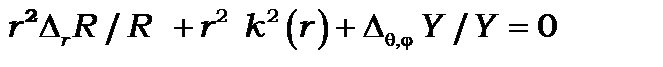 (8.12)
(8.12)
Рівняння (8.12) можна розділити на два рівняння, одне з яких залежить від 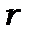 , а друге лише від
, а друге лише від 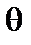 і
і 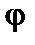 . Дійсно,
. Дійсно,
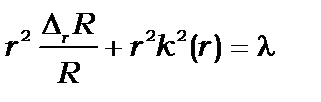 ` (8.13)
` (8.13)
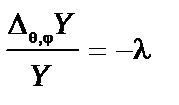 , (8.14)
, (8.14)
де 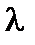 - довільна стала розділення.
- довільна стала розділення.
Проаналізуємо окремо кутову (8.14) й радіальну (8.13) частини рівняння Шредінґера.
|
|
|
Кутова частина рівняння Шредінґера
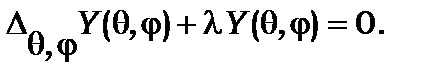 (8.14*)
(8.14*)
Рівняння (8.14) не залежить від 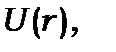 тому воно справедливе для будь-якого випадку кулонівського поля центральних сил.
тому воно справедливе для будь-якого випадку кулонівського поля центральних сил.
Його розв’язок є в довідниках і підручниках, тому обмежимося лише аналізом розв’язку. Насамперед методом розділення змінних знайдемо частину розв’язку, яка залежить лише від кута j. Для цього підставимо в (8.14) функцію 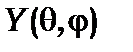 у вигляді добутку двох функцій
у вигляді добутку двох функцій 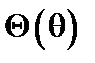 і
і 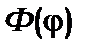
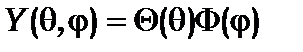 (8.15*)
(8.15*)
і помножимо ліву та праву частини (8.14*) на 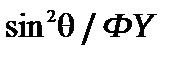 :
:
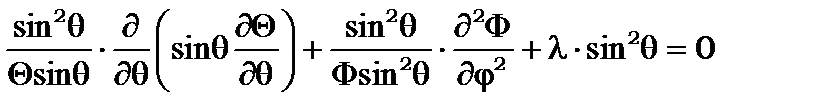 . (8.15)
. (8.15)
Рівняння (8.15) можна розділити на два рівняння, кожне з яких буде залежати лише від однієї змінної: одне - від 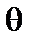 а друге - від
а друге - від 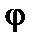
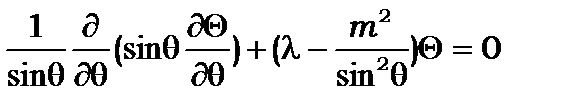 (8.16)
(8.16)
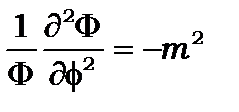 , (8.17)
, (8.17)
де 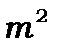 – стала розділення. Крім того у (8.16) і (8.17) частинні похідні можна замінити повними похідними, бо функції
– стала розділення. Крім того у (8.16) і (8.17) частинні похідні можна замінити повними похідними, бо функції 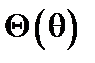 і
і 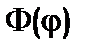 залежать лише від однієї змінної
залежать лише від однієї змінної 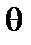 і
і 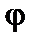 відповідно, а величина m може пробігати як позитивні, так і негативні значення.
відповідно, а величина m може пробігати як позитивні, так і негативні значення.
Окремий розв’язок (8.17) має вигляд
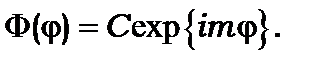 (8.18)
(8.18)
Його вигідно вибирати у такому вигляді ще й тому, що ця функція є власною функцією оператора проекції моменту кількості руху (8.37). Довільна стала С у (8.18) знаходиться за умови нормування
|
|
|
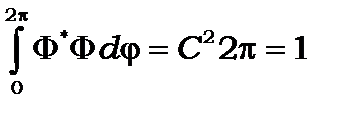 (8.19)
(8.19)
звідки
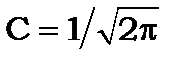 , (8.20)
, (8.20)
а функція 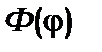 симетрична відносно осі
симетрична відносно осі 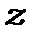 .
.
Хвильові функції повинні бути однозначними, неперервними та скінченними. За умови однозначності визначимо число m
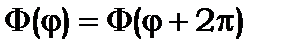 (8.21)
(8.21)
або 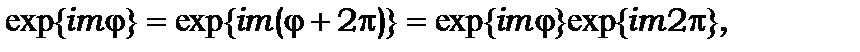 звідки число m може бути лише цілим числом:
звідки число m може бути лише цілим числом:
m = 0; ±1; ±2; ±3; ±4; ... (8.22)
Тепер проаналізуємо рівняння (8.16). Воно має скінченні, однозначні й неперервні розв’язки лише за таких значень роздільного параметра l, коли
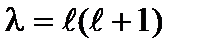 при
при 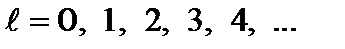 (8.23)
(8.23)
Розв’язок рівняння (8.16) має вигляд поліномів Лежандра
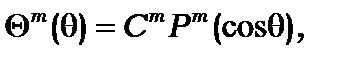 (8.24)[22]
(8.24)[22]
де 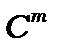 - нормуючі множники, що залежать, як і функціональні члени полінома Лежандра
- нормуючі множники, що залежать, як і функціональні члени полінома Лежандра 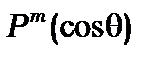 , від квантових чисел mі
, від квантових чисел mі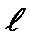 , де
, де
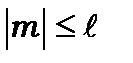 (8.25)
(8.25)
Коли 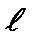 задано, число
задано, число 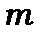 набуває
набуває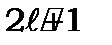 значень:
значень: 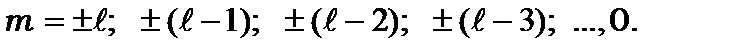
Наведемо приклади перших членів полінома Лежандра
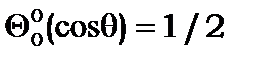
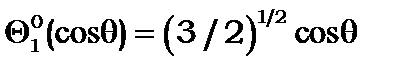
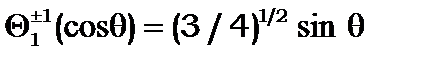
|
|
|
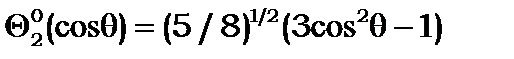
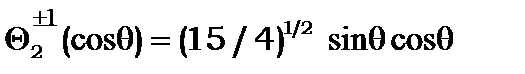
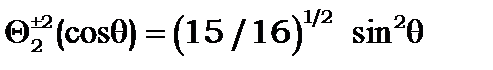 (8.26)
(8.26)
Вони є розв’язком рівняння (8.16), бо підстановка (8.26) у (8.16) перетворює рівняння (8.16) на тотожність.
Дата добавления: 2018-05-09; просмотров: 420; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
