Найпростіші випадки розв’язку рівнянь Шредінґера
7.2.1. Частинка в потенціальній ямі з нескінченними стінками
Розглянемо частинку в потенціальній ямі з нескінченими стінками, для якої потенціал 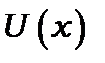 має вигляд:
має вигляд:
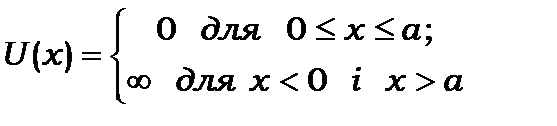 .
.
Розіб’ємо весь простір (одновимірна задача рис.7.1) на 3 області: 1 - 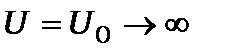 , 2 -
, 2 - 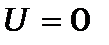 і 3 -
і 3 - 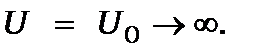 Для цих областей маємо 3-и рівняння:
Для цих областей маємо 3-и рівняння: 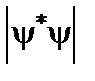
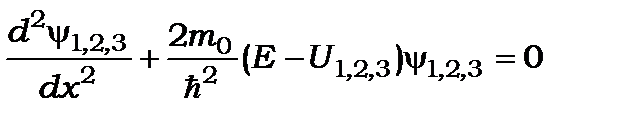 (7.10)
(7.10)
| Рис.7.1. Прямокутна потенціальна яма з нескінченими стінками. |
або 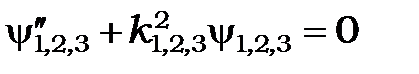 , (7.10*)
, (7.10*)
де 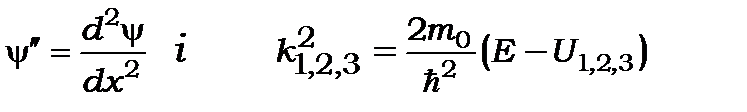 (7.11)
(7.11)
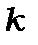 має розмірність см-1. Загальний розв’язок рівняння (7.10) має вигляд:
має розмірність см-1. Загальний розв’язок рівняння (7.10) має вигляд:
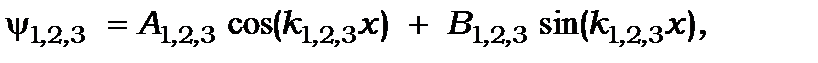 (7.12)
(7.12)
де А і В довільні сталі. Їх можна визначити з таких граничних умов:
1) в областях 1 і 2, де 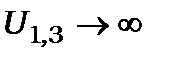 , частинка існувати не може, бо не може мати нескінчену енергію, звідки
, частинка існувати не може, бо не може мати нескінчену енергію, звідки 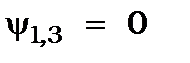 і
і 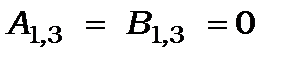 ;
;
2) умова неперервності хвильової функції дає
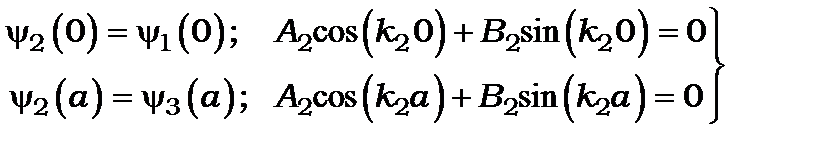 (7.13)
(7.13)
Із цих рівнянь знаходимо:
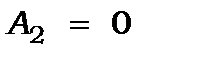 та
та  (7.13*)
(7.13*)
де 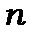 - ціле число, яке пробігає значення
- ціле число, яке пробігає значення 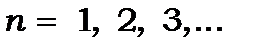
Підставимо в (7.13*) 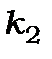 із формули (7.11), тоді
із формули (7.11), тоді 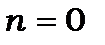
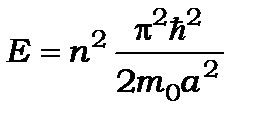 (7.14)
(7.14)
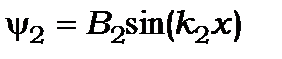 (7.15)
(7.15)
Проаналізуємо отримані результати.
· По-перше, енергетичний спектр частинки всередині потенціальної ями дискретний;
· По-друге, відсутній рівень із квантовим числом 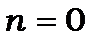 , бо це суперечить співвідношенню невизначеностей. Дійсно, якщо
, бо це суперечить співвідношенню невизначеностей. Дійсно, якщо 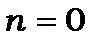 , то згідно (7.13),
, то згідно (7.13), 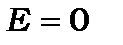 і
і 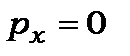 , а співвідношення невизначеності дає таке значення для
, а співвідношення невизначеності дає таке значення для 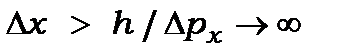 , що вимагає локалізації електрона у всьому просторі, а не в межах бар'єру;
, що вимагає локалізації електрона у всьому просторі, а не в межах бар'єру;
|
|
|
· По-третє, інтервал між дискретними рівнями енергії 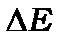 залежить від ширини потенціальної ями та квантового числа n
залежить від ширини потенціальної ями та квантового числа n
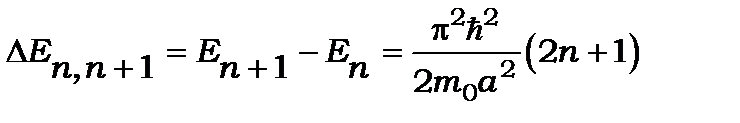 (7.16)
(7.16)
У таблиці 7.1 наведені дані для 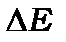 при різних
при різних 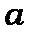 .
.
Таблиця 7.1. Значення  при різних а - ширина потенціальної ями
при різних а - ширина потенціальної ями
| а [Å] | 1 | 10 | 100 | 1000 |
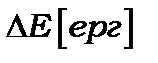
| 0,8´10-10 | 0,8´10-12 | 0,8´10-14 | 0,8´10-16 |
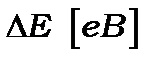
| 0,5´102 | 0,5 | 0,5´10-2 | 0,5´10-4 |
Експериментально виявити дискретні рівні енергії можливо лише тоді, коли 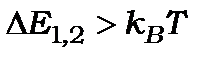 . Для
. Для 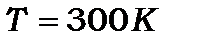 і
і 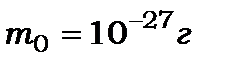
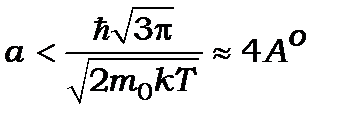
Ці квантові властивості твердого тіла малих розмірів дійсно спостерігаються експериментально й називаються квантовим розмірним ефектом, який останнім часом знайшов застосування в наноелектроніці.
· По-четверте, під час переходу з одного стаціонарного стану з енергією 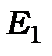 в інший з енергією
в інший з енергією 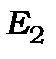 відбувається поглинання або випромінювання кванта енергії
відбувається поглинання або випромінювання кванта енергії 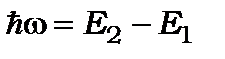 .
.
Частинка в потенціальній ямі зі скінченними стінками
У випадку потенціальної ями зі стінками скінченої висоти розв’язок задачі знаходиться так, як і для ями з нескінченими стінками. (див. задачу №2, розділ 5 [1]).
Ця задача буде розв’язуватись на практичних заняттях. Результати розв’язку такі:
· По-перше, частинки мають при 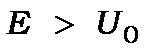 неперервний спектр енергії, як і у вільної частинки.
неперервний спектр енергії, як і у вільної частинки.
|
|
|
· По-друге, при 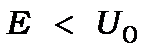 спектр енергії частинки дискретний і для найглибших рівнів збігається з попереднім випадком ями з нескінченими стінками.
спектр енергії частинки дискретний і для найглибших рівнів збігається з попереднім випадком ями з нескінченими стінками.
· По-третє, не існує рівня енергії із квантовим числом 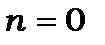 , тому що це суперечить співвідношенню невизначеностей.
, тому що це суперечить співвідношенню невизначеностей.
· По-четверте, на відміну від попереднього випадку ями з нескінченими стінками для ями зі скінченими стінками хвильові функції не прямують до нуля на його стінках, а плавно (експоненціально) затухають у середині стінки ями, як це показано на схематичному рис.7.2.
| Рис.7.2. Потенціальна яма зі скінченими стінками: а – хвильові функції для |
Гармонічний осцилятор
Потенціальна енергія гармонічного осцилятора є парабола 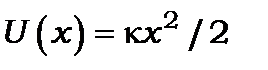 , де
, де 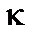 - коефіцієнт квазіпружної сили
- коефіцієнт квазіпружної сили 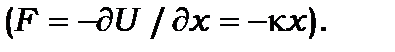 Одновимірне рівняння Шредінґера для стаціонарних станів має такий вигляд:
Одновимірне рівняння Шредінґера для стаціонарних станів має такий вигляд:
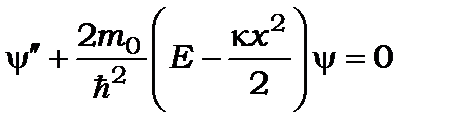 . (7.17)
. (7.17)
де m0 – маса частинки. Пам’ятаючи, що в попередньому випадку частинки в потенціальній ямі ми отримали дискретний спектр енергії, можна очікувати, що й у цьому випадку матимемо також дискретний спектр енергій, хоча залежність від квантових чисел і параметрів осцилятора буде іншою. Хвильова функція між класичними точками повороту (точками на кривій 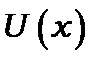 ) має вигляд осцилюючої функції, а зовні вона експоненціально затухає. Відповідність із класичним осцилятором спостерігається при
) має вигляд осцилюючої функції, а зовні вона експоненціально затухає. Відповідність із класичним осцилятором спостерігається при 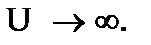
|
|
|
| Рис.7.3. Параболічна потенціальна яма, |
Розв’язок рівняння Шредінґера дає таку залежність для власних значень енергії осцилятора:
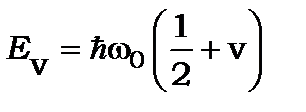 (7.18)
(7.18)
де  - вібронне (коливальне) квантове число, котре пробігає значення
- вібронне (коливальне) квантове число, котре пробігає значення 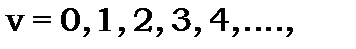 а
а 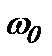 - власна частота гармонічного осцилятора
- власна частота гармонічного осцилятора
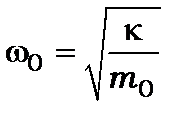 (7.19)
(7.19)
Нульову енергію осцилятора 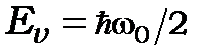 можна знайти, користуючись співвідношенням невизначеностей
можна знайти, користуючись співвідношенням невизначеностей 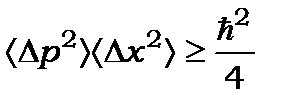 та ще й умовою мінімуму повної енергії гармонічного осцилятора
та ще й умовою мінімуму повної енергії гармонічного осцилятора 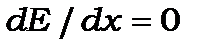 . Дійсно,
. Дійсно, 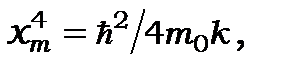 тоді
тоді 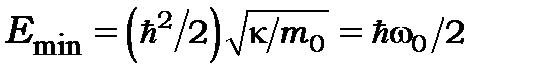 . Аналізуючи рис.7.3, на якому схематично зображені енергетичні рівні, хвильові функції і квадрати хвильових функцій для різних вібронних (коливальних) квантових чисел
. Аналізуючи рис.7.3, на якому схематично зображені енергетичні рівні, хвильові функції і квадрати хвильових функцій для різних вібронних (коливальних) квантових чисел 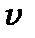 , зробимо такі висновки:
, зробимо такі висновки:
· дискретний спектр енергій гармонічного осцилятора лінійно залежить від вібронного (коливального) квантового числа 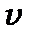 ;
;
|
|
|
· можливий стан із квантовим числом 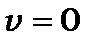 , енергія якого рівна
, енергія якого рівна 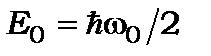 ;
;
· інтервал енергій між двома стаціонарними станами рівний 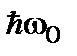 ;
;
· імовірність знайти електрон у певному стані залежить від вібронного числа 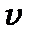 . При малих значеннях квантового числа
. При малих значеннях квантового числа 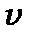 квантовий осцилятор найбільш суттєво відрізняється від класичного. Найбільша густина ймовірності знайти електрон квантового осцилятора
квантовий осцилятор найбільш суттєво відрізняється від класичного. Найбільша густина ймовірності знайти електрон квантового осцилятора 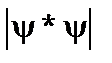 знаходиться в точках, розташованих ближче до точки
знаходиться в точках, розташованих ближче до точки 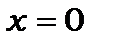 (рис.7.3), тоді як для класичного осцилятора вона знаходиться в станах на кривій
(рис.7.3), тоді як для класичного осцилятора вона знаходиться в станах на кривій 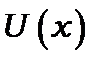 , коли його кінетична енергія
, коли його кінетична енергія 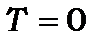 ; чим більше квантове число
; чим більше квантове число 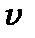 , тим більша ймовірність знайти осцилятор в стані з нульовою кінетичною енергією, тобто знайти його в стані на кривій
, тим більша ймовірність знайти осцилятор в стані з нульовою кінетичною енергією, тобто знайти його в стані на кривій 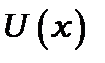 ;
;
· треба також пам’ятати, що з усіх можливих переходів між стаціонарними станами спостерігаються ті, для яких виконується таке правило відбору. 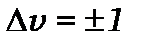
На закінчення зауважимо, що гармонічний осцилятор дуже важливий фізичний об’єкт згідно теореми про нормальні координати систему в нормальних координатах розглядають як набір гармонічних осциляторів. За його допомогою вдається зрозуміти закони теплового випромінювання, сили Ван-дер-Ваальса, коливальні спектри молекул тощо.
Дата добавления: 2018-05-09; просмотров: 398; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

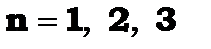 ,
, 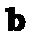 – модуль квадрата хвильової функції.
– модуль квадрата хвильової функції.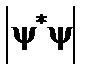 (суцільні криві), пунктир – класична ймовірність знайти електрон у коливному стані, вставка – зменшене зображення
(суцільні криві), пунктир – класична ймовірність знайти електрон у коливному стані, вставка – зменшене зображення 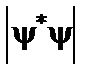 для
для 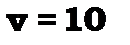 .
.